Лабораторная работа № 7
Синтез оптимальных следящих систем (краткие теоретические сведения)
Постановка задачи
Задача следящей системы – отслеживать на выходе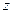 
сигнал 
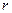, подаваемый на вход. Например, систему автоматического управления курсом корабля (автопилот) можно рассматривать как следящую систему ( 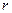– заданный курс, 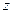– фактический курс).
Точность следящей системы определяется свойствами сигнала ошибки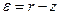 
:
Если эталонный (задающий) сигнал 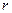– случайный процесс с известной спектральной плотностью, мы получаем задачу оптимизации при случайных возмущениях, варианты которой были рассмотрены ранее.
Здесь мы остановимся на задаче оптимизации при детерминированных (известных, определенных, неслучайных) возмущениях. Это означает, что мы знаем входной сигнал 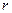(например, его изображение по Лапласу 
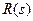). При этом требуется обеспечить «малость» ошибки 
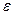в некотором смысле. В идеальном случае ошибка равна нулю для любого момента времени. В реальных системах этот результат чаще всего недостижим, поскольку требует бесконечно большого управления.
Предположим, что входной сигнал имеет ступенчатый вид, причем можно считать, что его изменение происходит достаточно редко, так что при очередном скачке переходный процесс, вызванный предыдущим изменением, уже закончился. В этом случае имеет смысл строить оптимальную систему для единичного скачка на входе. Так как система линейная, при любом изменении величины скачка она останется оптимальной (изменится только величина сигналов).
В идеале мы хотим, чтобы изменение входного сигнала мгновенно привело к такому же изменению на выходе. Можно догадаться, что для мгновенного перевода инерционной системы (а не просто усилителя) в новое состояние требуется бесконечное управление. Этот вариант неприемлем с практической точки зрения и нереализуем, поскольку управляющий сигнал всегда ограничен. Таким образом, реальный переходный процесс будет отличаться от идеального. Как же измерить эту ошибку, оценив ее одним числом?
| 
|
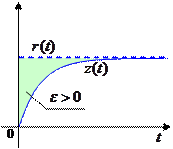
Казалось бы, можно взять интеграл от сигнала ошибки 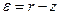на интервале от 0 до бесконечности[1]
,
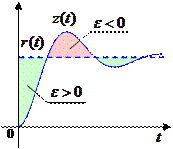
однако он может служить для оценки ошибки только при монотонном переходном процессе, когда ошибка всегда остается положительной (см. рисунок слева). Если процесс колебательный, на разных интервалах ошибка может принимать как положительные, так и отрицательные значения, поэтому использовать этот интеграл для оценки ошибки нельзя (см. рисунок справа).
Мы можем справиться с этой проблемой, если интегрировать модуль ошибки:
.
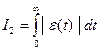Такую оценку иногда используют при численной оптимизации. К сожалению, получить оптимальную передаточную функцию регулятора аналитически (по формулам) в этом случае не удается.
Удобнее всего минимизировать интеграл от квадрата ошибки (его также называют интегральной квадратической ошибкой):
.
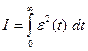(24)
Далее мы увидим, что задачу оптимизации по такому критерию удается свести к задаче фильтрации Винера.
Теорема Парсеваля
Для большинства задач в теории управления существует два типа решений – временное (когда рассматривается изменение сигналов во времени) и частотный (работа с передаточными функциями и частотными характеристиками).
Эти подходы не исключают, а взаимно дополняют друг друга, позволяя увидеть разные стороны одной задачи. Для построения оптимального фильтра Винера мы использовали операции с передаточными функциями (частотный метод Боде и Шеннона), хотя сам Винер впервые предложил решение этой задачи с помощью временного метода (на основе корреляционных функций).
Для того, чтобы использовать уже рассмотренные алгоритмы, нужно «перевести» задачу с критерием (24) в частотную область, то есть, выразить критерий через изображения сигналов по Лапласу и передаточные функции. Это позволяет сделать теорема Парсеваля, которая утверждает, что интеграл от квадрата функции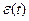 
, которая равна нулю при 
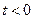и стремится к нулю при 
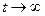, равен интегралу от «квадрата» ее преобразования Лапласа 
:
.
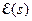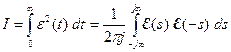(25)
Выражение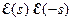 
можно назвать «квадратом» потому что оно на мнимой оси (где берется интеграл), при подстановке 
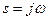, действительно является квадратом частотной характеристики 
:
.
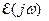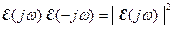Заметим, что функционал (25) в нашей задаче (при известном входном сигнале) совпадает по форме (при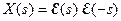 
) с функционалом (13), который получен в задаче фильтрации при случайных возмущениях. Поэтому для решения задачи можно использовать алгоритм, применявшийся при расчете фильтра Винера.
Эквивалентность двух задач
Теорема Парсеваля позволяет обнаружить связь между задачами анализа и синтеза при случайных (или стохастических) и детерминированных возмущениях.
Поскольку ошибка 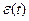стремится к нулю при 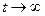, ее преобразование Лапласа 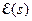– устойчивая функция (все ее полюса имеют отрицательные вещественные части). Если рассматривать 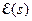как передаточную функцию формирующего фильтра, то можно построить соответствующую спектральную плотность 
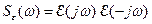, так что
.
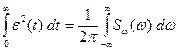Таким образом, интеграл от квадрата функции 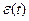, стремящейся к нулю при 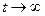, равен среднему квадрату случайного процесса, имеющего спектральную плотность 
.
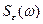Пусть существует некоторая система с передаточной функцией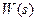 
. Обозначим ее входной сигнал через 
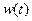, а выходной – через .
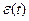Если 
– единичный центрированный белый шум, то спектральная плотность выхода равна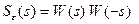 
, а дисперсия выхода (средний квадрат) – интегралу от спектральной плотности по мнимой оси.
В то же время, если 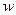– единичный импульс (дельта-функция), изображение выхода по Лапласу равно 
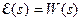, а интегральная квадратическая ошибка равна тому же самому интегралу от 
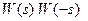. Таким образом, вместо вычисления дисперсии выхода при белом шуме на входе можно вычислить интеграл от квадрата выходного сигнала при импульсном входе, и наоборот. Квадратный корень из этой величины называется 
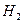-нормой передаточной функции :
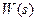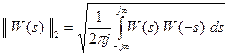
и вычисляется с помощью функции norm среды Matlab.
С другой стороны, пусть передаточная функция 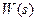зависит определенным образом от выбора регулятора 
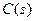. Тогда, как следует из сказанного, две следующие задачи оптимизации эквивалентны:
1) найти регулятор 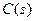, минимизирующий дисперсию ошибки при единичном белом шуме на входе;
2) найти регулятор 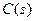, минимизирующий интегральную квадратическую ошибку при поступлении на вход единичного импульса (дельта-функции).
Вторая задача в теории управления называется задачей 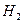-оптимизации или просто 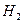-задачей (поскольку требуется обеспечить минимум 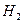-нормы передаточной функции замкнутой системы), а о первой говорят как о стохастическом варианте 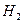- задачи.
Разомкнутые системы
Чтобы понять особенности задачи, сначала мы рассмотрим простейшую разомкнутую систему, состоящую только из регулятора 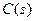и объекта 
:
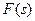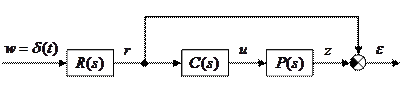
Входной сигнал 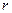задан в виде преобразования Лапласа 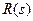, так что его можно представить как результат прохождения единичного импульса (дельта-функции 
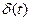) через звено с передаточной функцией 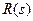. Такой способ общепринят при моделировании входных сигналов и позволяет представить систему в стандартном виде: на входе – дельта-функция, на выходе – ошибка.
Передаточная функция системы от входа 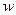к выходу 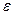равна
.
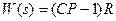Предполагается, что все звенья устойчивы. Это значит, что все полюса функци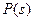й 
и 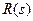имеют отрицательные вещественные части и регулятор 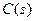, который требуется найти, также должен обладать этим свойством. Кроме того, регулятор должен обеспечить минимум интегральной квадратической ошибки
,
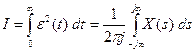где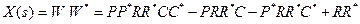 
. Подынтегральное выражение имеет форму ( 12 ), как для задачи Винера, поэтому можно применить уже известный алгоритм поиска оптимальной устойчивой передаточной функции .
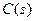Попытаемся понять, какие результаты мы можем получить в результате оптимизации. Прежде всего, выбор регулятора из условия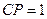 
сразу дает 
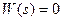, то есть, ошибка будет нулевой не только при ступенчатом, но и при любом другом входе. Это так называемое условие инвариантности, при котором обеспечивается идеальное слежение за эталонным сигналом. Именно такой регулятор будет получен в результате оптимизации «в лоб».
К сожалению, все не так просто. Как правило, передаточные функции реальных объектов – строго правильные, то есть, степень их числителя меньше, чем степень знаменателя. Тогда передаточная функция регулятора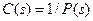 
будет неправильной (степень числителя больше степени знаменателя). Как было показано при анализе задачи оптимизации при случайных возмущениях, такой регулятор неприменим в практических задачах по двум причинам:
1) регулятор содержит дифференцирующее звено, поэтому при скачкообразном изменении входного сигнала сигнал управления должен теоретически стать бесконечным;
2) регулятор усиливает высокочастотные помехи измерений вместо того, чтобы подавлять их; это делает систему неработоспособной.
В задаче оптимизации при случайных возмущениях мы добивались «ската» частотной характеристики регулятора на высоких частотах с помощью ограничения на сигнал управления: в критерий качества вводилась дисперсия управления с некоторым весовым коэффициентом, который подстраивался методом проб и ошибок.
Если формально составить критерий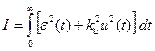 
, добавив интеграл от квадрата сигнала управления 
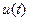с весовым коэффициентом 
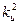, то ничего хорошего не получится, поскольку установившееся значение 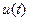при 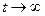не равно нулю. Следовательно, интеграл расходится и теорема Парсеваля неприменима. Оптимизация в частотной области не имеет смысла: если формально применить алгоритм синтеза, получится регулятор, для которого ошибка в установившемся режиме (при 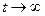) не равна нулю.
Чтобы грамотно ограничить управляющий сигнал, нужно ввести ошибку управления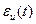 
, то есть отклонение фактического сигнала управления 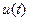от некоторого эталонного сигнала 
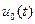, который должен быть выбран так, чтобы функция 
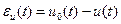стремилась к нулю при 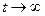. Тогда можно искать минимум критерия
,
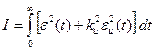это позволит ограничить мощность управления и при этом минимизировать ошибку слежения. Изменяя коэффициент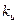 
, мы получим семейство Парето-оптимальных регуляторов, как и в задаче оптимизации при случайных возмущениях.
Как же выбрать сигнал 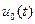? Для простоты рассмотрим только случай ступенчатого входного сигнала. Поскольку передаточная функция 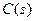устойчива, установившееся значение 
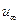сигнала 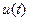при 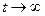– постоянная величина, ее можно рассчитать следующим образом.
Если вход 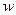– это единичный импульс, то установившееся значение эталонного сигнала 
можно определить по теореме о конечном значении для преобразования Лапласа
.
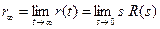Например, если – единичный ступенчатый сигнал, для которог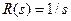о 
, то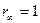 
. С другой стороны, для того, чтобы установившаяся ошибка была равна нулю, необходимо, чтобы предельное значение сигнала 
тоже было равно 
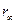. Учитывая, что 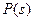– устойчивая передаточная функция, имеем
,
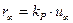где 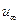– нужное нам установившееся значение сигнала управления, а 
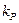– статический коэффициент усиления объекта, который вычисляется по формуле 
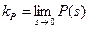(в среде Matlab это делает функция dcgain). Таким образом, в качестве эталонного сигнала управления можно выбрать любой сигнал 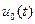, у которого предельное значение при 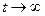равно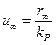 
, например, ступенчатый сигнал 
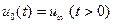, изображение которого равно 
.
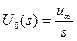Теперь построим стандартную систему, соответствующую задаче оптимизации. Уравнения в изображениях имеют вид:
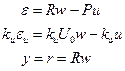
Учитывая, что первые два уравнения определяют ошибки по выходу и по управлению, имеем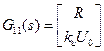 
, 
, 
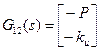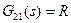и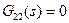 
.
Замкнутые системы
Теперь рассмотрим аналогичную задачу для замкнутой системы.
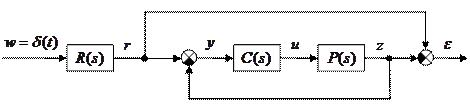
Что изменилось с появлением замкнутого контура? Во-первых, уже не требуется, чтобы передаточные функции регулятора 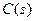и объекта 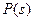были устойчивыми. Во-вторых, требуется обеспечить устойчивость замкнутой системы. В-третьих, поскольку 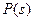может содержать множитель 
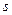в числителе (соответствующий интегрирующему звену), статический коэффициент усиления 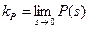может оказаться равным бесконечности. Поэтому нужно скорректировать процедуру выбора эталонного управляющего сигнала.
Передаточная функция от входа 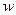к ошибке 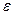равна
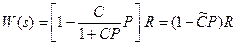, где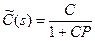 
,
поэтому подынтегральное выражение в критерии качества будет зависеть от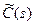 
, а не от 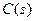. Чтобы обеспечить устойчивость получаемой оптимальной системы в общем случае нужно использовать параметризацию стабилизирующих регуляторов (см. аналогичную задачу при случайных возмущениях).
При определении эталонного сигнала управления вроде бы все осталось по-прежнему: по теореме о предельном значении
.
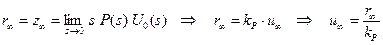Однако, проблема в том, что объект может содержать интегрирующие звенья, поэтому статический коэффициент усиления 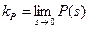обращается в бесконечность. В этом случае эталонный сигнал управления должен стремиться к нулю при 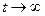. Например, можно принять 
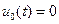при всех 
.
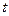Построим стандартную систему в задаче оптимизации по критерию
.
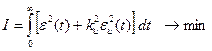Уравнения системы имеют вид
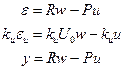
Учитывая, что первые два уравнения определяют ошибки по выходу и по управлению, имеем 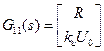, , 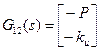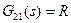и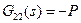 
. Как видим, все отличие от разомкнутой системы состоит в функции 
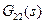, которая в данном случае не равна нулю и представляет собой передаточную функцию контура (без регулятора).
Можно показать, что устойчивые полюса передаточной функции объекта 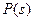(и неустойчивые полюса, «отраженные» от мнимой оси) становятся корнями характеристического уравнения оптимальной замкнутой системы. Вроде бы получается, что для объекта, включающего интегрирующее звено, задача не имеет решения. Однако из этого правила есть исключение: если модель входного сигнала 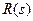также содержит интегрирующее звено (например, для единичного ступенчатого сигнала 
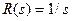), в ходе синтеза происходит сокращение двух множителей и оптимальная система оказывается устойчивой.
Если учитывать динамику привода и датчиков, схема немного усложняется:
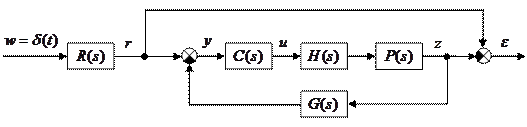
В этом случае стандартная система описывается матрицам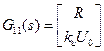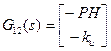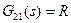и
, 
, и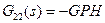 
.
[1] Чтобы такой интеграл сходился, необходимо, чтобы ошибка стремилась к нулю при.