Рекурсия
Методические указания к лабораторной работе № 8
«Основы алгоритмизации и программирования»
Ростов-на-Дону
Составитель: С.В.Шинакова
Методические указания и задания к выполнению лабораторной работы по теме "Программирование в Delphi: введение Object Pascal" / ДГТУ, Ростов-на-Дону, 2009. ** с.
Излагаются теоретические и технологические сведения, необходимые для создания консольных приложений в Delphi. Целью работы ставится выработка навыков программирования при помощи современных визуальных средств.
Рецензент:
Печать оперативная. Формат 60х84/16. Бумага офсетная.
Объем 0,7 усл.-п.л., 0,7 уч.-изд.л.
Тираж ** экз.
__________________________________________________
ã ДГТУ, 2009
Цель работы
Цель работы сводится к изучению рекурсивных подпрограмм. В данной работе рассматривается рекурсия и функции работы с ними.
Рекурсивные подпрограммы
Рекурсивной называется подпрограмма, в которой содержится обращение к самой себе. Такая рекурсия называется прямой. Есть также косвенная рекурсия, когда две или более подпрограмм вызывают друг друга.
При обращении подпрограммы к самой себе происходит то же самое, что и при обращении к любой другой функции или процедуре: в стек записывается адрес возврата, резервируется место под локальные переменные, происходит передача параметров, после чего управление передается первому исполняемому оператору подпрограммы. При повторном вызове этот процесс повторяется. Ясно, что для завершения вычислений каждая рекурсивная подпрограмма должна содержать хотя бы одну нерекурсивную ветвь алгоритма, заканчивающуюся возвратом в вызывающую программу.
При завершении подпрограммы область ее локальных переменных освобождается, а управление передается на оператор, следующий за рекурсивным вызовом.
Простой пример рекурсивной функции — вычисление факториала (это не означает, что факториал следует вычислять именно так). Чтобы получить значение факториала числа n, требуется умножить на n факториал числа
(n-1). Известно также, что 0! = 1 и 1! = 1.
function fact(n: byte): longint:
begin
if (n = 0) or (n = 1) then fact:= 1
else fact:= n * fact(n - 1);
end;
Рассмотрим, что происходит при вызове этой функции при n = 3. В стеке отводится место под параметр n, ему присваивается значение 3, и начинается выполнение функции. Условие в операторе if ложно, поэтому управление передается на ветвь else. Для вычисления выражения n*fact(n-1) требуется повторно вызвать функцию fact. Для этого в стеке отводится новое место под параметр n, ему присваивается значение 2, и выполнение функции начинается сначала. В третий раз функция вызывается со значением параметра, равным 1, и вот тут-то становится истинным выражение (n = 0) оr (n - 1), поэтому происходит возврат из подпрограммы в точку вызова, то есть на выражение n*fact(n-1) для n=2. Результат выражения присваивается имени функции и передается в точку ее вызова, то есть в то же выражение, только теперь происходит обращение к параметру n, равному 3.
Понимание механизма рекурсии помогает осознать ее достоинства, недостатки и область применения.
Рекурсивные подпрограммы чаще всего применяют для компактной записи рекурсивных алгоритмов, а также для работы со структурами данных, описанными рекурсивно, например с двоичными деревьями. Любую рекурсивную функцию можно реализовать без применения рекурсии: для этого программист должен сам обеспечить распределение памяти под необходимое количество копий параметров.
Достоинством рекурсии является компактная запись. К недостаткам относятся расход времени и памяти на повторные вызовы функции и передачу ей параметров, а главное, опасность переполнения стека.
При отладке рекурсивных алгоритмов полезно отслеживать глубину рекурсии либо визуально, вставив оператор вывода в начало подпрограммы, либо с помощью типизированной константы, которая увеличивается на единицу при каждом вызове подпрограммы, например:
function fact(n: byte): longint;
const num: word = 0;
begin
inc(num);
writeln(num); { отладочная печать }
if (n = 0) or (n = 1) then fact:= 1
else fact:= n * fact(n - 1);
end;
Напомню, что локальная типизированная константа, в отличие от локальной переменной, размещается в сегменте данных и сохраняет свое значение между вызовами подпрограммы.
В случае переполнения стека программа завершится с соответствующим сообщением об ошибке. Проверка переполнения стека задается ключом компилятора {$S+}. По умолчанию он включен.
Задачи
1. Напишите рекурсивную функцию для нахождения биномиальных коэффициентов (для заданного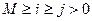 
вычислите все 
):
2. Напишите рекурсивную функцию, которая по заданным вещественному x и целому n вычисляет величину xn согласно формуле:
Теоретические вопросы
1. Как называются процедуры или функции, которые вызывают сами себя?
2. Для каких целей создаются рекурсивные алгоритмы?
3. Что называется стеком?
4. Верно ли, что значения всех локальных переменных при очередном вызове рекурсивной процедуры или функции помещаются в стек?
5. В какой последовательности происходит заполнение стека и выбор элементов из стека?
6. Всегда ли в рекурсивном алгоритме должно присутствовать условие выхода из рекурсии?
7. Что произойдет, если рекурсивный алгоритм будет вызывать сам себя «бесконечное» число раз?
8. Верно ли, что решение задачи, реализуемое рекурсивным алгоритмом, можно выразить нерекурсивным алгоритмом?
Задания для самостоятельной работы
1. По заданным границам интегрирования а и b вычислите значение определенного интеграла следующего вида:
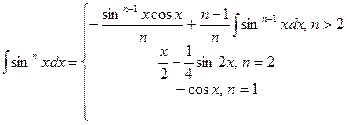
10. 