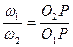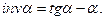ЗУБЧАТЫЕ ПЕРЕДАЧИ
5.1. Общие положения
Зубчатые передачи предназначены для передачи вращательного движения от одного вала к другому, а также для изменения величины и направления угловой скорости валов. Пара зубчатых колес, находящихся в зацеплении друг с другом, называется ступенью. Такие передачи называют одноступенчатыми.
По характеру расположения валов все зубчатые одноступенчатые передачи можно разделить на цилиндрические, конические и гиперболоидные.
В цилиндрических передачах (рис. 5.1а) оси валов параллельны. По характеру расположения зубьев на зацепляющихся колесах они разделяются на прямозубые, косозубые и шевронные.
В конических передачах (рис. 5.1б) оси валов пересекаются. Наиболее распространены конические передачи с прямым углом между осями валов.
В гиперболоидных передачах (рис. 5.1.в) оси валов перекрещиваются. В свою очередь эти передачи подразделяются на гипоидные, винтовые и червячные. Последние являются частным случаем винтовых передач и состоят из червяка и червячного колеса.
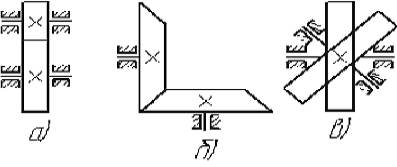
Рис. 5.1. Кинематические схемы цилиндрической (а), конической (б) и гиперболоидной (в) зубчатых передач.
Преимуществами зубчатых передач перед другими (фрикционными, ременными, цепными) являются постоянство передаточного отношения, высокий механический КПД, долговечность и компактность.
Недостатком является то, что наличие высшей кинематической пары в месте контакта зубьев приводит к большим контактным напряжениям. Тем самым при их эксплуатации приходится ограничивать величину передаваемых усилий, упрочнять поверхности зубьев в зоне их контакта, применять систему смазки колес.
5.2. Передаточное отношение
Передаточное отношение – это отношение угловых скоростей взаимодействующих (зацепляющихся) зубчатых колес. Если взаимодействие колес внешнее, то их передаточное отношение отрицательно (рис.5.2) (U1-2 < 0), если взаимодействие внутреннее, то U1-2 > 0 (рис.5.3). Знак «+» указывает на совпадение векторов угловых скоростей (направлений вращения колес).
Численно величина передаточного отношения ступени равна отношению угловых скоростей 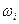 , (1/с), частот вращений
, (1/с), частот вращений 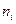 , (об/мин) или обратному отношению количества зубьев колес
, (об/мин) или обратному отношению количества зубьев колес 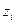 :
:
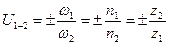
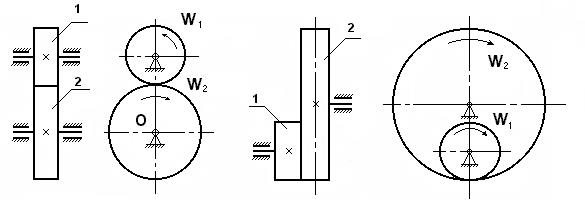
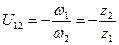
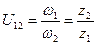
| Рис. 5.2. Пара зубчатых колес с внешним зацеплением | Рис. 5.3. Пара зубчатых колес с внутренним зацеплением |
Передаточное отношение сложных (многоступенчатых) зубчатых передач (рис. 5.4) равно произведению передаточных отношений ступеней:
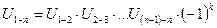 ,
,
где 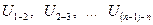 – передаточные отношения ступеней;
– передаточные отношения ступеней;
k – количество ступеней.
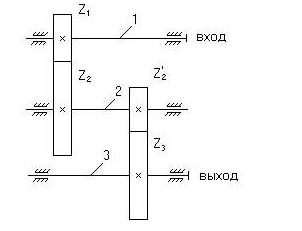
Рис. 5.4. Двухступенчатая зубчатая передача
Например, для двухступенчатой зубчатой передачи, кинематическая схема которой представлена на рис. 5.4, величину передаточного отношения можно вычислить так:
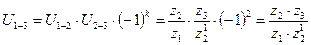
5.3 Основные геометрические параметры зубчатого колеса цилиндрической передачи
Рассмотрим геометрические параметры зубчатого колеса цилиндрической передачи в плоскости, перпендикулярной оси его вращения (рис. 5.5).
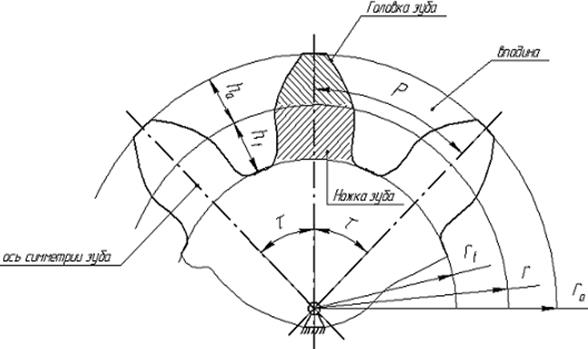
Рис. 5.5 Геометрические параметры зубчатого колеса
Каждый зуб колеса имеет ось симметрии, проходящую через ось вращения колеса О. Угол между осями симметрии называется угловым шагом τ. Число зубьев колеса z=2π/τ (если τ измеряется в радианах) или z=360º / τ (если τ – в угловых градусах). Внешняя граница зуба очерчивается окружностью выступов радиусом ra, а внутренняя часть впадины – окружностью впадин радиусом rf.
Окружность радиусом r делит зуб по высоте на головку и ножку. Расстояние между одноименными профилями соседних зубьев по дуге этой окружности (или между соседними осями симметрии зубьев) называется окружным шагом P.
Длину окружности диаметром d=2r можно выразить так:
L=P×z= π×d,
откуда d=(P/π) ×z.
Величину P/π = m называют модулем. На него введен ГОСТ 9563-60, в соответствии с которым при расчетах геометрических параметров зубчатых колес его выбирают из стандартного ряда в пределах m = 0,05…100 мм.
Окружность, по которой модуль m является стандартной величиной, называется делительной окружностью с диаметром d = m×z или радиусом r = (m×z)/2.
Все остальные геометрические параметры зубчатого колеса в соответствии с ГОСТом пропорциональны модулю m:
- высота головки зуба ha = m,
- высота ножки зуба hf = 1,25m,
- высота зуба h = ha+hf = 2,25m,
- радиус окружности выступов
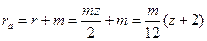
- радиус окружности впадин
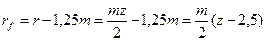
- окружной шаг P=π×m,
- толщина зуба по делительной окружности
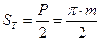
-ширина впадин по делительной окружности
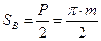
Ширину колеса “ в ” принимаем в пределах в = (10…30)m.
Межосевое расстояние двух зацепляющихся колес нулевого зацепления
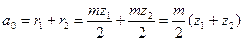 ,
,
где r1 и r2 – радиусы делительных окружностей зацепляющих колес,
z1 и z2 – их число зубьев.
В зацепление друг с другом могут входить только зубчатые колеса, имеющие одинаковый модуль m и окружной шаг P.
5.4 Основная теорема зацепления
Вывод теоремы и ее формулировка определяют условие, которому должны отвечать боковые профили зубьев, находящихся в зацеплении друг с другом.
Рассмотрим картину касания двух боковых профилей зубьев. Пусть эти профили будут очерчены какими-то кривыми (рис. 5.6), касающимися друг друга в точке М.
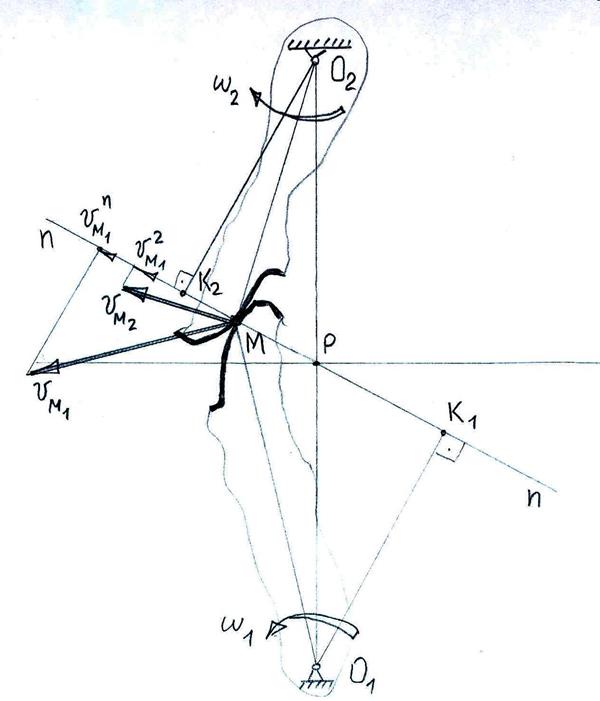
Рис. 5.6 Картина зацепления двух соприкасающихся боковых профилей.
Прямая n-n является общей нормалью к этим кривым. Представим вращение профилей зубьев вокруг осей О1 и О2 с угловыми скоростями ω1 и ω2. Тогда векторы окружных скоростей 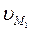 и
и 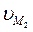 точек M1 и M2, принадлежащих этим профилям, будут направлены перпендикулярно радиусам О1M и O2M, а их величины будут равны:
точек M1 и M2, принадлежащих этим профилям, будут направлены перпендикулярно радиусам О1M и O2M, а их величины будут равны:
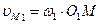 ,
,
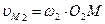 .
.
Спроектируем эти скорости на нормаль n-n и получим векторы 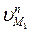 и
и 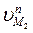
Очевидно, что для соблюдения нормальной работы зацепления необходимо обеспечить равенство этих векторов:
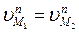
В противном случае будет или «убегание» левого профиля (если 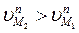 ) или «набегание» правого на левый (
) или «набегание» правого на левый (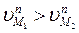 ), что в принципе невозможно.
), что в принципе невозможно.
Рассмотрим подобие треугольников:
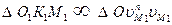 .
.
Из свойства соотношения сторон составим уравнение пропорции 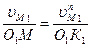 ,
,
откуда
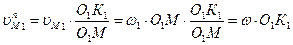 .
.
Из аналогичного подобия 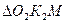 и
и 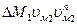 получим
получим
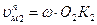
Так как 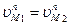 , то
, то 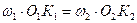
или 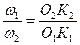 . (5.1)
. (5.1)
|
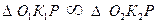 , тогда
, тогда 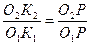 , а уравнение (5.1) запишем в виде:
, а уравнение (5.1) запишем в виде:
Это есть запись основной теоремы зацепления, которая гласит:
нормаль n-n к профилям, образующим высшую кинематическую пару, проведенная к точке их касания, делит межосевые расстояния 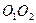 на отрезки, обратно пропорциональные угловым скоростям, с которыми эти профили вращаются.
на отрезки, обратно пропорциональные угловым скоростям, с которыми эти профили вращаются.
5.5 Эвольвента и ее свойства
Наибольшее распространение получили зубчатые колеса, у которых боковые профили зубьев очерчены кривой под названием эвольвента. Соответственно профиль такого зуба и само зацепление называется эвольвентным.
Эвольвента – кривая, которую очерчивает точка, принадлежащая прямой, перекатывающейся по окружности без скольжения.
Координаты любой точки эвольвенты определяются углом 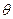 и длиной
и длиной 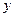 .
.
Исходя из свойств эвольвенты 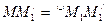 ;
; 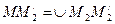 и т.д.
и т.д.
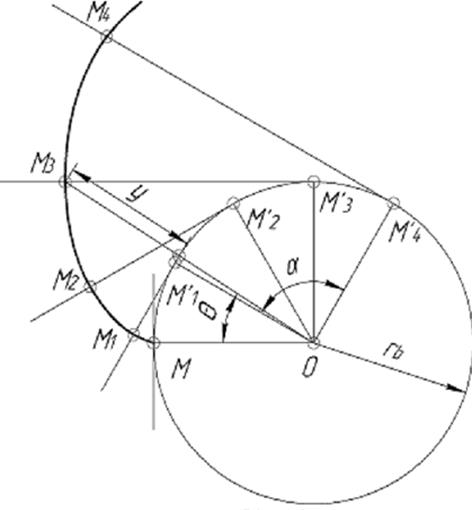
Рис. 5.7 Построение эвольвенты
Из соотношения углов и дуг окружности радиуса rb следует:
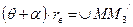 ,
,
а из треугольника ОМ3/М3 следует:
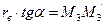 ,
,
отсюда
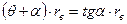 ,
,
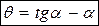 (5.2)
(5.2)
Функция угла 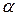 (5.2) называется инволютой угла
(5.2) называется инволютой угла 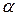 :
:
|
Для определения ее численного значения в учебниках и справочниках по расчету зубчатых передач имеются таблицы.
Координаты любой точки эвольвенты определяются углом 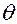 и отрезком длиной
и отрезком длиной 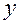 .
.
Определим зависимость 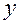 от других геометрических параметров:
от других геометрических параметров:
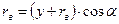 ,
,
отсюда
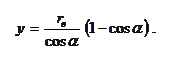
Окружность, по которой перекатывается прямая, называется основной, а ее радиус 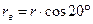 , где
, где 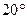 - угол наклона бокового профиля зуба инструментальной рейки, служащей для нарезания зубьев.
- угол наклона бокового профиля зуба инструментальной рейки, служащей для нарезания зубьев.
Свойства эвольвенты:
1. Все точки эвольвенты лежат вне основной окружности радиуса rb.
2. Нормаль к эвольвенте касательна к основной окружности.
3. Центры кривизны эвольвенты лежат на основной окружности.
5.6. Построение картины зацепления колес эвольвентой цилиндрической передачи.
Для построения картины зацепления необходимо знать числа зубьев колес z1 и z2, модуль m и угол зацепления 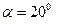 . Зацепление стандартное.
. Зацепление стандартное.
Вычисляем все необходимые геометрические параметры:
Радиусы делительных окружностей
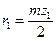 ;
; 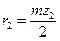 ,
,
радиусы основных окружностей
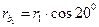 ;
; 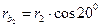 ,
,
межцентровое расстояние
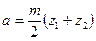 ,
,
радиусы окружностей выступов
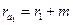 ;
; 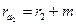 ,
,
радиусы окружностей впадин
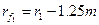 ;
; 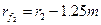 ,
,
шаг по делительной окружности 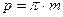 ,
,
толщину зуба и ширину впадины по делительной окружности
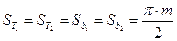 ,
,
начальные окружности 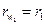 ;
; 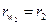 .
.
Построение картины зацепления колес
На прямой линии откладывается межосевое расстояние (рис. 5.8)
О1О2 = аW = rW1 + rW 2.
Из центров О1 и О2 проводятся дуги всех окружностей колес (делительные, основные, начальные, вершин, впадин). При этом дуги начальных окружностей должны соприкасаться в полюсе зацепления Р.
Проводится общая касательная АВ к основным окружностям. Она обязательно должна пройти через полюс зацепления Р.
Через полюс зацепления Р проводится линия, перпендикулярная отрезку О1О2.
На построенном чертеже измеряют величину угла зацепления
a W = ÐРО1А = ÐРО2В
и убеждаются в его совпадении с расчетной величиной.
С помощью шаблонов строят профили зубьев колеса 1 и колеса 2, соприкасающиеся в полюсе Р. Отмечают оси симметрии этих зубьев и, откладывая влево и вправо от них шаги (угловые ti или окружные Рi по дугам делительных окружностей), проводят оси симметрии еще двух пар зубьев, после чего по шаблонам строят их профили. При построении этих профилей следует учитывать, что они должны касаться друг друга в точках К1 и К2, которые должны лежать на нормали n1 - n1.
Определяют действительную (практическую) линию зацепления ab. Ее крайние точки лежат на пересечении теоретической линии зацепления АВ с окружностями вершин колес.
Затем находят границы рабочих участков поверхностей зубьев. Для этого радиусами О1 а и О2 b проводят дуги до пересечения их с профилями зубьев, соприкасающихся в полюсе Р.
Определяют дугу зацепления cd. Для этого один из профилей зубьев, соприкасающийся в полюсе Р с боковым профилем другого зуба, с помощью шаблона строят (пунктирной линией) в таком положении, когда он проходит через крайние точки a и b практической линии зацепления. Расстояние между этими профилями по дуге начальной окружности является дугой зацепления (È cd).
Вычисляют коэффициент перекрытия по формуле
eгрa = È cd /Р = (ab)/(cosa0.P),
где Р – окружной шаг, (ab) – длина практической линии зацепления, измеренная на чертеже – картине зацепления. Рассчитанную таким образом
величину коэффициента перекрытия сравнивают с её значением ea, найденным ранее аналитически (с использованием расчетной формулы).
Величина коэффициента перекрытия eгрa, найденная графическим методом (с использованием данных чертежа – картины зацепления колес), не должна
отличаться от её значения, 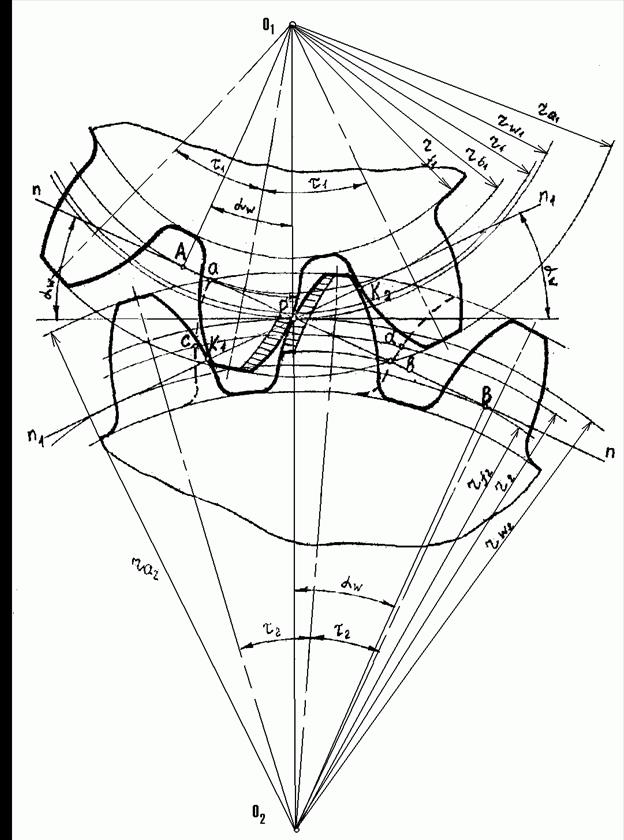
вычисленного по аналитической зависимости, более чем на 5%.
Рис.5.8. Построение картины зацепления колес
5.7. Коэффициент перекрытия
Изобразим касание боковых профилей зубьев в начале (точка a) и конце зацепления (точка b, рис. 5.9)
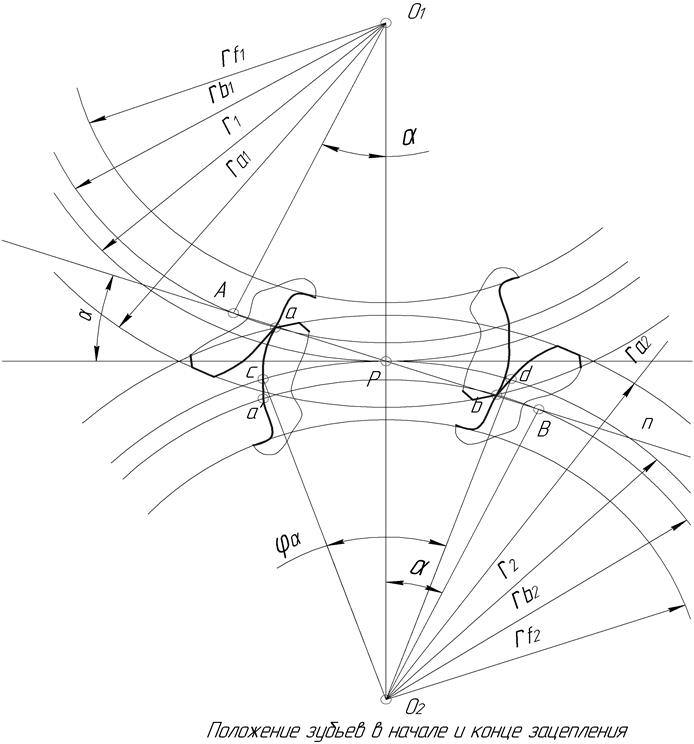
Рис. 5.9. Картина касания зубьев в начале и конце зацепления
Здесь обозначены следующие геометрические параметры:
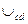 - дуга зацепления,
- дуга зацепления,
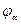 - угол зацепления,
- угол зацепления,
AB – теоретическая линия зацепления,
ab – практическая линия зацепления.
Условием непрерывности зацепления является 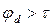 , где
, где 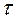 - угловой шаг. Отношение
- угловой шаг. Отношение
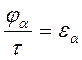 (5.3)
(5.3)
называется коэффициентом перекрытия.
Физический смысл 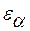 заключается в том, что он указывает, сколько пар зубьев одновременно находится в зацеплении (если
заключается в том, что он указывает, сколько пар зубьев одновременно находится в зацеплении (если 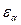 =1, то 1 пара зубьев, если
=1, то 1 пара зубьев, если 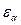 =2 – 2 пары, а если
=2 – 2 пары, а если 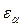 =1,5, то 50% времени в зацеплении находится 1 пара зубьев, 50% времени – 2 пары).
=1,5, то 50% времени в зацеплении находится 1 пара зубьев, 50% времени – 2 пары).
Вывод формулы расчета 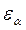 :
:
Угол зацепления 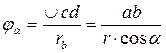 .
.
Здесь 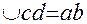 по свойству эквиваленты.
по свойству эквиваленты.
Угловой шаг 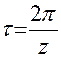 . Тогда (5.3) запишется в виде
. Тогда (5.3) запишется в виде
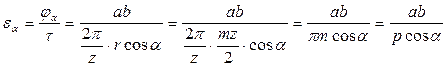 ;
;
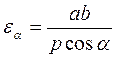 .
.
Величину ab можно взять с чертежа или вычислить аналитически. Для вывода формулы расчета ab произведем следующие преобразования. Из рис.5.9 следует, что:
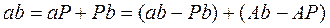 ,
,
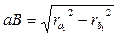 ;
; 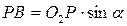 ,
,
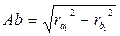 ;
; 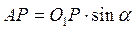 ,
,
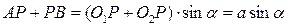 ,
,
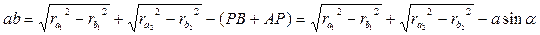 .
.
Тогда 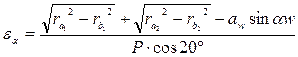 .
.
В прямозубых зацеплениях 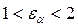 . Для увеличения коэффициента зацепления
. Для увеличения коэффициента зацепления 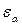 используют косозубые колеса.
используют косозубые колеса.
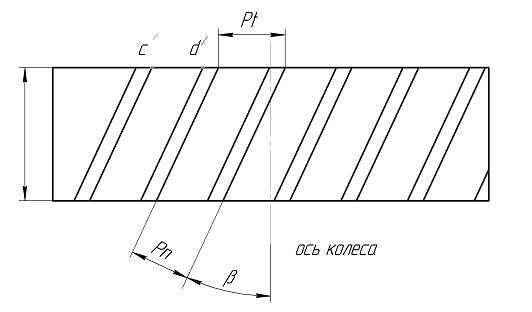
Рис 5.10. Развертка венца косозубого колеса.
На развертке венца косозубого зубчатого колеса указаны следующие размеры:
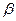 - угол наклона зубьев,
- угол наклона зубьев,
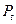 - торцевой шаг,
- торцевой шаг,
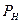 - нормальный шаг,
- нормальный шаг,
В - ширина колеса.
Длина дуги зацепления в косозубом зацеплении по сравнению с прямозубым увеличена на длину 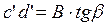 .
.
Тогда величина коэффициента перекрытия равна
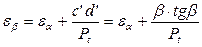 .
.
При этом
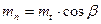 - нормальный модуль;
- нормальный модуль;
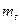 - торцевой модуль.
- торцевой модуль.
Преимущества косозубых колес: возможность передачи больших крутящих моментов при тех же габаритах, повышенная надежность, бесшумность.
Недостатки: сложность изготовления, появление осевого усилия, что требует усложнения конструкции подшипникового узла.
Для снятия осевого усилия используют шевронные колеса, представляющие собой два косозубых колеса с противоположными углами наклона зубьев. Но такие колеса более сложны в изготовлении.
5.8. Способы нарезания зубчатых колес
Зубчатые колеса с эвольвентным профилем зубьев обычно нарезают на специальных зуборезных станках двумя способами: огибанием (обкаткой) и копированием.
Огибание (обкатка)
Инструментом являются инструментальна рейка, червячная фреза или долбяк. Способ производителен и непрерывен. Его отличают простота оснастки режущего инструмента (рейки). Он широко используется в серийном и массовом производстве.
Метод обкатки заключается в том, что режущему инструменту (рейке или долбяку) и заготовке сообщают относительное движение, которое как бы имели бы два зубчатых колеса, находящиеся в правильном зацеплении. В таком случае режущий инструмент должен представлять собой зубчатое колесо с режущими гранями на зубьях долбяка (рис.2а) или зубчатую рейку (рис.2б). Инструмент – долбяк может нарезать колеса заданного модуля с числом зубьев zk ≥ zu+15, где zu – число зубьев долбяка. При этом необходимо, чтобы заготовка и долбяк вращались с соответствующими угловыми скоростями, а долбяк еще и совершал поступательное (режущее) движение вдоль оси заготовки. Этот способ позволяет нарезать методом обкатки колеса как с наружным, так и с внутренним расположением зубьев.
Вместо долбяка в качестве инструмента можно использовать инструментальную рейку (рис.2б). Рейка совершает в вертикальном направлении (в данном изображении – перпендикулярно плоскости чертежа) возвратно-поступательное движение, параллельное оси нарезаемого колеса. Заготовка имеет двойное движение в горизонтальной плоскости: вращаясь вокруг своей оси, она одновременно перемещается вдоль рейки.
. 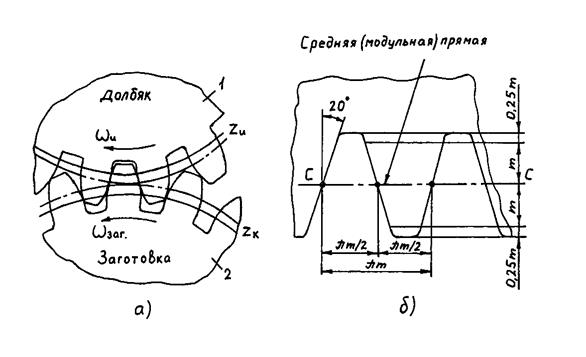
Рис.2. Долбяк (а) и инструментальная рейка (б)
Копирование
Режущим инструментом при копировании является дисковая или пальцевая фреза, режущие кромки которых имеют профиль (форму) впадины нарезаемого зубчатого колеса. За один проход инструмента нарезается одна впадина. Для вырезания следующей впадины заготовку поворачивают на величину углового шага. Этот способ распространен в мелкосерийном, единичном и ремонтном производстве, а также при изготовлении крупных колес. Способ малопроизводителен и, кроме того, требует большого количества зуборезного инструмента.
5.9. Явление подрезания зубьев.
Минимальное число зубьев колеса.
Если произойдет наложение боковых профилей зуба инструментальной рейки и зуба колеса (произойдет интерференция), то часть ножки зуба будет подрезана головкой зуба инструментальной рейки. (рис. 5.12). Часть рабочего участка зуба при этом не будет являться эвольвентой, и основная теорема зацепления не будет соблюдена, а основание зуба - ослаблено.
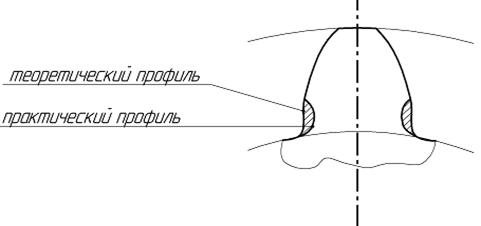
Рис.5.12. Подрезание ножки зуба
В этом случае практическая линия зацепления ab будет выходить за пределы теоретической линии AB. (рис. 5.9). Для устранения подрезания необходимо совместить точки a и A на линии зацепления. С этой целью производят так называемую коррекцию, при которой зуборезная рейка отодвигается от заготовки нарезаемого колеса на определенное расстояние, достаточное для того чтобы не происходило подрезание ножки зуба.
Рис. 5.13. Смещение инструментальной рейки при нарезании положительного колеса
Определим величину смещения рейки, необходимую для устранения подрезания ножки зуба. Для этого необходимо совместить точки A и a – точки теоретической и практической линий зацепления. При этом
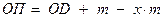 ,
,
где 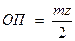 ;
; 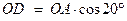 ;
; 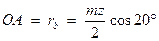 ,
,
xm – абсолютный сдвиг рейки, x – относительное смещение рейки.
Тогда 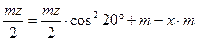 ;
;
Отсюда 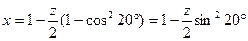 ,
,
или в общем виде (если 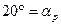 ):
):
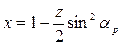 .
.
Для условия x = 0 определим минимальное число зубьев нулевого колеса, при котором не будет подрезания: 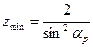 .
.
Если 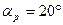 , то
, то 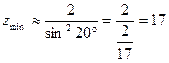 .
.
Используя это условие, можно записать для случая 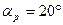 :
:
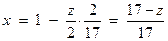 - величина относительного смещения.
- величина относительного смещения.
Если x = 0, то будет нарезано нулевое колесо, если x>0, то положительное колесо (рейка отодвинута от колеса), если x<0, то отрицательное колесо (при этом рейка будет придвинута к колесу)
5.10. Геометрические параметры коррегированных зубчатых колес
Толщина зуба по делительной окружности.
Пусть рейка придвинута к нарезаемому колесу на величину смещения инструментальной рейки x . m. Тогда толщина зуба нарезаемого колеса по делительной окружности уменьшится на 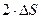 (рис.5.13).
(рис.5.13).
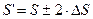 ,
,
где 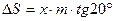 .
.
Отсюда толщина зуба колеса равна
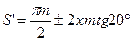 .
.
Знак «+» принимает при положительном сдвиге, когда рейка отодвинута от нарезаемого колеса, знак «-» - при отрицательном сдвиге, когда рейка придвинута к колесу.
| 
|
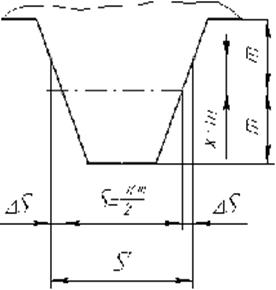
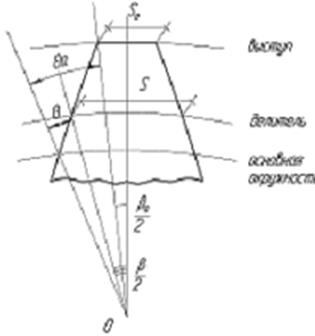
| Рис.5.14. Профиль зуба рейки | Рис.5.14 Профиль зуба колеса |
Толщина зуба по окружности выступов
Из рис.5.14 очевидно следующее равенство:
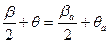 , (5.4)
, (5.4)
где 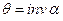 ;
; 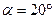 .
.
Согласно уравнению эвольвенты 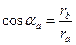 .
.
Тогда
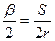 ;
; 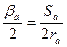 .
.
Подставив эти значения в уравнение (5.4), получим
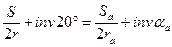 .
.
Отсюда получаем формулу расчета толщины зуба по окружности выступов:
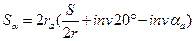 . (5.5)
. (5.5)
Допускается 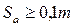 . Если это неравенство не выполняется (произошло заострение вершины зуба), проводят корректировку расчетов, уменьшая сдвиг рейки или увеличивая модуль m.
. Если это неравенство не выполняется (произошло заострение вершины зуба), проводят корректировку расчетов, уменьшая сдвиг рейки или увеличивая модуль m.
Определение угла коррегированного зацепления 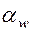
Пользуясь формулой (5.5), можно записать формулу расчета толщины зуба по начальной окружности:
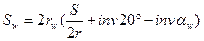
Так как 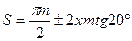 ,
, 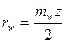 ,
, 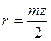 ,
,
то 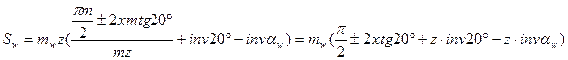 .
.
При беззазорном зацеплении сумма толщин зубьев по начальным окружностям отвечает условию 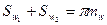 , или
, или 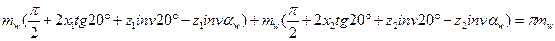
Отсюда
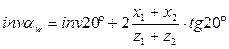 .
.
Радиусы начальных окружностей вычисляются по формуле
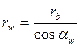 .
.
Межосевое расстояние коррегированного зацепления
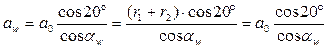 ,
,
где 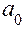 - стандартное межосевое расстояние.
- стандартное межосевое расстояние.
Тогда 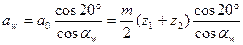 .
.
Если 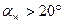 , то
, то 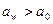 ; если же
; если же 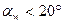 , то
, то 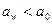 .
.
Если 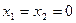 , то получаем стандартную передачу, если
, то получаем стандартную передачу, если 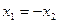 - равносмещенную передачу.
- равносмещенную передачу.
Радиусы окружностей впадин и выступов
Радиус окружности впадин вычисляется по формуле
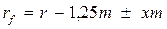 .
.
Здесь принимают знак «+» при положительном сдвиге, «-» - при отрицательном сдвиге.
Радиус окружности выступов равна
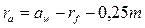 .
.
Коррегированные зацепления применяют в следующих случаях:
- если число зубьев нарезанного колеса z<17 и происходит подрезание зуба,
- если задано межосевое расстояние 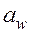 , отличное от стандартного
, отличное от стандартного 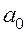 ;
;
- для улучшения качественных показателей зацепления (устранение заострения вершин зуба, уменьшение износа и т.д.).
Для выбора величины коэффициентов смещения  и
и 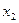 удобно использовать блокирующие контуры (рис. 5.16). Они представляют собой допустимые области значений
удобно использовать блокирующие контуры (рис. 5.16). Они представляют собой допустимые области значений 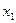 и
и 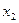 , изображенные в координатных осях
, изображенные в координатных осях  и
и 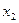 .
.
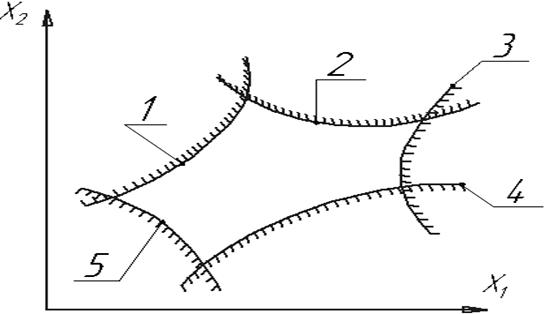
Рис.5.16. Примерная схема блокирующего контура
Кривые 1 … 5 представляют собой ограничения на заострение головок зубьев, подрезание ножек зубьев, заданные значения коэффициента перекрытия, скоростей относительного скольжения соприкасающихся профилей и т.д.
СЛОЖНЫЕ ЗУБЧАТЫЕ МЕХАНИЗМЫ
6.1. Общие сведения о сложных зубчатых механизмах
Различают одноступенчатые и многоступенчатые зубчатые механизмы.
Одноступенчатым называют такой зубчатый механизм, который не может быть расчленен на более простые.
Передаточное отношение одноступенчатого механизма целесообразно принимать не более 6...8. Иначе возрастают габариты колеса и всего механизма, происходит неравномерный износ колеса (шестерня изнашивается быстрее).
Многоступенчатые (сложные) зубчатые механизмы используют для получения больших передаточных отношений. Они образуются путем соединения нескольких одноступенчатых механизмов. Механизмы, понижающие угловую скорость, называются редукторами, повышающие – мультипликаторами.
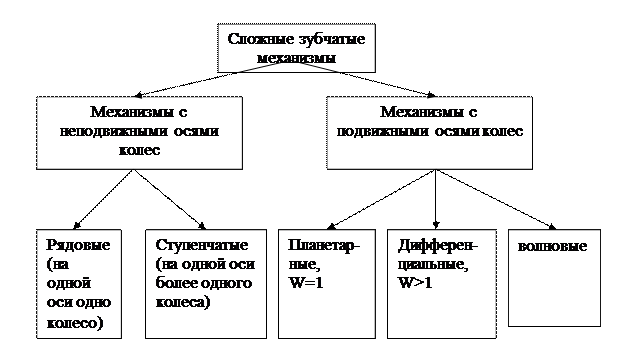
Классификация сложных зубчатых механизмов
Все сложные зубчатые механизмы можно классифицировать по характеру движения и подвижности осей валов, а также по величине передаточного отношения.
а) классификация по характеру движения (подвижности) осей валов:
б) классификация по величине передаточного отношения U:
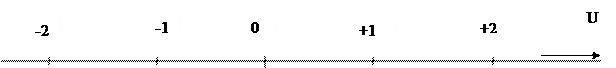 | ||||||||
 | ||||||||
| ||||||||
| ||||||||
| ||||||||
6.2. Передачи с неподвижными осями колес
Рядовой зубчатый механизм – это последовательно соединенные несколько ступеней зубчатых колес. (рис. 6.1.).
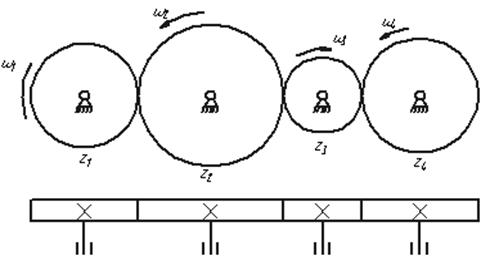
Рис.6.1. Рядовой зубчатый механизм
Согласно определению, передаточное отношение равно отношению угловых скоростей входного и выходного валов 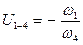 , а передаточные отношения ступеней
, а передаточные отношения ступеней 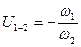 ;
; 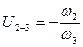 ;
; 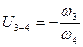 .
.
Перемножим левые и правые части этих выражений и приравняем их друг к другу:
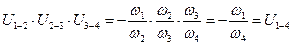 .
.
Отсюда можно записать обобщенную формулу вычисления передаточного отношения
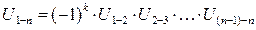 (6.1),
(6.1),
где n – количество валов, k – количество ступеней.
Так как 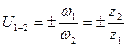 , то формула расчета общего передаточного отношения рядового механизма выглядит так:
, то формула расчета общего передаточного отношения рядового механизма выглядит так: 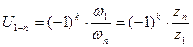 .
.
Отсюда следует, что его величина зависит только от количества зубьев входного и выходного колес. Промежуточные колеса служат лишь для увеличения межосевого расстояния и изменения направления вращения.
Ступенчатый механизм
Передаточное отношение ступенчатого зубчатого механизма рассчитывается по формуле (6.1).
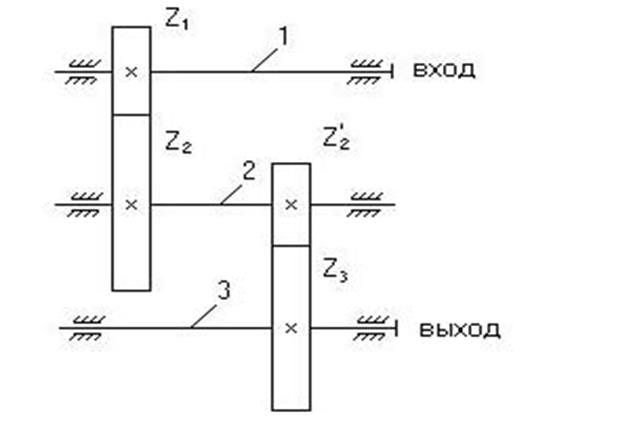
Рис. 6.2. Ступенчатый зубчатый механизм
Для механизма, изображенного на рис. 6.2, формула расчета передаточного отношения выглядит так:
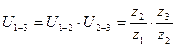 .
.
Ступенчатые механизмы применяются для:
- того же, что и рядовые, т.е. для изменения направления вращения выходного вала по отношению ко входному,
- получения больших передаточных отношений.
Например, с помощью 2х-ступенчатого механизма можно получить 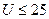 , 3х-ступенчатого -
, 3х-ступенчатого - 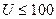 , 4х-ступенчатого -
, 4х-ступенчатого - 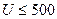 .
.
6.3. Планетарные передачи.
Различают 4 основных типа планетарных ступеней (так называемых механизмов Давида) (рис.6.3, схемы І - ІV):
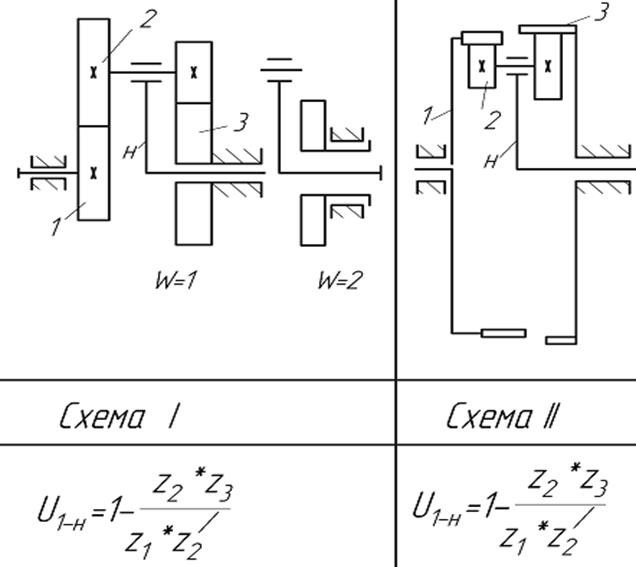
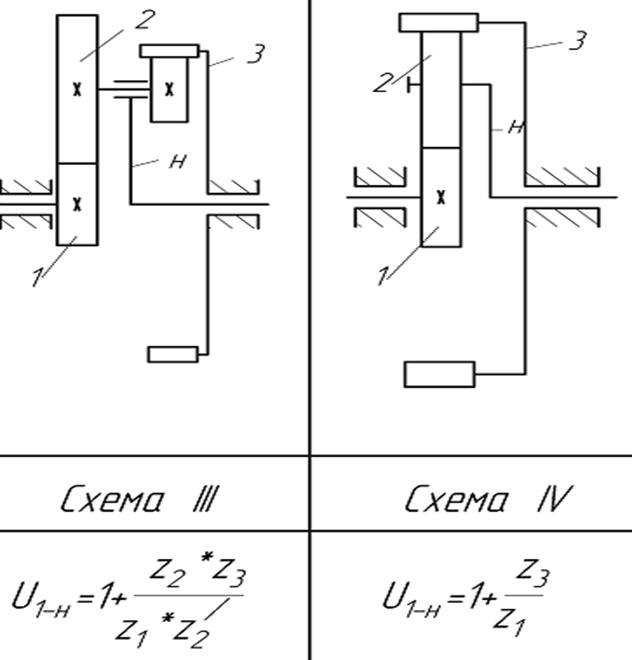
Рис.6.3. Кинематические схемы планетарных передач
Условные обозначения звеньев планетарных механизмов на рис. 6.3: 1 – центральное колесо, 2 – сателлиты, 3 – опорное (неподвижное) колесо; H – водило (от заглавной буквы слова Hedel – рычаг).
Преимущества планетарных передач:
- компактность при больших передаточных отношениях U;
- возможность передачи больших крутящих моментов (т.к. при их передаче используется несколько сателлитов);
Недостатки планетарных передач:
- сложность изготовления;
- требуются высокая точность изготовления и сборки.
6.3.1. Вычисление передаточного отношения планетарной передачи
Аналитический метод. Используем метод обращения движения – т.е. всему механизму, в том числе неподвижному колесу, условно придается (сообщается) угловая скорость - 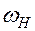 (то есть все звенья в таком механизме уменьшают скорость на величину угловой скорости водила
(то есть все звенья в таком механизме уменьшают скорость на величину угловой скорости водила 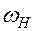 ). Тогда в этом так называемом обращенном механизме водило H станет неподвижным, и мы получим простой ступенчатый механизм с неподвижными осями. Угловые скорости исходного планетарного и обращенного механизма сведем в таблицу:
). Тогда в этом так называемом обращенном механизме водило H станет неподвижным, и мы получим простой ступенчатый механизм с неподвижными осями. Угловые скорости исходного планетарного и обращенного механизма сведем в таблицу:
| №№ звеньев | Угловые скорости | |
| В планетарном механизме | В обращенном механизме | |
| H | 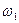
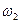
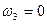
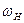
| 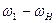
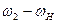
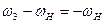
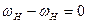
|
Вычисляем передаточные отношения обращенного механизма (на примере схемы I):
через угловые скорости