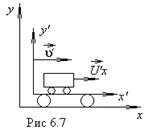
Рис.6.7. Рассмотрим движение материальной точки
В системе X
- положение точки определяется в каждый момент времени t координатами x,y,z.
- Выражения
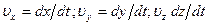представляют собой проекции вектора скорости точки на соответствующие оси в системе отсчета X.
В системе 
- положение материальной точки характеризуется в каждый момент времени
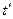координатами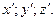 
- Проекции вектора скорости относительно на эти оси определяются выражениями
.
Из формул (6.2) получаем
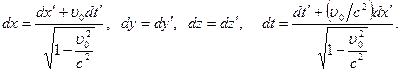
Разделив первые три равенства на четвертое, получаем формулы для преобразования скоростей при переходе их одной системы отсчета в другую:
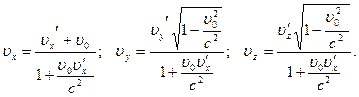(6.3)
При 
эти соотношения переходят в преобразования Галилея в классической механике.
Обратные преобразования имеют вид:
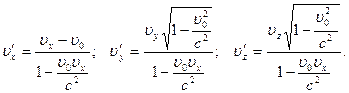
Если тело движется параллельно оси x,
· его скорость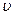 
относительно системы X совпадает с 
,
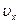· а скорость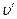 
относительно системы - с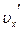 
.
В этом случае закон сложения скоростей принимает вид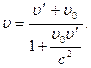 
(6.4)
Если скорость частицы в одной системе отсчета 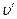= c, то в другой системе, согласно (6.4) эта скорость равна
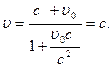
Мы получили, что скорость света одинакова во всех инерциальных системах отсчета.
Преобразования для импульса и энергии
Уравнения Ньютона
· инвариантны по отношению к преобразованиям Галилея.
· неинвариантными к преобразованиям Лоренца.. В частности, не инвариантен к преобразованиям Лоренца вытекающий из законов Ньютона закон сохранения импульса.
Импульс - в теории относительности, как и в Ньютоновской механике, равен произведению массы тела на его скорость
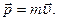(6.5)
Масса. О днако в выражении (6.5) масса не является постоянной величиной, а зависит от скорости по закону
. (6.6)
Величина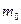 
называется массой покоя - это инвариантная величина, масса 
носит название релятивистской массы.
Рис.6.8. Зависимость релятивистской массы от скорости.
Продифференцировав выражение (6.5) по времени, получаем
релятивистское выражение второго закона Ньютона 
Чтобы найти релятивистское выражение для энергии, умножим это уравнение на перемещение частицы 
:
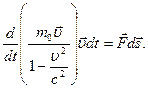
Правая часть этого выражения равна работе, совершаемой над частицей за время dt.
Как следует из закона сохранения энергии, эта работа равна приращению энергии частицы:
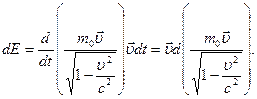
Преобразуем полученное выражение:
Проинтегрировав, имеем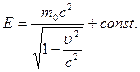 
Экспериментально доказано, что константа в этом выражении равна нулю.
Тогда полная энергия частицы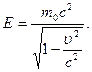 
(6.7)
Если скорость частицы равна нулю, энергия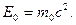 
- это энергия покоя.
· Она не связана ни с каким движением частицы.
· Для произвольного тела энергия покоя равна сумме энергий покоя всех его частиц, кинетических энергий этих частиц в системе центра масс тела и потенциальных энергий взаимодействия этих частиц.
· В энергию покоя, как и в полную энергию, не входит потенциальная энергия тела в поле внешних сил.
Кинетическая энергия равна разности между полной энергией и энергией покоя частицы:
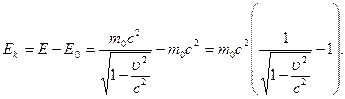
В случае малых скоростей 
эта формула преобразовывается к виду:
Мы получили классическое выражение для кинетической энергии частицы.
Решив совместно уравнения (6.5), (6.6) и (6.7), получаем: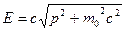 
. (6.8)
При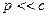 
имеем: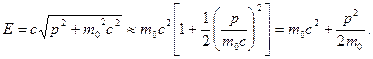 
Это выражение отличается от классического выражения для кинетической энергии слагаемым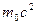 
.
Из выражения (6.7) следует еще одна формула для энергии: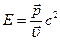 
.
Тогда импульс частицы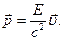 
Получим еще одну формулу для энергии.
Из замедления времени получаем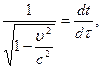 
где 
- промежуток времени между двумя происходящими с частицей событиями, отсчитанный по часам в той системе отсчета, в которой частица движется,
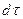- тот же промежуток времени, отсчитанный по часам, движущимся вместе с частицей.
Подставив это выражение в формулу (6.7), имеем 
(6.9)
Получим теперь преобразования импульса и энергии.
Из (6.8) следует 
(6.10)
Масса 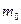является инвариантом, следовательно, и выражение (6.10) представляет собой инвариант, т.е. имеет одинаковую величину во всех инерциальных системах отсчета. Сами по себе величины E и 
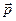не являются инвариантами, так как они зависят от скорости, которая меняется при переходе из одной системы отсчета в другую.
1. Будем считать, что частица движется параллельно оси x,
· в системе скорость частицы равна 
.
· Тогда согласно релятивистской теореме сложения скоростей скорость в системе X равна
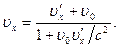6.11)
Здесь 
- скорость, с которой система движется относительно системы X.
Энергию в системе X выразим через .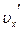
Для этого вычислим выражение 
:
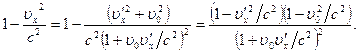
Тогда энергия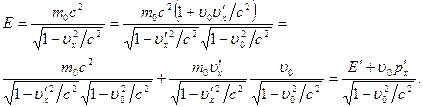 
Полученная формула справедлива при любой взаимной ориентации векторов 
и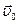 
. Это означает, что в преобразованиях участвует только компонента импульса 
.
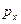Так как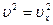 
,
выражение для импульса принимает вид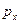 
= 
.
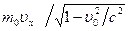Подставим в него 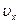из (6.11), имеем
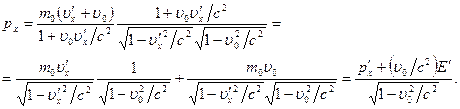
2. будем считать, что
· в системе частица движется параллельно оси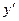 
и, следовательно, 
.
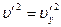· В системе Xкомпонента скорости частицы по оси x равна ,
так что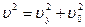 
.
Соответственно,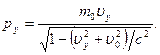 
Так как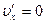 
, то из преобразований Лоренца для скоростей 
, и
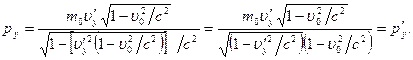
Аналогичный результат получается для компоненты 
.
Тогда преобразования для энергии и импульса принимают вид:
Эти формулы совпадают с формулами (6.2) преобразования координат и времени.
По аналогии с трехмерными векторами в евклидовом пространстве можно определить четырехмерные векторы.
Под четырехмерным вектором понимают совокупность четырех величин 
преобразующихся по тем же формулам, что и ct, x,y, z.
Квадрат такого вектора равен 
.
Вследствие того, что компоненты преобразуются так же, как координаты, квадрат четырехмерного вектора оказывается инвариантным по отношению к преобразованиям Лоренца.
Тогда совокупность величин 
образует четырехмерный вектор, называемый вектором энергии-импульса. Квадрат этого вектора является инвариантом и равен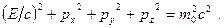 
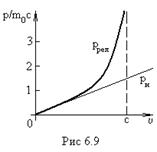
рис.6.9. Зависимость релятивистского импульса от скорости.
При малых скоростях релятивистский импульс совпадает с классическим.