Лекции 33,34. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд (4ч)
Содержание лекции:
Ряды Тейлора и Маклорена. Разложение функции в степенной ряд, необходимое, достаточные условия. Приложения степенных рядов. Примеры.
Разложение в ряд Маклорена некоторых элементарных функций. Приближенное вычисление значений функции с помощью степенных рядов.
Ряд Тейлора и Маклорена
Пусть дана функция f (x), непрерывная на некотором множестве D и х 0Î D. Если $ сходящийся степенной ряд  такой, что сумма этого ряда совпадает с f (x) в некоторой окрестности точки х 0,, т.е.
такой, что сумма этого ряда совпадает с f (x) в некоторой окрестности точки х 0,, т.е.
 = f (x),
= f (x),
то говорят, что функция f (x) разлагается в степенной ряд в окрестности точке х 0 (или в ряд по степеням х – х 0).
Теорема 2.
Если функция f (x) разлагается в ряд по степеням (х – х 0), то коэффициенты этого ряда равны  .
.
Доказательство. Пусть в окрестности х 0 справедливо разложение
f (x) = а 0 + а 1(х – х 0) + а 2(х – х 0)2 + а 3(х – х 0)3 + а 4(х – х 0)4 +... (3)
Положим в этом равенстве х = х 0, получим а 0 = f (x 0).
Так как ряд в окрестности х 0 сходится, то его можно дифференцировать. Продифференцируем равенство (3) п раз, получим
f¢ (x) = а 1 +2 а 2(х – х 0) + 3 а 3(х – х 0)2 + 4 а 4(х – х 0)3 +...,
f¢¢ (x) = 2 а 2+ 6 а 3(х – х 0) +12 а 4(х – х 0)2 +...,
f¢¢¢ (x) = 6 а 3+ 24 а 4(х – х 0) +...,
..........................
f (п) (x) = п (п –1)(п –2)...2 ап + (п +1) п (п– 1)...2 ап +1(х – х 0) +...
Полагая в этих равенствах х = х 0, получим
f¢ (x 0) = а 1, или а 1= f¢ (x 0),
f¢¢ (x 0) = 2 а 2, откуда  ,
,
f¢¢¢ (x 0) = 6 а 3, откуда  ,
,
.............
f (п) (x 0) = п (п –1)(п –2)...2 ап, откуда 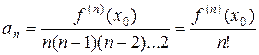 . ЧТД.
. ЧТД.
Определение 1. Степенной ряд  называется рядом Тейлора в точке х 0 для функции f (x), а коэффициенты этого ряда называются коэффициентами Тейлора для функции f (x).
называется рядом Тейлора в точке х 0 для функции f (x), а коэффициенты этого ряда называются коэффициентами Тейлора для функции f (x).
Из теоремы 7.2. следует:
1) если функция f (x) разлагается в степенной ряд в окрестности точки х 0, то это есть обязательно ряд Тейлора этой функции:
f (x) =  .
.
2) Если функция f (x) разложима в степенной ряд в окрестности точки х 0, то она бесконечное число раз дифференцируема в этой окрестности (это свойство называют необходимым условием разложимости в степенной ряд).
Теорема 7.2. формулирует необходимое, но не достаточное условие разложимости функции в степенной ряд. Т.е. нельзя утверждать, что ряд Тейлора, формально составленный для функции f (x), сходится обязательно к этой функции.
Например, функция  бесконечно дифференцируема в окрестности нуля, но ее ряд Тейлора имеет совершенно другую сумму.
бесконечно дифференцируема в окрестности нуля, но ее ряд Тейлора имеет совершенно другую сумму.
Достаточные условия сходимости ряда Тейлора к самой функции (т.е. разложимости функции в степенной ряд) дает следующая
Теорема 3.
Для того чтобы функция f (x) могла быть разложена в степенной ряд (ряд Тейлора) в окрестности U(x 0) точки х 0, необходимо и достаточно, чтобы остаток этого ряда стремился к нулю при п ®¥ " х из этой окрестности, т.е.
f (x) =  Û
Û 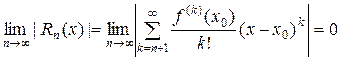
для всех х ÎU(x 0).
При этом исследование поведения остатка ряда удобно проводить, используя различные формы записи остатка ряда, в частности форму Лагранжа:
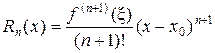 ,
,
где x – некоторое число, удовлетворяющее условию 0 < |x – x 0| < | x – x 0|, т.е. число x расположено между х и х 0.
Определение 2.
Функция, которая на некотором интервале может быть представлена своим сходящимся рядом Тейлора, называется аналитической на этом интервале.
Из определения следует, что сумма сходящегося степенного ряда есть аналитическая функция в интервале сходимости ряда.
Разложение функций в степенной ряд
Вопрос представления функции многочленом Тейлора мы рассматривали еще в первом семестре. Естественно поставить вопрос разложения функции в степенной ряд. Учитывая предыдущую информацию, можно определить следующий алгоритм разложения функции f(x) в степенной ряд в окрестности заданной точки х 0:
1. Найти производные заданной функции до п -го порядка включительно (т.е. записать формулу для f (п)(x)) и вычислить их значения в точке х 0.
2. Записать формально ряд Тейлора для f (x).
3. Найти область сходимости этого ряда.
4. Выяснить, для каких х из области сходимости ряда выполняется условие  0
0
Пример 1. Разложим функцию ех в ряд в окрестности точки х = 0 (ряд Тейлора с центром в точке х = 0 называется рядом Маклорена). Будем пользоваться сформулированным алгоритмом.
1. Очевидно, f (п)(x) = ех, тогда f (п)(0) = 1
2. ряд Тейлора имеет вид 
3. Радиус сходимости этого ряда найдем, используя формулу  . Так как
. Так как  , то
, то  , значит, ряд сходится на всей числовой прямой.
, значит, ряд сходится на всей числовой прямой.
4. Изучим поведение остатка ряда. Запишем остаток ряда в форме Лагранжа:
 à
à  , где 0 < |x| < | x |. Заметим, что здесь
, где 0 < |x| < | x |. Заметим, что здесь 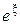 – некоторое (конечное) число, а
– некоторое (конечное) число, а  – (п +1)-й член рассмотренного ряда Тейлора, а так как ряд сходится " х, то его п -й член (а значит и п +1-й) стремится к 0 при возрастании п. Тогда
– (п +1)-й член рассмотренного ряда Тейлора, а так как ряд сходится " х, то его п -й член (а значит и п +1-й) стремится к 0 при возрастании п. Тогда
 " х.
" х.
Значит, ех =  , х Î R.
, х Î R.
Пример 2. Разложим в ряд Маклорена функцию f (x) = sin x. Имеем:
f (x) = sin x, f (0) = 0
f¢ (x) = cos x = sin  , f ¢(0) = 1
, f ¢(0) = 1
f¢¢ (x) = –sin x = sin (x + p), f ¢¢(0) = 0
f¢¢¢ (x) = –cos x = sin  , f ¢¢¢(0) = –1
, f ¢¢¢(0) = –1
f IV(x) = sin x = sin (x + 2p), f IV(0) = 0,
.....................
f (n)(x) = sin  , f (2 k)(0) = 0, f (2 k –1)(0) = (–1) k +1.
, f (2 k)(0) = 0, f (2 k –1)(0) = (–1) k +1.
Тогда ряд Тейлора имеет вид
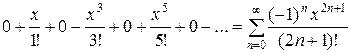
Найдем область сходимости этого ряда:
 < 1" х
< 1" х
Значит, область сходимости – вся числовая прямая.
Остаток ряда в форме Лагранжа имеет вид

Тогда | Rn (x)| = 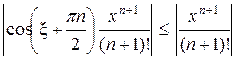 и
и
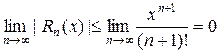 , значит
, значит 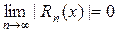 " х.
" х.
Таким образом, 
 " х Î R.
" х Î R.
Учитывая свойства степенных рядов, находим, продифференцировав полученное разложение:


То есть имеем разложение cos x =  , " х Î R.
, " х Î R.
Ранее мы получили разложения
 , | x |< 1, и
, | x |< 1, и  , х Î(-1; 1].
, х Î(-1; 1].
Если в первом из этих равенств положить х = t 2, получим
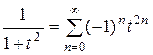 , или, в привычных символах,
, или, в привычных символах, 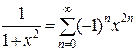 , х Î(-1; 1).
, х Î(-1; 1).
Проинтегрировав последнее равенство, получим
 , т.е.
, т.е.
 , х Î(-1; 1).
, х Î(-1; 1).
Заметим, что в граничных точках полученный ряд сходится условно:
при х = –1 имеем  , а при х = 1 получаем
, а при х = 1 получаем  ; оба эти ряда сходятся по признаку Лейбница (проверьте!). Ряд из модулей членов этих рядов один и тот же
; оба эти ряда сходятся по признаку Лейбница (проверьте!). Ряд из модулей членов этих рядов один и тот же  и он расходится, что можно без труда доказать, пользуясь интегральным признаком. Тот факт, что данные ряды сходятся соответственно к arctg(–1) =
и он расходится, что можно без труда доказать, пользуясь интегральным признаком. Тот факт, что данные ряды сходятся соответственно к arctg(–1) =  и arctg1 =
и arctg1 = 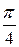 мы сможем доказать позже, изучив тригонометрические ряды. Итак,
мы сможем доказать позже, изучив тригонометрические ряды. Итак,  , х Î[-1; 1].
, х Î[-1; 1].
Пользуясь вышеописанным алгоритмом можно получить следующее разложение
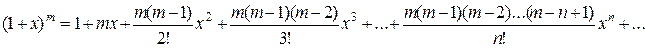 , х Î(-1,1).
, х Î(-1,1).
Таким образом, мы имеем перечень известных разложений:
I. ех =  , х Î R
, х Î R
II. 
 " х Î R
" х Î R
III. cos x =  , " х Î R.
, " х Î R.
IV.  , | x |< 1,
, | x |< 1,
V.  , | x |< 1.
, | x |< 1.
VI.  , х Î(-1; 1].
, х Î(-1; 1].
VII.  , х Î[-1; 1].
, х Î[-1; 1].
VIII.  , | x | < 1
, | x | < 1
Как следует из рассмотренных примеров, разложение в ряд заданной функции можно осуществить двумя способами: по определению (т.е. пользуясь описанным алгоритмом) и пользуясь известными разложениями, делая разного рода подстановки, дифференцируя или интегрируя ряд почленно.
Рассмотрим другие примеры разложений.
Пример 3. Разложить заданные функции по степеням х
1)  ,
,
-3 х Î(-1; 1] à  ,
,
итак  "
" 
2) 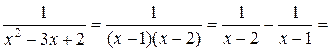

Найдем интервал сходимости полученного ряда: х Î(-1; 1) и  Î(-1; 1), откуда
Î(-1; 1), откуда 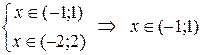 .
.
Пример 4. Разложить функцию f (x) по степеням х – х 0.
1) f (x) =  , х 0 = 4.
, х 0 = 4.
 ,
,
 .
.
Итак, 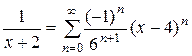 , х Î(-2;10)
, х Î(-2;10)
2) f (x) = cos2 x, х 0 = 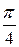 .
.

 ,
,
 .
.