1) Пусть 
только слева, оставаясь меньше x.
def. Число b1 называется пределом функции f(x) в т.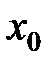 
слева (левосторонним пределом), если
.
Обозначают: 
или 
2) Пусть теперь справа, т.е. х остается больше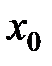 
.
def. Число b2 называется пределом функции f(x) в т. 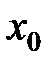справа (правосторонним п ределом), если
.
Обозначают: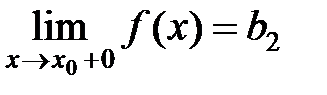 
или 
Пределы слева и справа называются односторонними пределами функции.
3) Если функция f(x) во внутренней т. 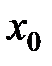имеет предел, то она имеет пределы в т. 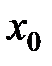слева и справа, причем
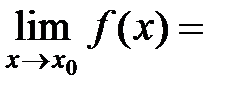
Справедливо и обратное: если односторонние пределы функции в т. 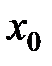существуют и равны, то будет существовать и предел функции в т. 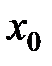, равный им.
Но односторонние пределы могут существовать, но не равняться друг другу.
| x |
| y |
| 0 |
| 1 |
| 2 |
| -1\\ |
| 1 |
| 2 |
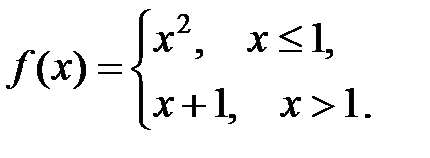
в точке x =1 функция терпит разрыв.
Замечание 1. Предел функции при 
.
| x |
| y |
| 0 |
| b |
| x |
| y |
| 0 |
| b |
Замечание 2. Бесконечный предел функции
.
(Если 
то 
если 
то 
Пример 8.2. 
IV. Распространение теорем о пределах переменнона случай функции
Все теоремы, доказанные для переменной величины, справедливы и для функций произвольной действительной переменной.
Например: 
Различные виды неопределенностей и их раскрытие
Ранее рассмотрели теоремы о пределах суммы, разности, произведения, частного, где пределы рассмотренных компонент существовали и были конечны. Рассмотрим случаи, когда пределы бесконечны или случай, когда предел делителя равен нулю.
I. Неопределенность вида 
Пусть 
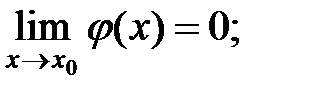
1) Пусть 
рациональная дробь (отношение двух многочленов).
Выделить множитель 
и сократить дробь на него. Такое сокращение возможно, т.к. 
но 
, т.е.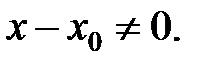 
Пример 9.1. 
2) Пусть дробь, содержащая иррациональные выражения.
«Избавиться» от иррациональности, домножив числитель и знаменатель на соответствующее сопряженное выражение.
Пример 9.2. 
3) Для раскрытия неопределенности , содержащей тригонометрические выражения, применяют 1-й замечательный предел.
II. Неопределенность вида 
Для того, чтобы раскрыть неопределенность вида , заданную отношением двух многочленов, надо числитель и знаменатель разделить на наибольшую степень переменного.
Пример 9.3. 
Пример 9.4. 
Пример 9.5. 
Замечание. 
, 
, 
III. Неопределенность вида 
Неопределенность вида преобразуется к неопределенности вида или путем умножения и деления на сопряженную величину или приведения к общему знаменателю.
Пример 9.6. 
Пример 9.7. 
IV. Неопределенность вида 
Неопределенность вида сводится к неопределенности или .
Пример 9.8.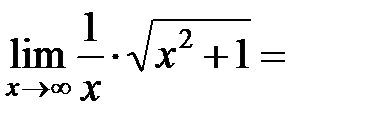 
Первый признак существования предела
def. Переменная 
(числовая последовательность 
) называется
· неубывающей, если 
· возрастающей, если 
· невозрастающей, если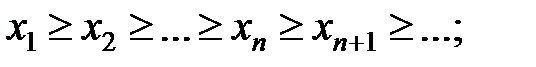 
· убывающей, если 
Возрастающие и убывающие переменные называются монотонными.
def. Переменная называется ограниченной сверху, если все ее значения не превосходят некоторого числа M, т.е. 
def. Переменная называется ограниченной снизу, если 
Теорема. Первый признак существования предела
Если переменная возрастает и ограничена сверху, то она имеет конечный предел.
Если переменная убывает и ограничена снизу, то она имеет конечный предел.