ЛИНЕЙНАЯ АЛГЕБРА
Методические указания к практическим занятиям
для студентов по направлению подготовки
38.03.01 – Экономика
Воронеж 2016
УДК 512.8
Раецкая, Е. В. Линейная алгебра [Текст]: методические указания к практическим занятиям для студентов по направлению подготовки 38.03.01 – Экономика / Е. В. Раецкая, И.В. Сапронов, Н.М. Спирина; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2016. – 32 с.
Печатается по решению учебно-методического совета
ФГБОУ ВО «ВГЛТУ» (протокол № 5 от 22 апреля 2016 г.)
Рецензент д-р физ.-мат. наук, доцента кафедры математического анализа ВГУ Зубова С.П.
Содержание
Введение……………………………………………………………………………..4
1.Матрицы и определители……………………………………………………….5
1.1 Практическая часть……………………………………………………………5
1.2 Индивидуальные задания……………………………………………………..7
2.Системы линейных уравнений……………………………………………...….9
2.1 Практическая часть……………………………………………………………9
2.2 Индивидуальные задания……………………………………………………15
3. Векторная алгебра……………………………………………………………..16
3.1 Практическая часть………………………………………………….……….16
3.2 Индивидуальные задания…………………………………………………...19
4. Аналитическая геометрия…………………………………………………….20
4.1 Практическая часть…………………………………………………………..20
4.2 Индивидуальные задания…………………………………………………...25
5. Кривые второго порядка……………………………………………………..26
5.1 Практическая часть…………………………………………………………..26
5.2 Индивидуальные задания…………………………………………………...29
Вопросы для контроля. ………………………………………………………….31
Библиографический список…………………………………………………...32
ВВЕДЕНИЕ
Целью изучения дисциплины «Линейная алгебра» является воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления, обучение основным математическим понятиям и методам линейной алгебры, необходимым для анализа и моделирования устройств, процессов и явлений при поиске оптимальных решений практических задач, методам обработки и анализа результатов численных экспериментов для экономических задач.
Основной задачей является выработка умения решать примеры и задачи для последующего применения математических методов в различных приложениях.
Студент по результатам освоения дисциплины «Линейная алгебра» должен обладать способностью выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы.
В результате освоения дисциплины студент должен:
- знать основные понятия, определения и методы исследования объектов с помощью теорем и формул различных разделов курса математики;
- уметь: решать задачи и примеры по различным разделам высшей математики с доведением решения до практического приемлемого результата (формулы, числа, графика, качественного вывода и т.п.),
- уметь при решении задач выбирать необходимые вычислительные методы и средства (ПЭВМ, таблицы и справочники);
-самостоятельно изучать научную литературу по математике;
- иметь представление о численных алгоритмах решения математических и прикладных задач его профессиональной области.
МАТРИЦЫИ ОПРЕДЕЛИТЕЛИ
ПРАКТИЧЕСКАЯ ЧАСТЬ
Матрицей А размера 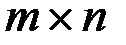 называется таблица из
называется таблица из 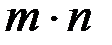 чисел
чисел
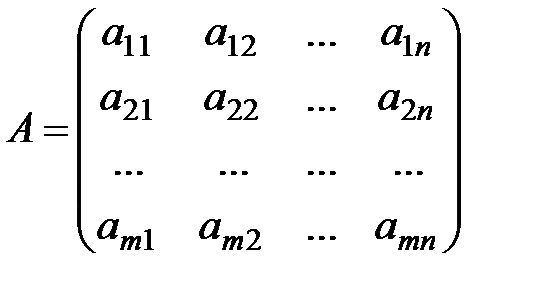
Часто для краткости пишут 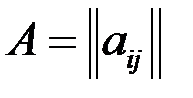 . Числа, из которых состоит матрица, называются элементами матрицы. Индексы у элементов матрицы указывают расположение этого элемента в таблице: первый индекс – номер строки, в которой находится элемент, а второй – номер столбца. Например, элемент
. Числа, из которых состоит матрица, называются элементами матрицы. Индексы у элементов матрицы указывают расположение этого элемента в таблице: первый индекс – номер строки, в которой находится элемент, а второй – номер столбца. Например, элемент 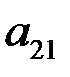 находится на пересечении второй строки и первого столбца:
находится на пересечении второй строки и первого столбца:
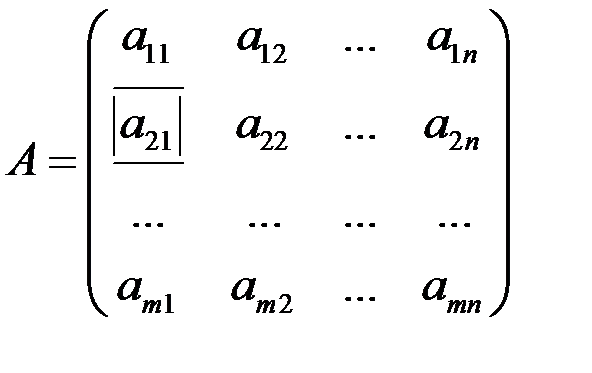
Суммой двух матриц одинакового размера 
 и
и 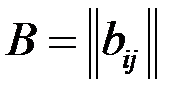 называют матрицу
называют матрицу 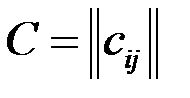 размера
размера 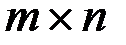 такую, что
такую, что
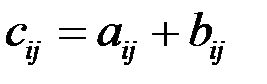 ,
, 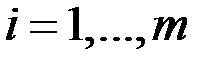 ;
; 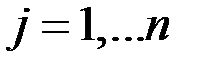 .
.
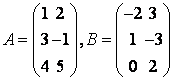
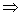
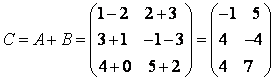 .
.
Произведением матриц АВ называется матрица
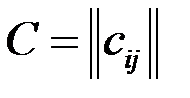 размера
размера 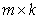 , у которой
, у которой
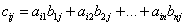 ,
, 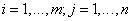
Пусть, 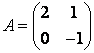
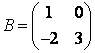
Тогда
 ,
,
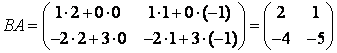 .
.
Определителем матрицы 2-го порядка называется число
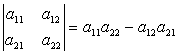 .
.
Например, 
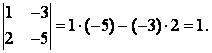
Найдем определители 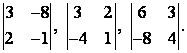
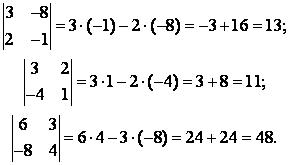
Определителем матрицы 3-го порядка называется число
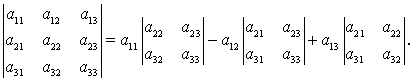
например,

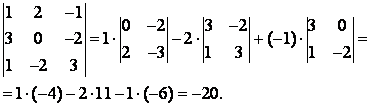
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Задача 1.
Для матриц  и
и  вычислить
вычислить
a) 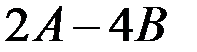
b) 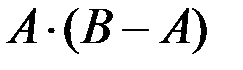
c) 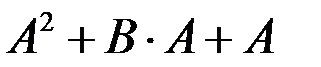
Вариант 0. 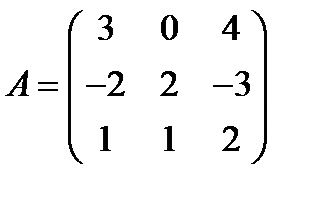 ,
, 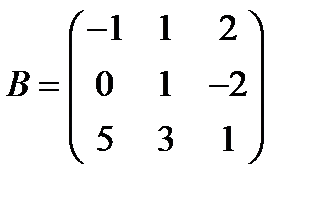 .
.
Вариант 1. 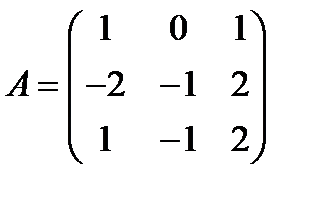 ,
, 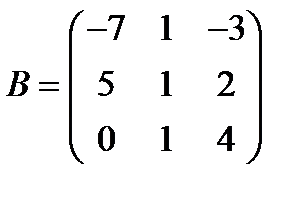 .
.
Вариант 2. 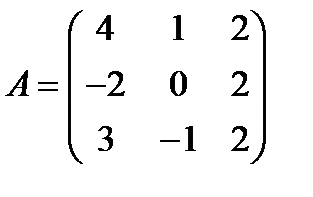 ,
, 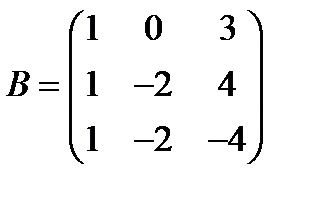 .
.
Вариант 3. 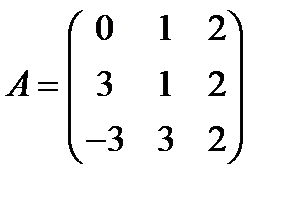 ,
, 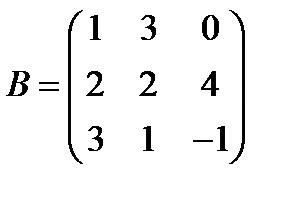 .
.
Вариант 4. 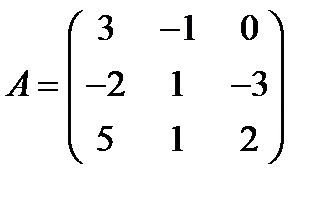 ,
, 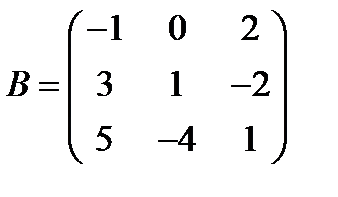 .
.
Вариант 5. 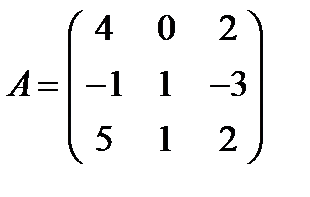 ,
, 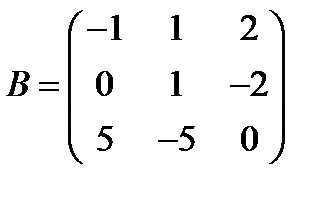 .
.
Вариант 6. 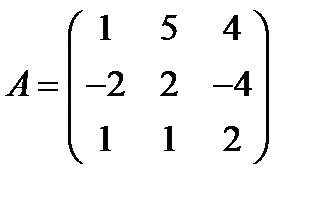 ,
, 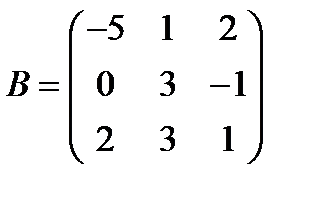 .
.
Вариант 7. 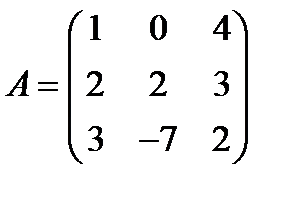 ,
, 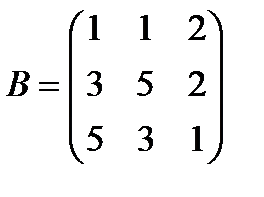
Вариант 8. 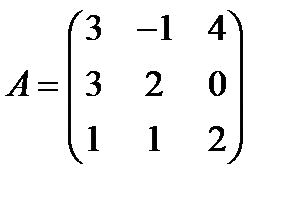 ,
, 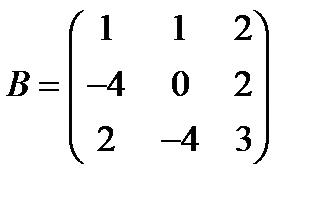 .
.
Вариант 9. 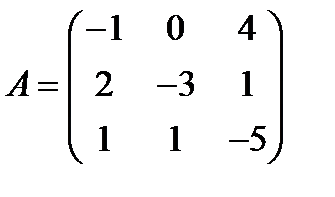 ,
,  .
.
Задача 2.
Вычислить определители
а) второго порядка;
б) третьего порядка
Вариант 0. а) 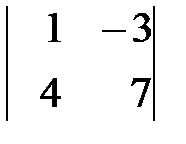 , б)
, б) 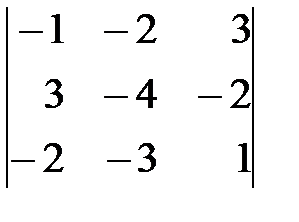 .
.
Вариант 1. а) 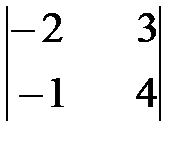 , б)
, б) 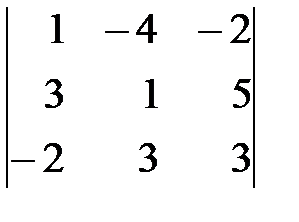 .
.
Вариант 2. а) 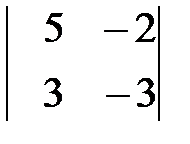 , б)
, б) 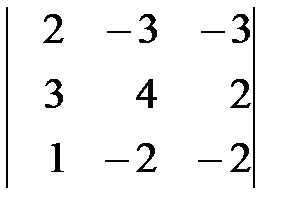 .
.
Вариант 3. а) 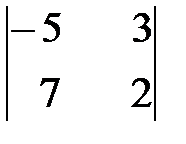 , б)
, б) 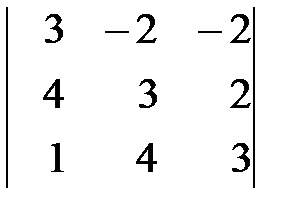 .
.
Вариант 4. а) 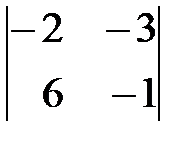 , б)
, б) 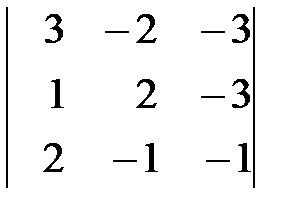 .
.
Вариант 5. а) 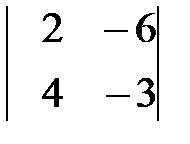 , б)
, б) 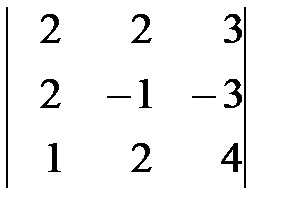 .
.
Вариант 6. а)  , б)
, б) 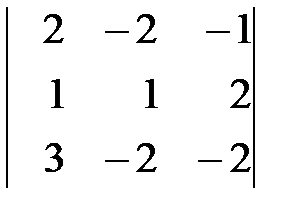 .
.
Вариант 7. а) 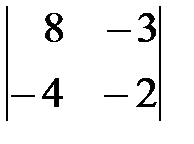 , б)
, б) 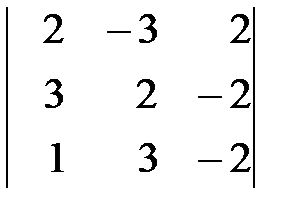 .
.
Вариант 8. а) 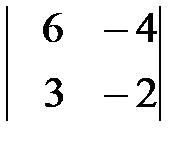 , б)
, б) 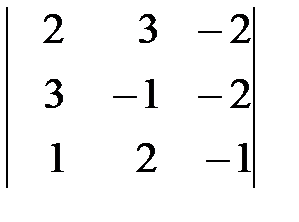 .
.
Вариант 9. а) 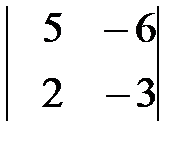 , б)
, б) 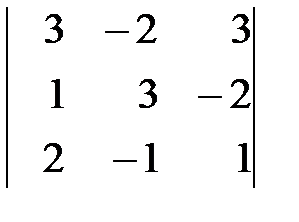 .
.
СИСТЕМЫЛИНЕЙНЫХ УРАВНЕНИЙ
ПРАКТИЧЕСКАЯ ЧАСТЬ
Пример 1. Решить систему трех уравнений с тремя неизвестными:
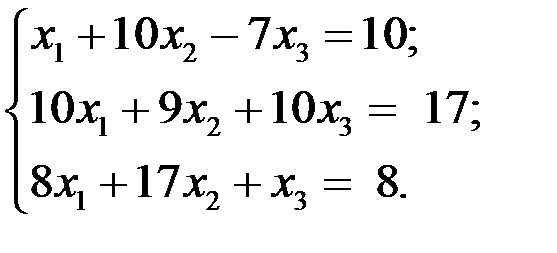
Найдем решение:
а) методом Гаусса последовательных исключений неизвестных;
б) по формуле 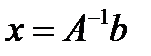 с вычислением обратной матрицы
с вычислением обратной матрицы 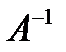 ;
;
в) по формулам Крамера.
Решение. а) Начнем с метода Гаусса последовательных исключений неизвестных. Сначала нужно преобразовать систему уравнений так, чтобы переменная 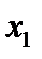 осталась только в одном уравнении системы, например, в первом. Затем уравнение, в которое входит
осталась только в одном уравнении системы, например, в первом. Затем уравнение, в которое входит 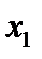 , отбрасывают, и рассматривают систему из оставшихся уравнений, в котором число уравнений и число неизвестных уменьшилось. Эту редуцированную систему преобразуют так, чтобы переменная
, отбрасывают, и рассматривают систему из оставшихся уравнений, в котором число уравнений и число неизвестных уменьшилось. Эту редуцированную систему преобразуют так, чтобы переменная 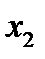 осталась только в одном уравнении. Затем уравнение, в которое входит
осталась только в одном уравнении. Затем уравнение, в которое входит 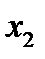 , отбрасывают, и вновь рассматривают систему из меньшего числа уравнений. Преобразования с последовательным исключением неизвестных
, отбрасывают, и вновь рассматривают систему из меньшего числа уравнений. Преобразования с последовательным исключением неизвестных 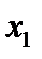 ,
, 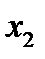 ,
, 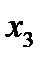 и т.д. продолжают до тех пор, пока к каждой неизвестной не будет применена процедура исключения. После этого значения
и т.д. продолжают до тех пор, пока к каждой неизвестной не будет применена процедура исключения. После этого значения 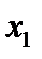 ,
, 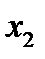 ,
, 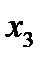 ,… определяют сначала из последнего уравнения, затем из предпоследнего и т.д., вплоть до первого уравнения.
,… определяют сначала из последнего уравнения, затем из предпоследнего и т.д., вплоть до первого уравнения.
Итак, возьмем первое уравнение системы и с его помощью исключим переменную 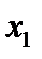 из второго и третьего уравнений. Для этого первое уравнение перепишем без изменений, а второе и третье уравнения сложим с подходящими коэффициентами с первым уравнений системы. Сначала умножим первое уравнение системы на 10, второе - на
из второго и третьего уравнений. Для этого первое уравнение перепишем без изменений, а второе и третье уравнения сложим с подходящими коэффициентами с первым уравнений системы. Сначала умножим первое уравнение системы на 10, второе - на 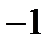 , а затем сложим полученные уравнения. Получим
, а затем сложим полученные уравнения. Получим
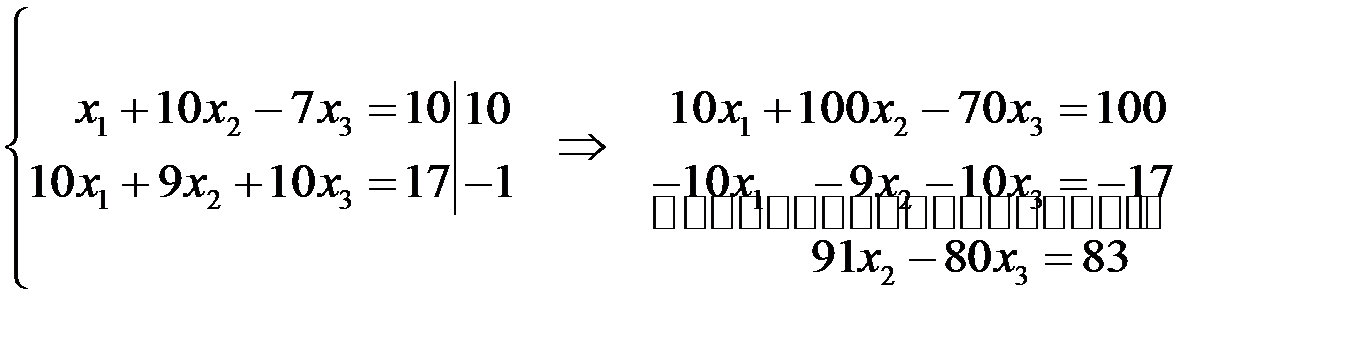
Аналогично, умножим первое уравнение системы на 8, второе - на 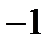 , а затем сложим.
, а затем сложим.
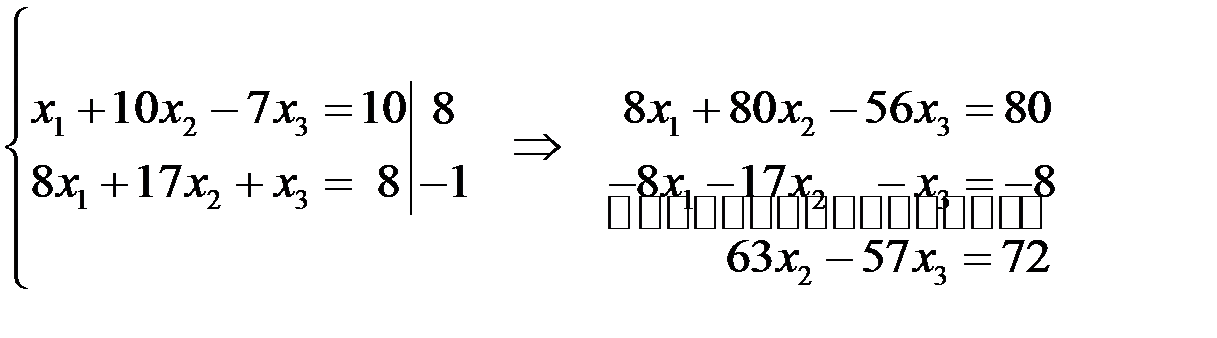
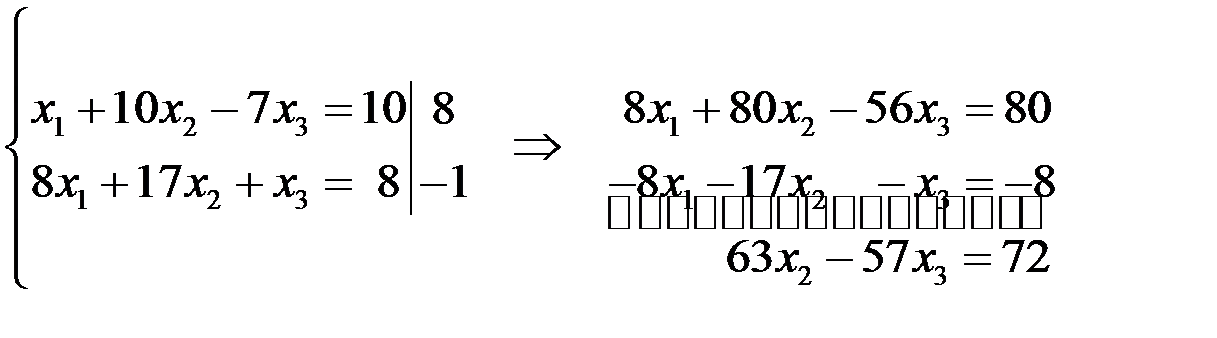
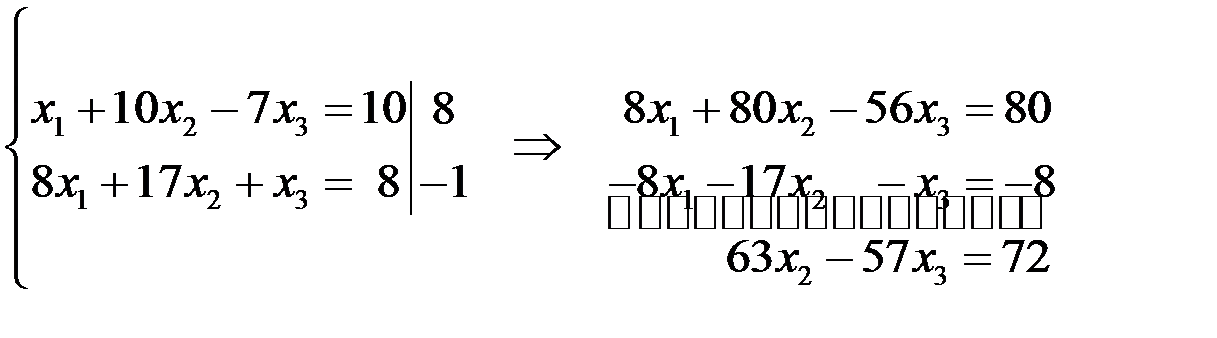
Данное преобразование будем записывать в следующем виде:
 Û
Û 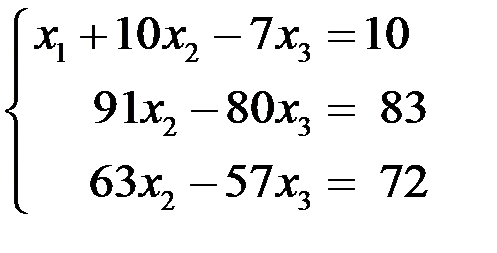
Возьмем теперь второе уравнение и с его помощью исключим переменную 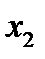 из третьего уравнения системы. Для этого второе уравнение системы умножим на 63, третье уравнение умножим на
из третьего уравнения системы. Для этого второе уравнение системы умножим на 63, третье уравнение умножим на 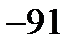 , и сложим полученные уравнения.
, и сложим полученные уравнения.
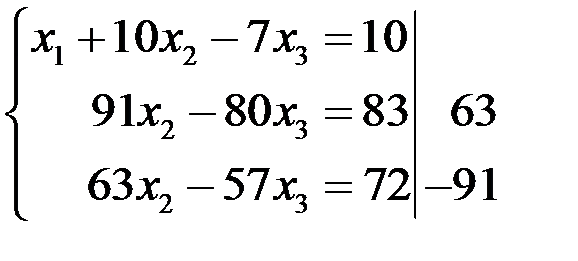 Û
Û 
Мы привели систему уравнений к так называемому верхне-треугольному виду. Теперь методом обратного хода можно определить сначала значение переменной 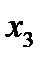 из последнего уравнения системы, затем значение переменной
из последнего уравнения системы, затем значение переменной 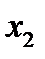 из второго уравнения, и, наконец, значение переменной
из второго уравнения, и, наконец, значение переменной 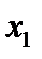 из первого уравнения.
из первого уравнения.
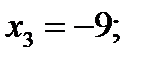
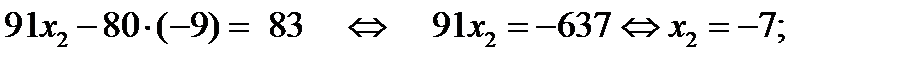
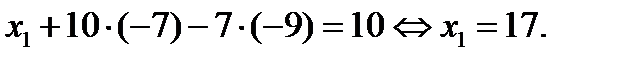
Ответ: 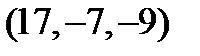 .
.
б) Решим теперь ту же систему уравнений матричным способом, с вычислением обратной матрицы.
Как вычислять определитель 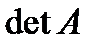 и как находить обратную матрицу
и как находить обратную матрицу 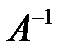 , будет объяснено ниже.
, будет объяснено ниже.
Используя правило умножения 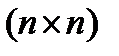 -матрицы и вектор-столбца размера
-матрицы и вектор-столбца размера 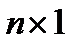 , запишем исходную систему линейных уравнений в виде
, запишем исходную систему линейных уравнений в виде
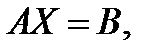
где
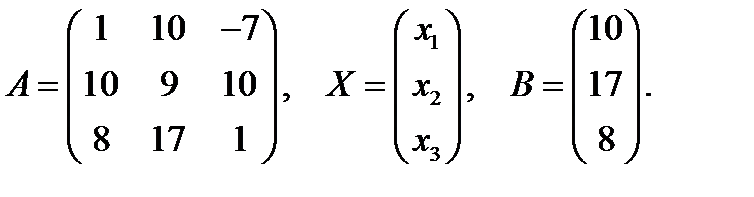
Поскольку по определению обратной матрицы 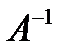 имеем
имеем
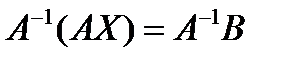 Û
Û 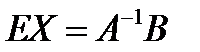 ,
,
и так как 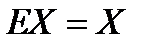 , решение системы можно записать в виде
, решение системы можно записать в виде
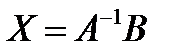 .
.
где 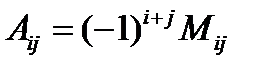 – алгебраические дополнения элементов
– алгебраические дополнения элементов 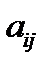 матрицы
матрицы 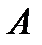 (заметим, что алгебраические дополнения элементов строк записываются в соответствующие столбцы). Получаем:
(заметим, что алгебраические дополнения элементов строк записываются в соответствующие столбцы). Получаем:
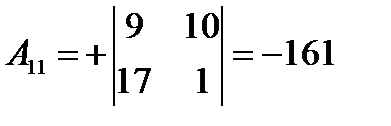 ,
, 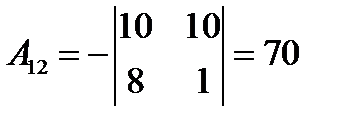 ,
, 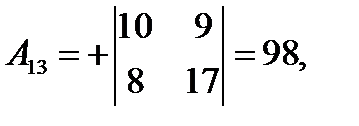
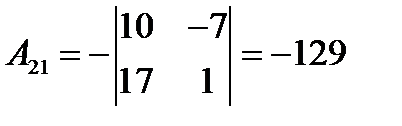 ,
, 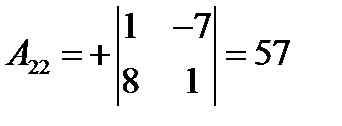 ,
, 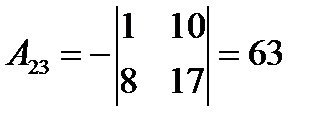 ,
,
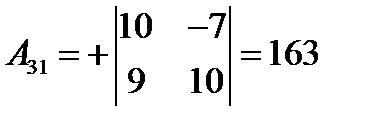 ,
, 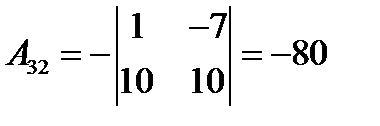 ,
, 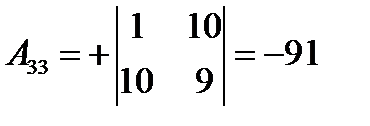 .
.
Обратная матрица, следовательно, имеет вид
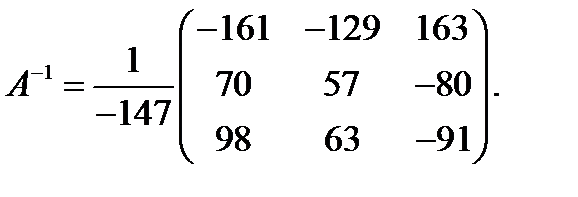
Остается умножить матрицу 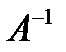 на столбец
на столбец  ,
,
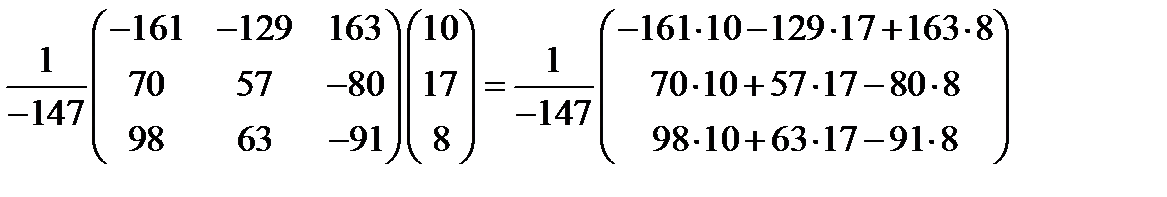
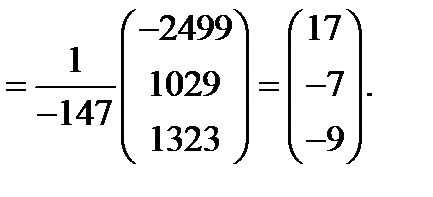
Результаты совпали.
в) Рассмотрим третий способ решения систем линейных уравнений, который является непосредственным следствием матричной формулы 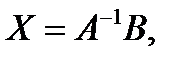 ¾ правило Крамера.
¾ правило Крамера.
Обозначим через  определитель матрицы
определитель матрицы 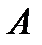 . Пусть
. Пусть 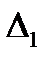 есть определитель матрицы
есть определитель матрицы 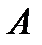 , в которой вместо первого столбца стоит столбец
, в которой вместо первого столбца стоит столбец 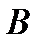 . Пусть
. Пусть 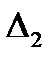 есть определитель матрицы
есть определитель матрицы 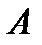 , в которой вместо второго столбца стоит столбец
, в которой вместо второго столбца стоит столбец 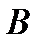 . Наконец, пусть
. Наконец, пусть 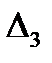 есть определитель матрицы
есть определитель матрицы 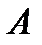 , в которой вместо третьего столбца стоит столбец
, в которой вместо третьего столбца стоит столбец 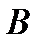 .
.
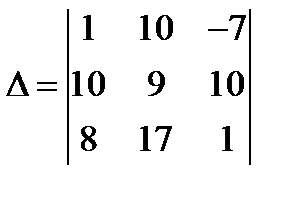 ,
,
 ,
, 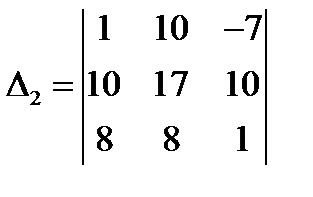 ,
, 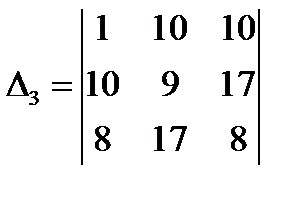
Если 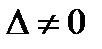 , то согласно правилу Крамера решение системы уравнений можно найти по формулам
, то согласно правилу Крамера решение системы уравнений можно найти по формулам
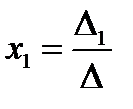 ,
, 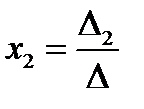 ,
, 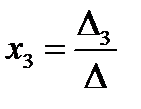 .
.
Имеем:
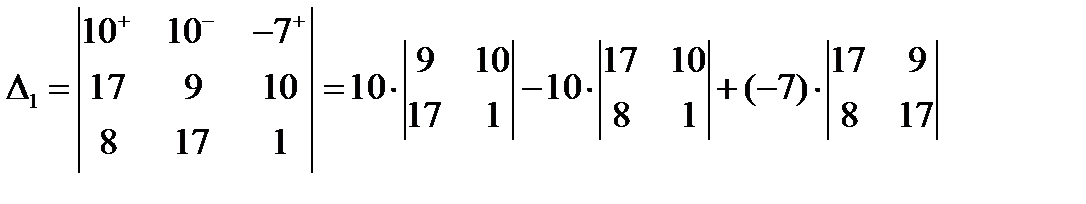
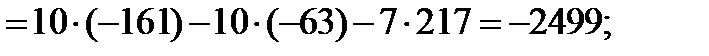
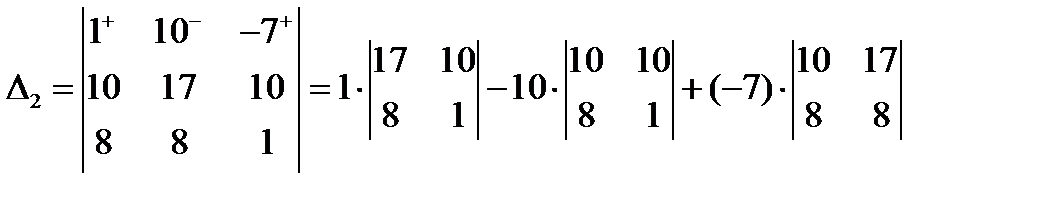


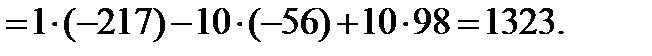
Следовательно, по формулам Крамера,
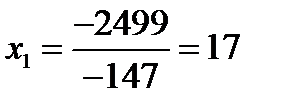 ,
, 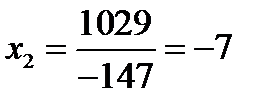 ,
, 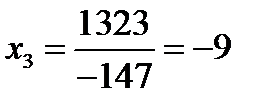 .
.
Ответы вновь совпали.
Пример 2. Решить систему уравнений
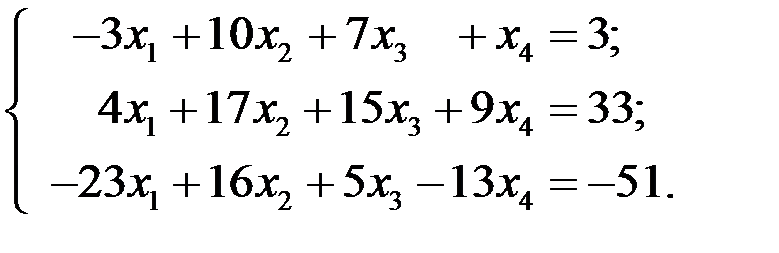
Решение. С помощью первого уравнения исключим переменную  из второго и третьего уравнений системы.
из второго и третьего уравнений системы.
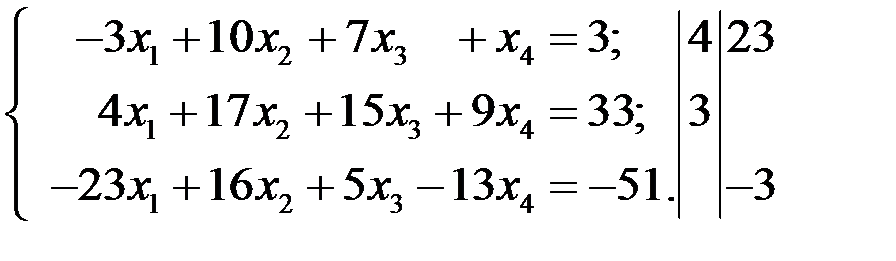
Получаем:
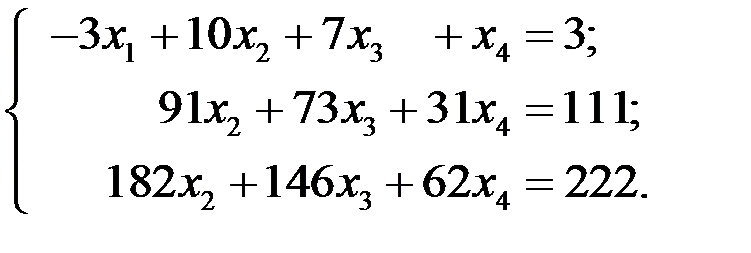
Исключим теперь с помощью второго уравнения системы переменную 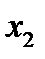 из третьего уравнения.
из третьего уравнения.
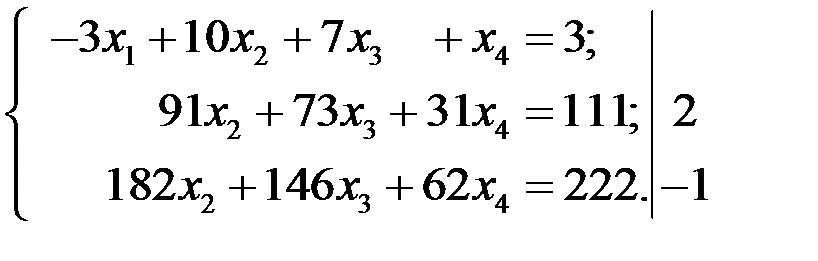
В результате третье уравнение системы превращается в тождеств
0 = 0, и остается только два уравнения:
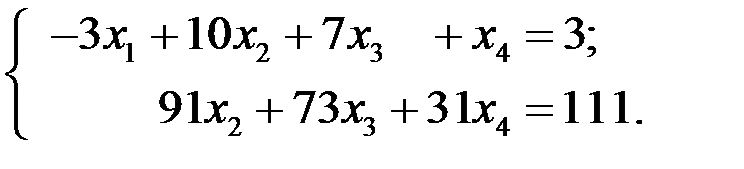
Мы привели систему к верхнетреугольному виду, однако для двух неизвестных (а именно, для 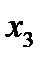 и для
и для  ) не хватило “своего” уравнения для преобразования исключения. В этом случае переменные
) не хватило “своего” уравнения для преобразования исключения. В этом случае переменные 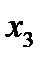 ,
,  объявляются свободными (то есть их значения могут выбираться произвольным образом), а значения остальных переменных (они называются базисными) могут быть выражены через значения свободных переменных.
объявляются свободными (то есть их значения могут выбираться произвольным образом), а значения остальных переменных (они называются базисными) могут быть выражены через значения свободных переменных.
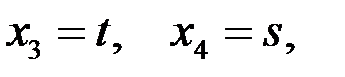

Отсюда:
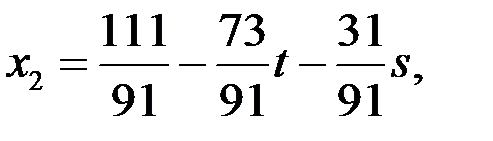
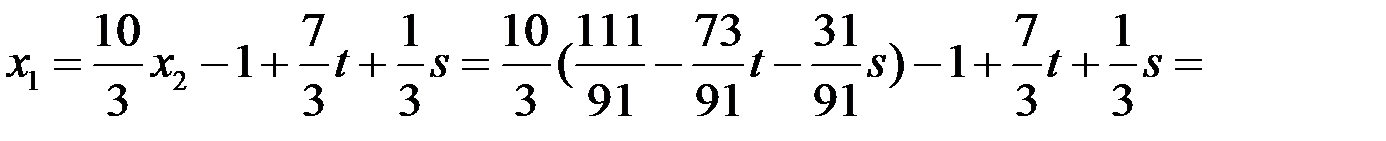
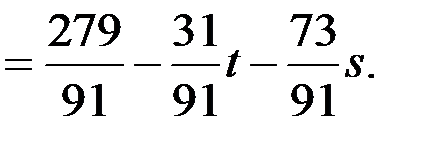
Ответ: 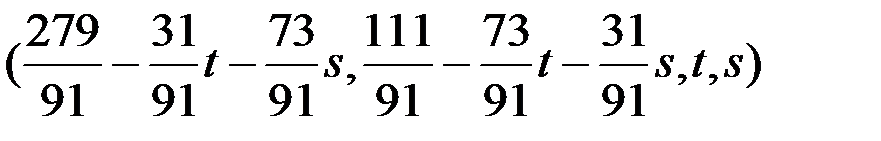 , где
, где  - произвольные параметры.
- произвольные параметры.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
1. Решить систему линейных уравнений тремя способами:
а) методом Гаусса последовательных исключений неизвестных;
б) по формуле 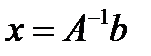 с вычислением обратной матрицы
с вычислением обратной матрицы 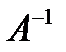 ;
;
в) по формулам Крамера.
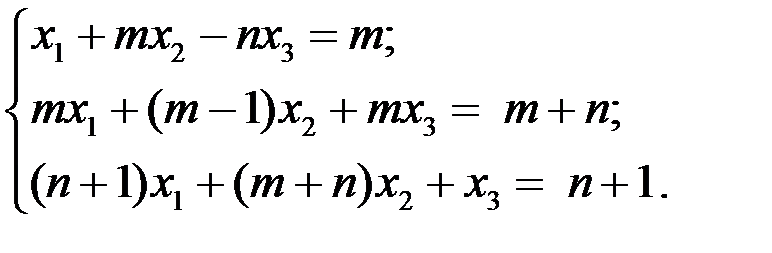
1. Решить методом Гаусса следующую вырожденную систему уравнений
2.
Значения параметров m и n, выбирается в соответствии с двумя последними цифрами зачетной книжки A и B.
Каждая задача зависит от двух числовых параметров m и n, которые определяются по цифрам A и B из таблиц:
| А | ||||||||||
| m |
| B | ||||||||||
| n |
ВЕКТОРНАЯ АЛГЕБРА
ПРАКТИЧЕСКАЯ ЧАСТЬ
Пример 1. Найти векторное произведение 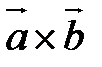 , если
, если 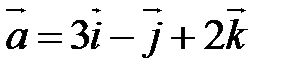 ,
, 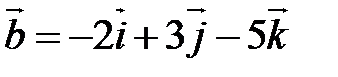 .
.
Решение. По формуле (2.1) получаем
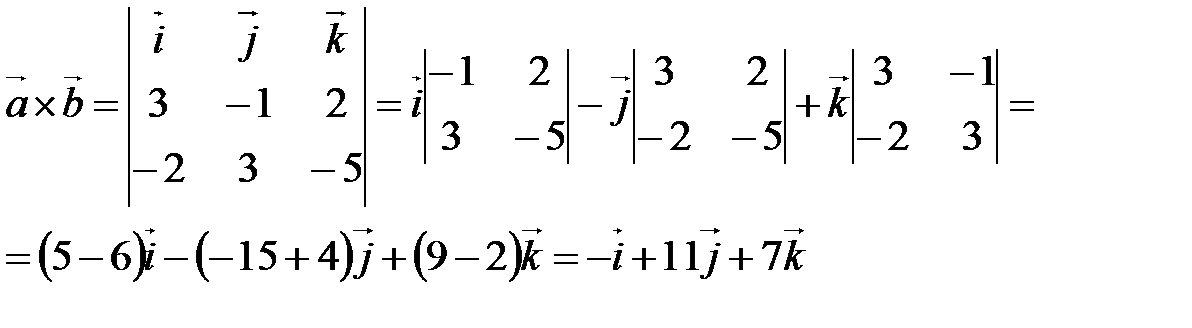 .
.
Пример 2. Вычислить площадь треугольника с вершинами А (7, 3, 4), В (1, 0, 6), С (4, 5, –2).
Решение. По формуле (2.3) имеем 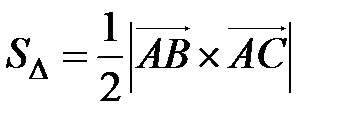 .
.
1) Найдем координаты векторов 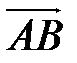 и
и  . Для этого вычтем из координат конца вектора координаты начала
. Для этого вычтем из координат конца вектора координаты начала
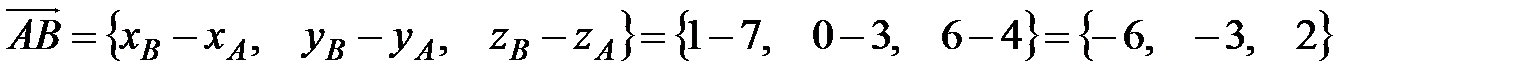
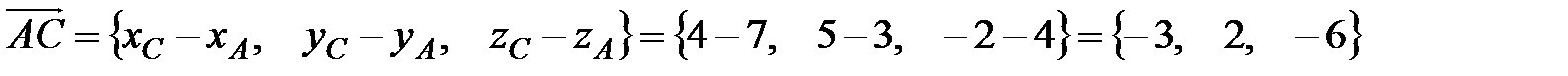
2) Найдем векторное произведение
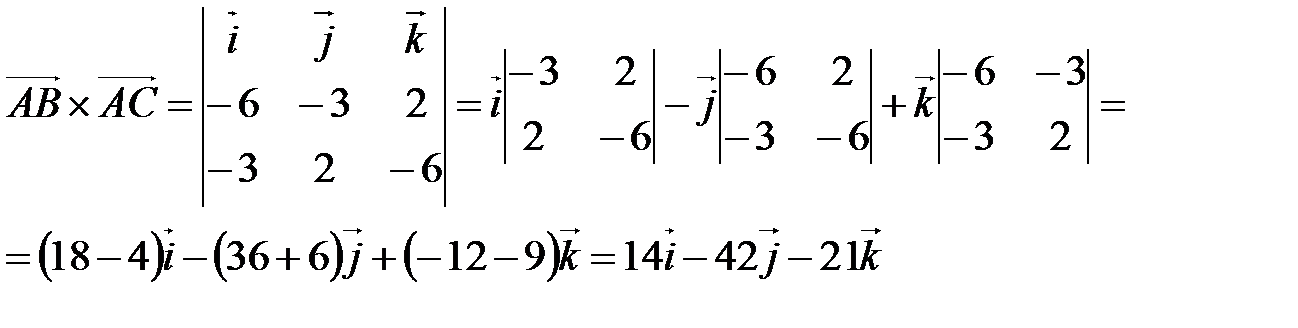
3) 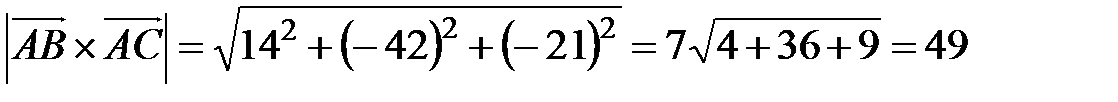
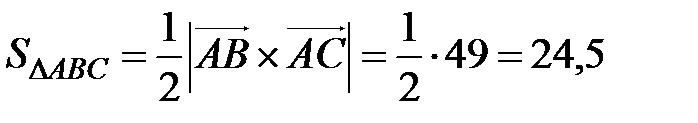 кв.ед.
кв.ед.
Пример 3. Сила 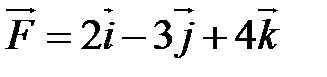 приложена к точке А (3, 4, –2). Найти ее момент М относительно точки О (4, 2, –1).
приложена к точке А (3, 4, –2). Найти ее момент М относительно точки О (4, 2, –1).
Решение. Находим вектор 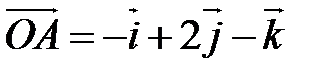 .
.
Искомый момент 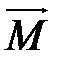 равен векторному произведению
равен векторному произведению 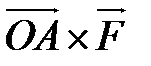
 .
.
Пример 4. Пирамида 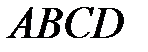 задана координатами вершин. Пользуясь понятиями и формулами векторной алгебры, найти:
задана координатами вершин. Пользуясь понятиями и формулами векторной алгебры, найти:
1) длину ребра 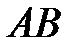 ;
;
2) угол между ребрами 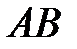 и
и 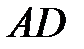 ;
;
3) площадь грани 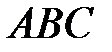 ;
;
4) объем пирамиды.
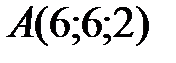 ,
, 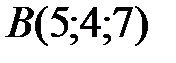 ,
, 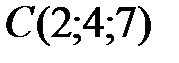 ,
, 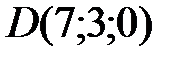 .
.
1) Решение. Координаты вектора 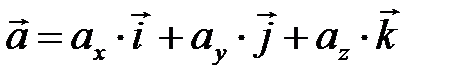 находятся по формулам:
находятся по формулам: 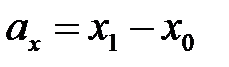 ,
, 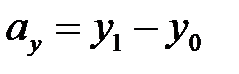 ,
, 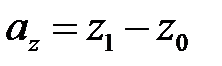 , где
, где 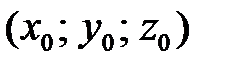 – координаты начала,
– координаты начала, 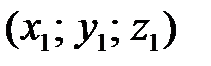 – координаты конца вектора
– координаты конца вектора 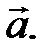 Тогда длина вектора
Тогда длина вектора 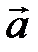 равна
равна 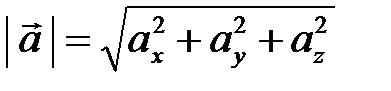 .
.
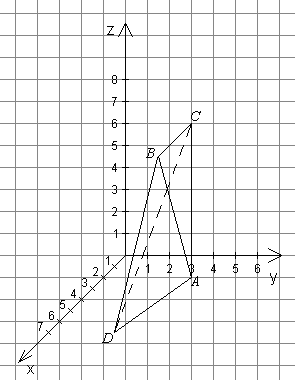
Рис. 2.22.
Рассмотрим вектор 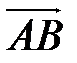 . Точка
. Точка 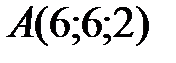 является началом, а точка
является началом, а точка 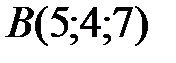 – концом вектора
– концом вектора 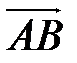 . Следовательно, вектор
. Следовательно, вектор 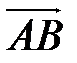 имеет следующие координаты:
имеет следующие координаты:
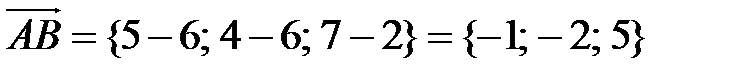 , а значит
, а значит
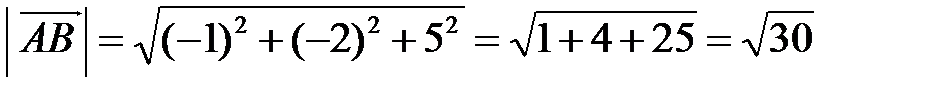 .
.
2) Косинус угла 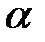 между векторами
между векторами 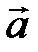 и
и 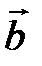 может быть найден по формуле:
может быть найден по формуле:
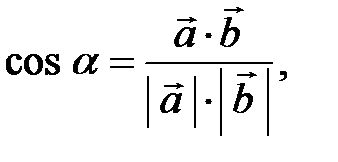 где
где 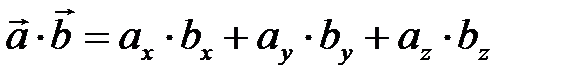 – скалярное произведение векторов
– скалярное произведение векторов 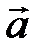 и
и 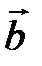 .
.
Для того, чтобы найти угол между ребрами 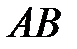 и
и 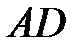 , введем в рассмотрение векторы
, введем в рассмотрение векторы 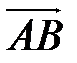 и
и 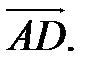 Так как координаты вектора
Так как координаты вектора 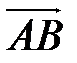 и его длина известны, определим координаты и длину вектора
и его длина известны, определим координаты и длину вектора 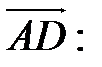
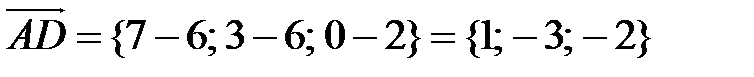 ,
,
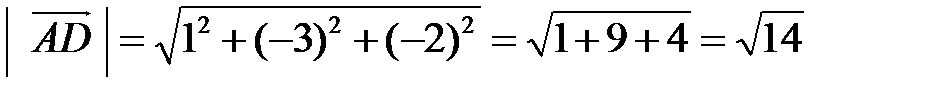 .
.
Тогда
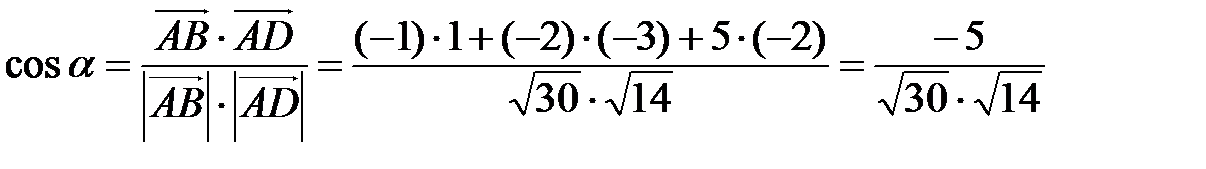
или 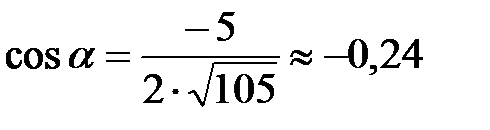 . Отсюда
. Отсюда 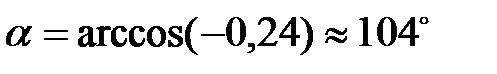 .
.
3) Площадь треугольника, построенного на векторах  и
и  , находится по формуле
, находится по формуле 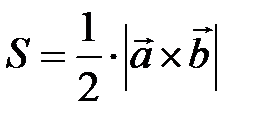 , через векторное произведение
, через векторное произведение
 .
.
Площадь грани 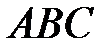 есть площадь треугольника
есть площадь треугольника 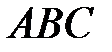 , построенного на векторах
, построенного на векторах 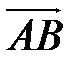 и
и 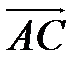 . Так как
. Так как 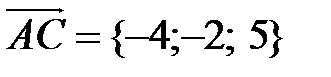 , тогда
, тогда
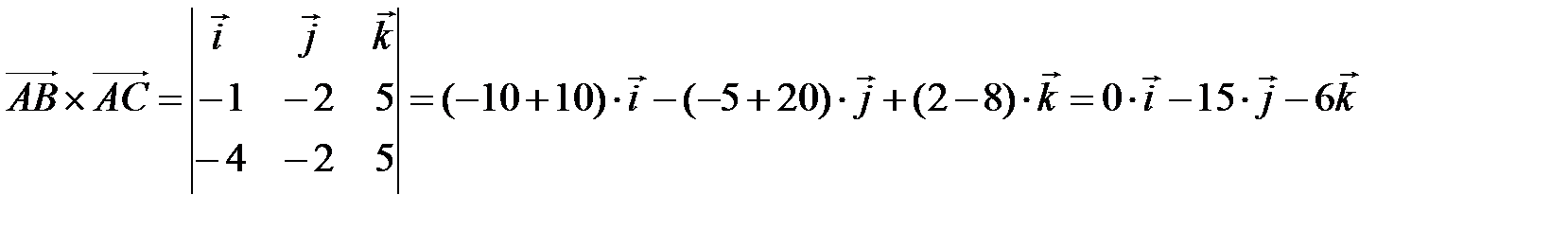 ,
,
а значит
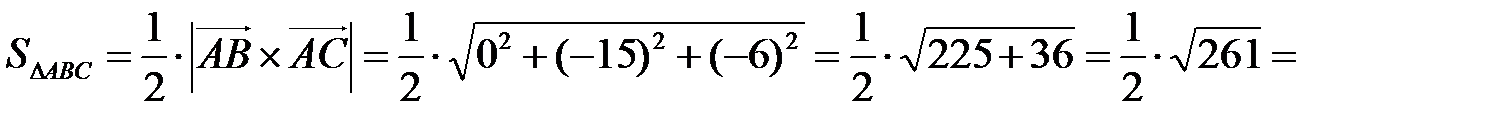
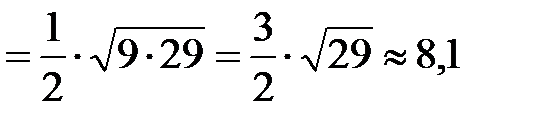 .
.
4) Объем 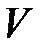 треугольной пирамиды, построенной на векторах
треугольной пирамиды, построенной на векторах 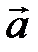 ,
, 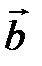 ,
, 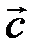 находится по формуле
находится по формуле 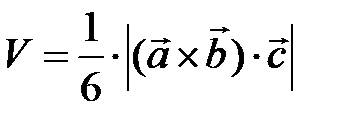 .
.
В нашем случае 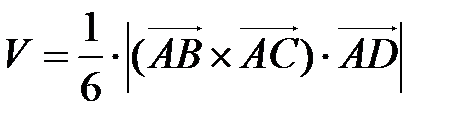 .
.
Так как 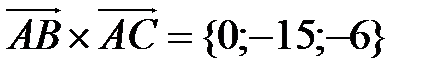 ,
, 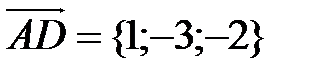 , получаем:
, получаем:
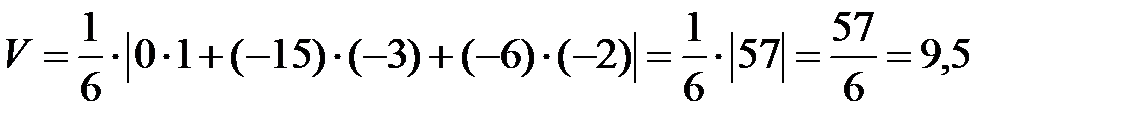 .
.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Задача. Пирамида 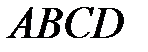 задана координатами вершин. Пользуясь понятиями и формулами векторной алгебры, найти:
задана координатами вершин. Пользуясь понятиями и формулами векторной алгебры, найти:
1) длину ребра 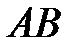 ;
;
2) угол между ребрами 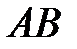 и
и 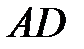 ;
;
3) площадь грани 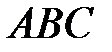 ;
;
4) объем пирамиды.
Вариант 0. 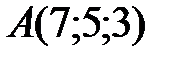 ,
, 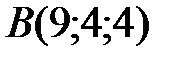 ,
, 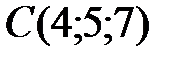 ,
, 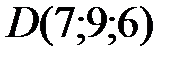 .
.
Вариант 1. 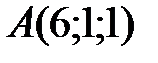 ,
, 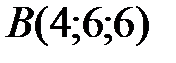 ,
, 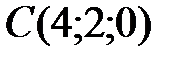 ,
, 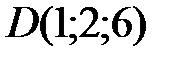 .
.
Вариант 2.  ,
, 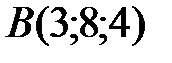 ,
, 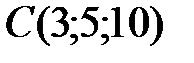 ,
, 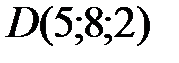 .
.
Вариант 3. 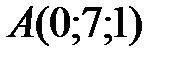 ,
, 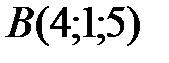 ,
, 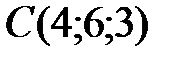 ,
, 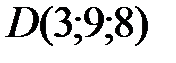 .
.
Вариант 4. 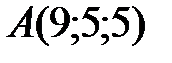 ,
, 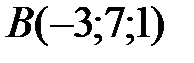 ,
,  ,
, 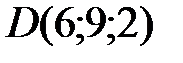 .
.
Вариант 5. 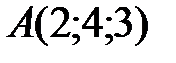 ,
, 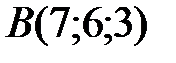 ,
, 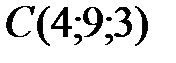 ,
, 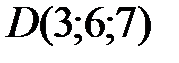 .
.
Вариант 6. 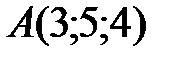 ,
, 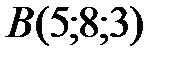 ,
, 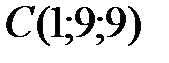 ,
, 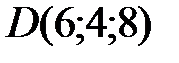 .
.
Вариант 7. 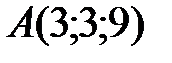 ,
, 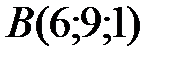 ,
, 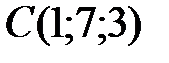 ,
, 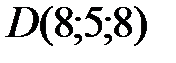 .
.
Вариант 8. 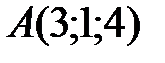 ,
, 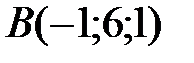 ,
, 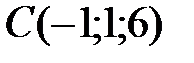 ,
, 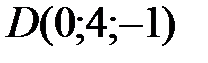 .
.
Вариант 9. 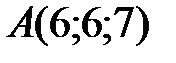 ,
, 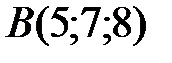 ,
, 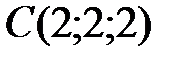 ,
, 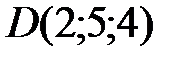 .
.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
ПРАКТИЧЕСКАЯ ЧАСТЬ
Пример 4.1. Составить уравнение прямой, проходящей через точку 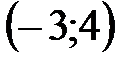 и наклоненной к оси
и наклоненной к оси  под углом
под углом 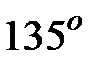 .
.
Решение. Уравнение прямой можно записать в форме (4.7). Здесь 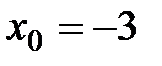 ,
, 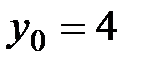 ,
, 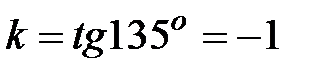 .
.
Следовательно, искомое уравнение будет
 или
или 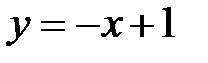 .
.
Пример 4.2. Составить уравнение прямой линии, проходящей через точки 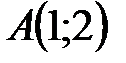 и
и 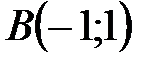 .
.
Решение. Подставляя в уравнение (4.9) 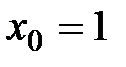 ,
, 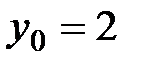 ,
, 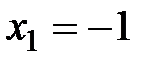 ,
, 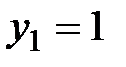 , получим
, получим 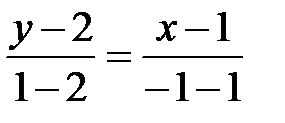 , откуда
, откуда 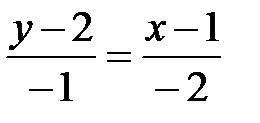 или
или 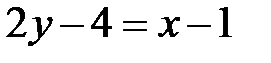
или окончательно 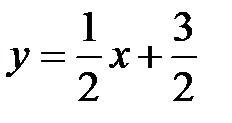 .
.
Пример 4.3. Найти угол между прямыми 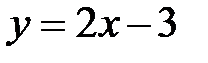 и
и 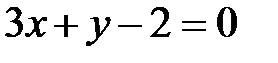 .
.
Решение. Если перенумеровать прямые в том порядке, как они заданы, то угловой коэффициент первой прямой будет 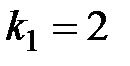 , а для второй прямой
, а для второй прямой 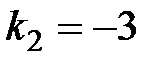 . Тогда по формуле (4.11) получим
. Тогда по формуле (4.11) получим
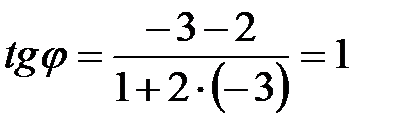 , откуда
, откуда 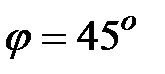 .
.
Пример 4.4. Доказать, что прямые 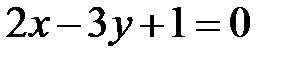 и
и  параллельны.
параллельны.
Решение. В самом деле, угловые коэффициенты этих прямых 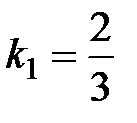 ,
, 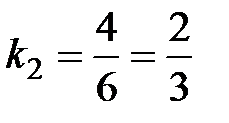 , т.е. условие параллельности выполнено.
, т.е. условие параллельности выполнено.
Пример 4.5. При каком значении  уравнение
уравнение  определяет прямую, перпендикулярную к прямой
определяет прямую, перпендикулярную к прямой 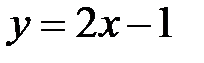 ?
?
Решение. Угловой коэффициент второй прямой 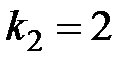 . Условие перпендикулярности дает
. Условие перпендикулярности дает 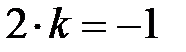 , откуда
, откуда 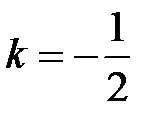 .
.
Пример 4.6. Найти уравнение прямой, проходящей через точку 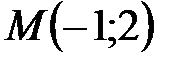 параллельно прямой
параллельно прямой 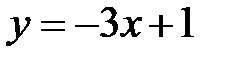 .
.
Решение. Искомая прямая по условию параллельна данной прямой. Следовательно, угловой коэффициент искомой прямой 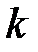 равен угловому коэффициенту данной прямой:
равен угловому коэффициенту данной прямой: 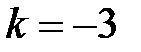 . Пользуясь уравнением (1.7) прямой, проходящей через данную точку, и учитывая, что в этом уравнении следует положить
. Пользуясь уравнением (1.7) прямой, проходящей через данную точку, и учитывая, что в этом уравнении следует положить 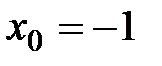 ,
, 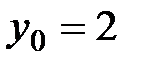 и
и 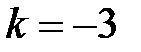 , получаем
, получаем 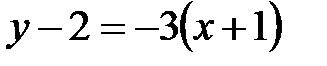 или
или
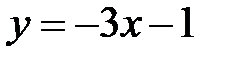 .
.
Пример 4.7. Составить уравнение прямой, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой 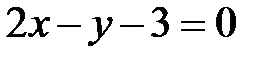 .
.
Решение. Уравнение данной прямой можно записать в форме 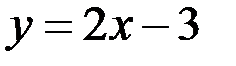 , откуда следует, что ее угловой коэффициент
, откуда следует, что ее угловой коэффициент  . Угловой коэффициент
. Угловой коэффициент 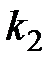 искомой прямой, перпендикулярной к данной, связан с коэффициентом
искомой прямой, перпендикулярной к данной, связан с коэффициентом 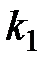 условием
условием  . Следовательно,
. Следовательно, 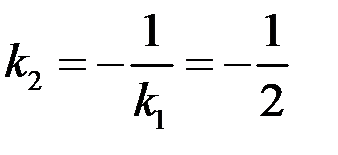 . Теперь остается воспользоваться уравнением (4.7) прямой, проходящей через данную точку, положив в нем
. Теперь остается воспользоваться уравнением (4.7) прямой, проходящей через данную точку, положив в нем 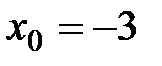 ,
, 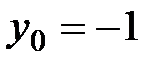 и
и 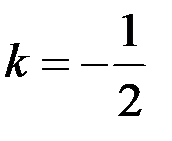 :
:
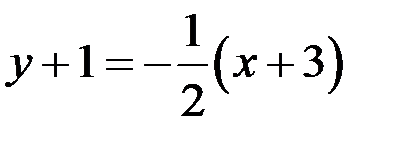 .
.
После упрощений получим
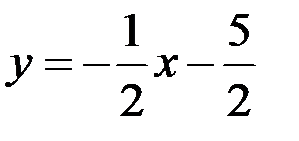 .
.
Пример 4.8. Найти расстояние от точки 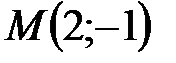 до прямой
до прямой 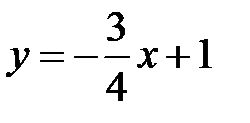 .
.
Решение. Запишем уравнение данной прямой в общем виде:
 ,
,
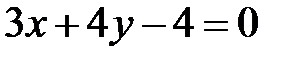 .
.
Воспользуемся уравнением (4.19) для вычисления расстояние от точки до прямой 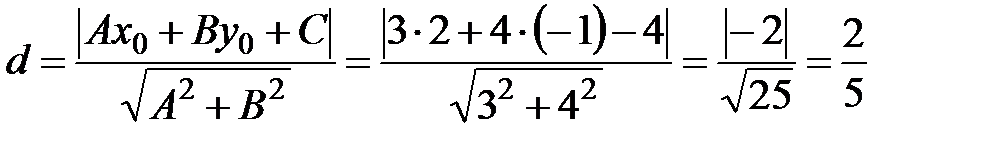 .
.
Пример 4.9. Треугольник 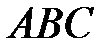 задан координатами вершин. Найти:
задан координатами вершин. Найти:
1) длину стороны 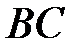 ;
;
2) уравнения сторон треугольника;
3) уравнение высоты, проведенной из вершины 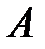 ;
;
4) угол 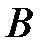 в радианах с точностью до 0,01;
в радианах с точностью до 0,01;
5) уравнение прямой, проходящей через вершину  параллельно прямой
параллельно прямой 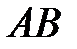 .
.
Сделать чертеж.
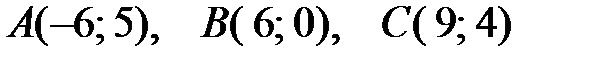 .
.
Решение.
1) Длину стороны 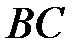 найдем по формуле (4.15) расстояния между двумя заданными точками
найдем по формуле (4.15) расстояния между двумя заданными точками 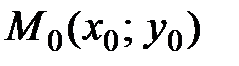 и
и  :
:
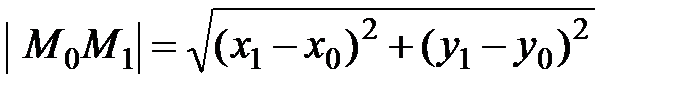 .
.
Так как 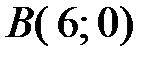 и
и 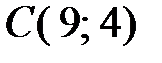 , получаем
, получаем
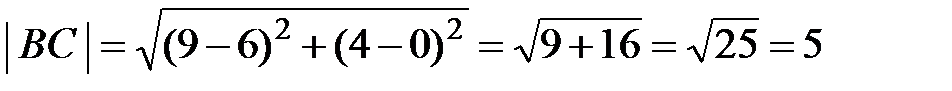 .
.
2) Для нахождения уравнений сторон треугольника, воспользуемся уравнением (4.9) прямой, проходящей через две заданные точки 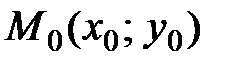 и
и 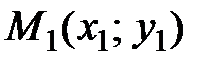 :
:
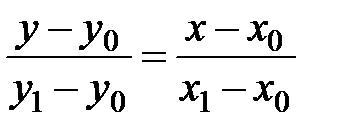 .
.
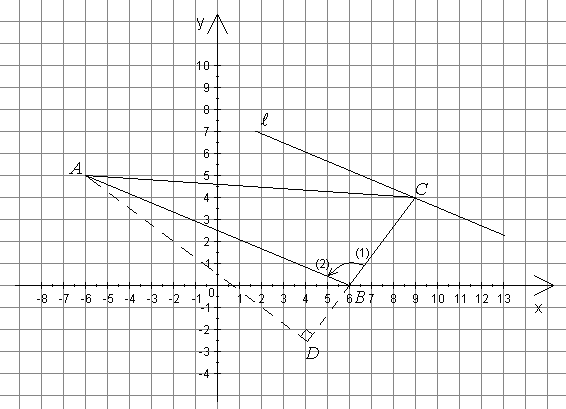
Рис. 4.8
Так как 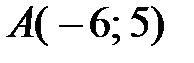 ,
, 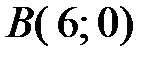 , то уравнение стороны
, то уравнение стороны 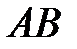 имеет вид
имеет вид 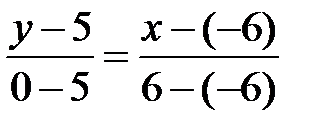 , или, после упрощения
, или, после упрощения 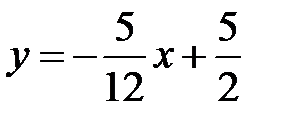 .
.
Аналогично находим уравнения сторон 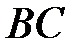 и
и 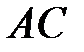 .
.
Уравнение 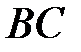 :
: 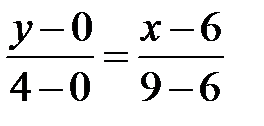 или
или 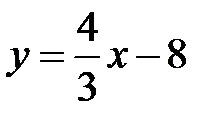 .
.
Уравнение 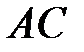 :
: 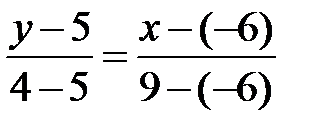 или
или 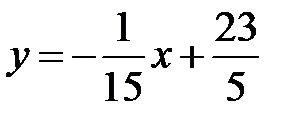 .
.
3) Высота, проведенная из вершины 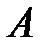 , есть отрезок прямой, которая перпендикулярна
, есть отрезок прямой, которая перпендикулярна 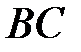 .
.
Из формул (4.7) и (4.14) следует, что уравнение высоты 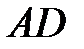 имеет вид:
имеет вид:
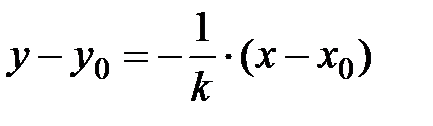 , где
, где  – координаты точки
– координаты точки 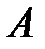 ;
; 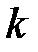 – угловой коэффициент прямой
– угловой коэффициент прямой 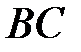 . Из полученного в пункте 2 уравнения
. Из полученного в пункте 2 уравнения 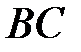 находим, что
находим, что  . По условию
. По условию 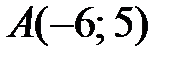 , тогда
, тогда 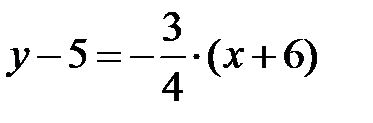 или
или