Итак, решением стационарного уравнения Шрёдингера для одномерного гармонического осциллятора является следующая пси-функция:
,
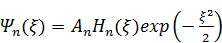где Hn (x) – это полиномы ЭрмитаHn (x), а множитель A –это произвольная константа.
В справочниках по математике полиномы Эрмита определяются следующей формулой:
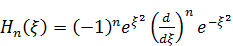. (4)
Выясним для примера, какими являются первые два полинома Эрмита.
.
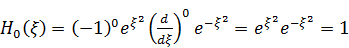Получили константу. Естественно, ведь полином нулевой степени – это и есть константа. Далее:
.
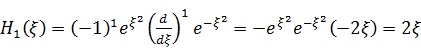Получили линейную функцию, то есть полином первой степени.
Остальные полиномы Эрмита можно находить не по формуле (4), а проще: используя так называемую рекуррентную формулу:
.
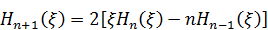Получите по этой формуле самостоятельно ещё парочку полиномов Эрмита. Результат должен получиться таким:
, 
.
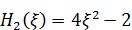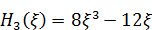Произвольный множитель пси-функции An находят, естественно, из условия нормировки
.
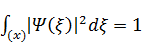В результате использования этого условия, то есть после интегрирования, получается:
,
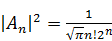Итак, пси-функции стационарных состояний линейного[1] осциллятора для всех уровней энергии мы знаем. Что это нам даёт? – В первую очередь, функцию распределения координат частицы
.
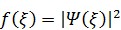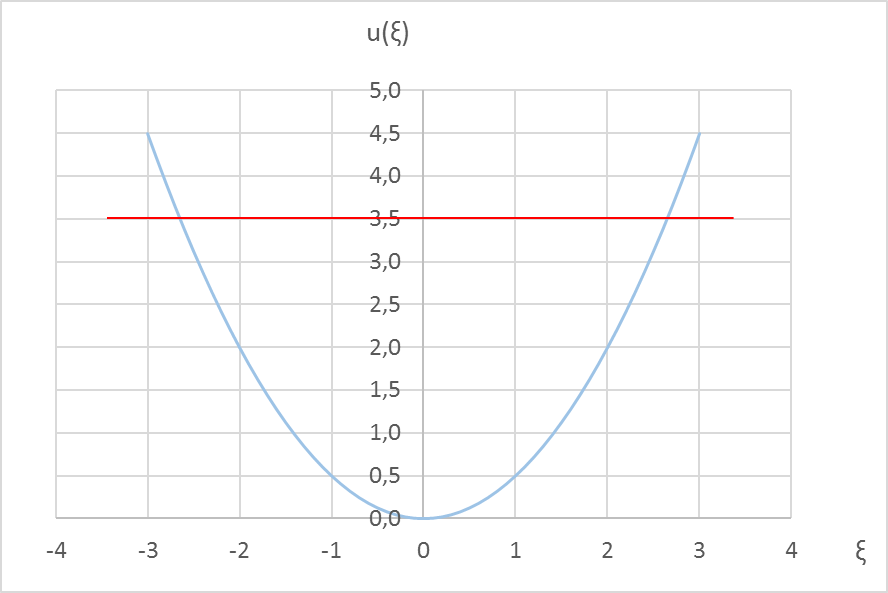
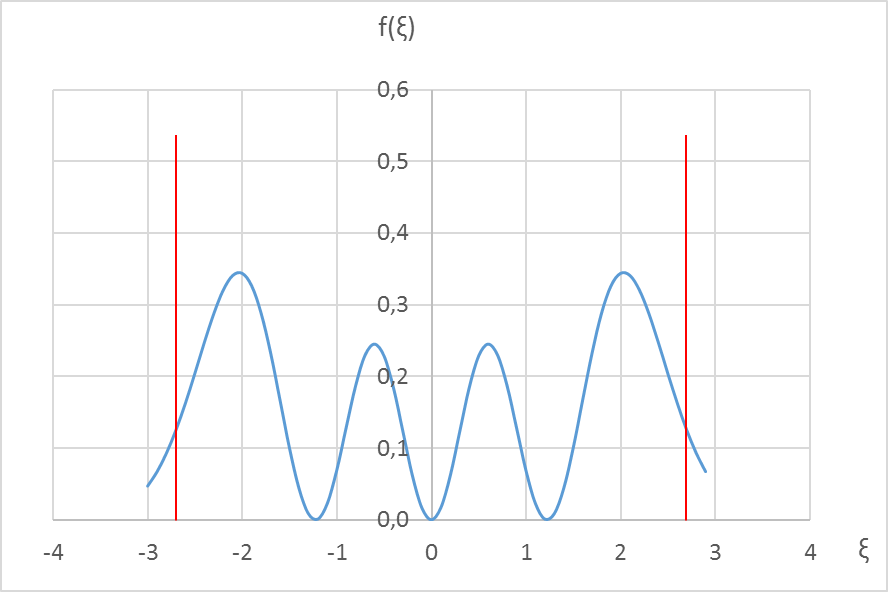
На рисунках приведены графики функций f (x) для четырёх первых стационарных состояний – основного (n = 0) и трёх возбуждённых (n = 1, n = 2 и n = 3). При расчётах функций распределения использованы выражения для первых четырёх полиномов Эрмита.
Для каждого из состояний (уровней) приведены два графика.
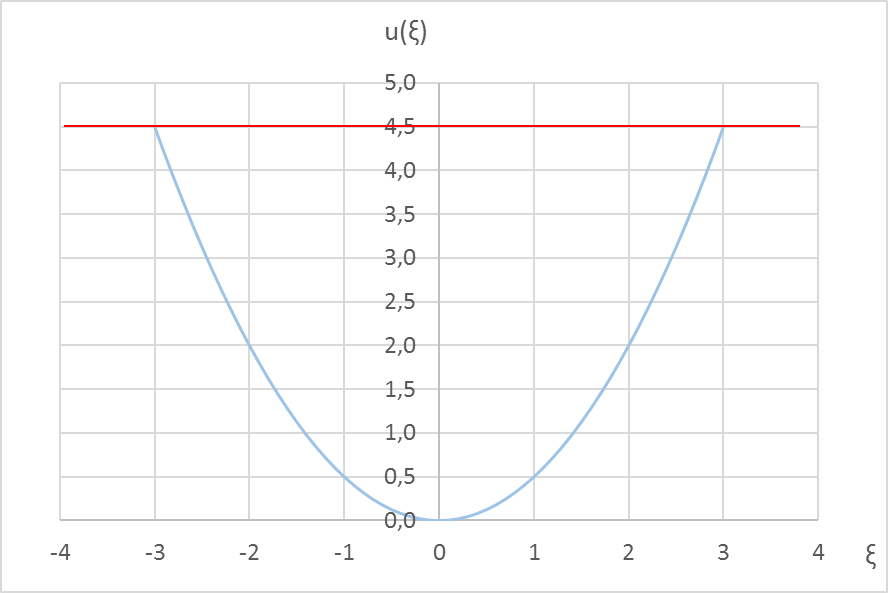
Слева – график потенциальной энергии в тех же относительных единицах, что и энергия: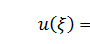 
, то есть яма, и энергетический уровень в виде красной горизонтальной линии.
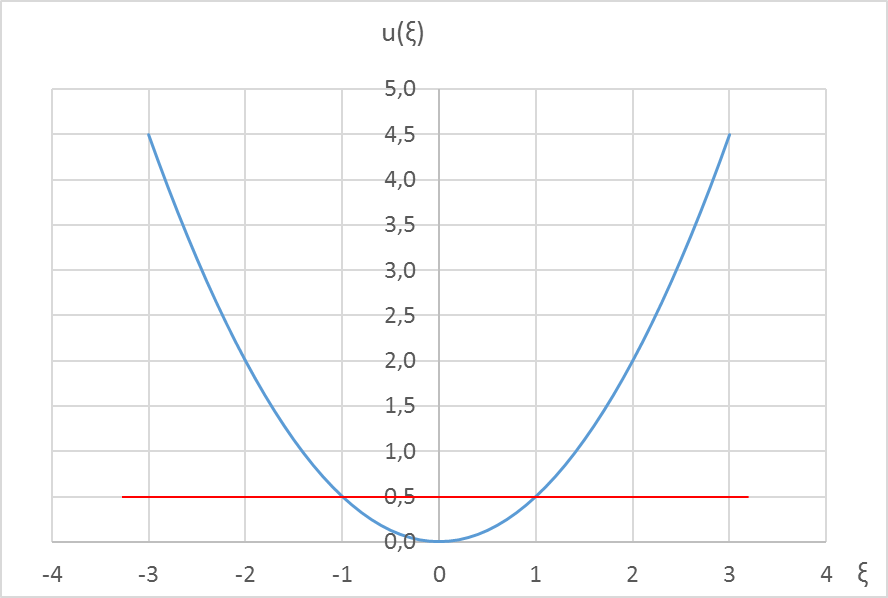
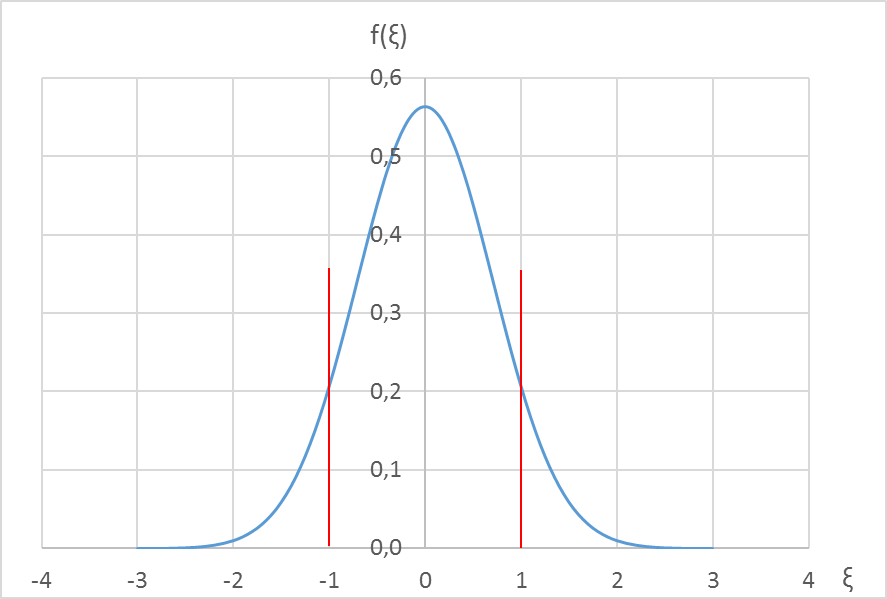
| n = 0 – основное состояние |
Справа – график функции распределения координаты частицы f (x) и границы классически доступной области в виде красных вертикальных линий.
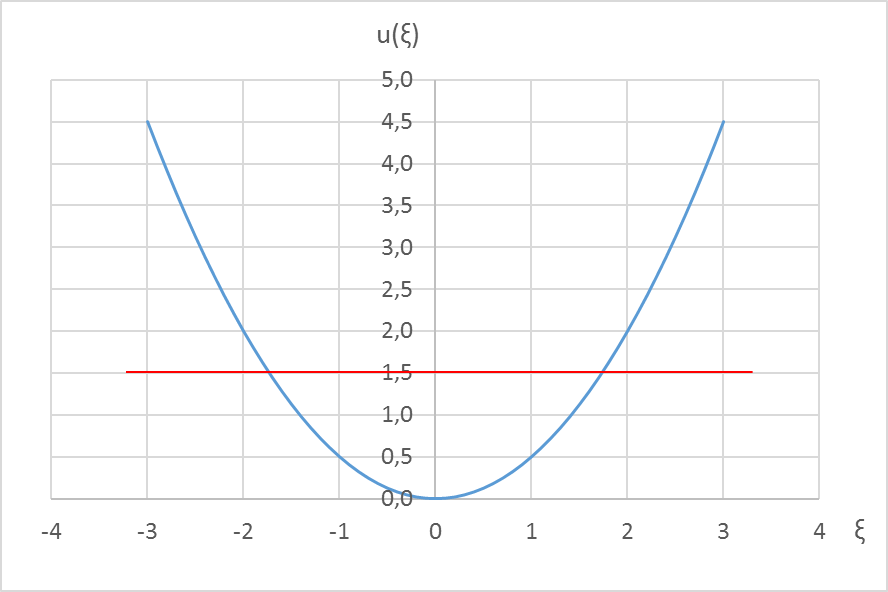
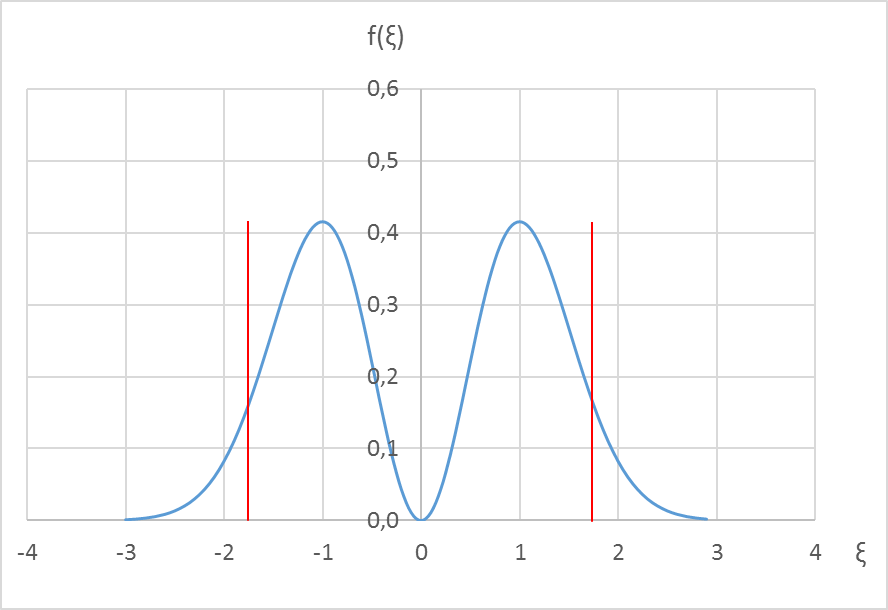
| n = 1 – первое возбуждённое состояние |
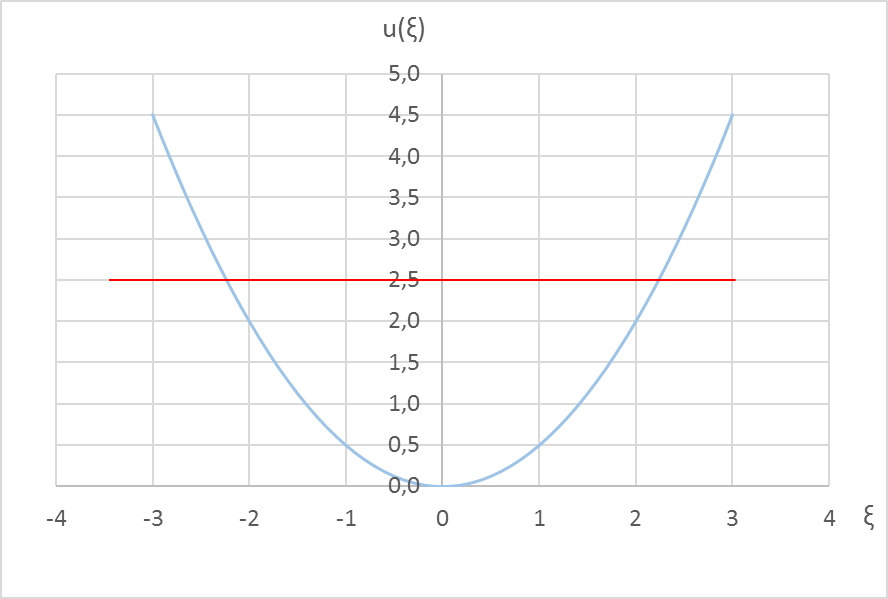
| n = 2 – второе возбуждённое состояние |
| n = 3 – третье возбуждённое состояние |
| n = 4 – четвёртое возбуждённое состояние |
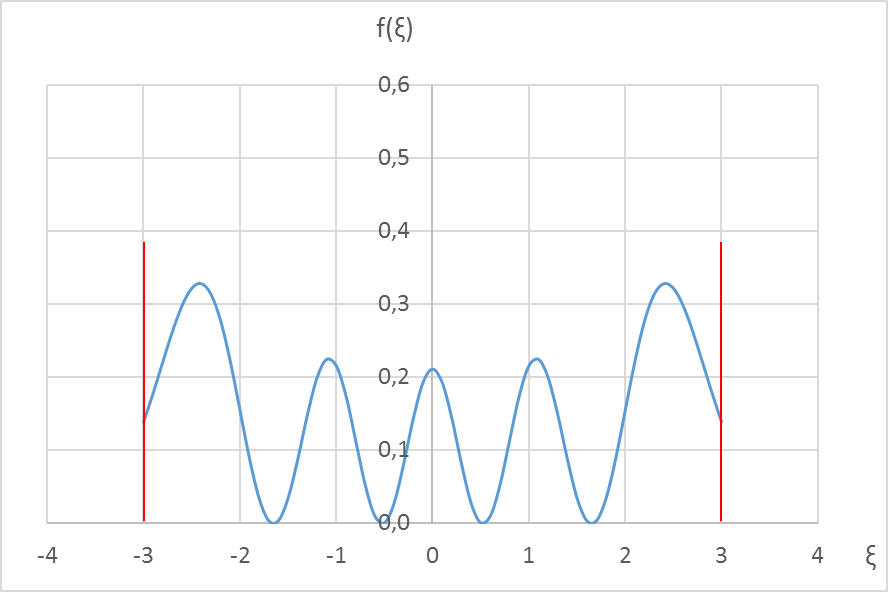
Выводы, которые следуют из графиков, таковы.
1). Классический одномерный осциллятор в процессе колебаний быстро проскакивает положение равновесия (точку x = 0), но при подходе к точкам поворота постепенно замедляется, поэтому большую часть времени пребывает именно в окрестности точек поворота. Квантовый осциллятор в основном состоянии ведёт себя в корне наоборот – он, как и квантовая частица в прямоугольной потенциальной яме, стремится быть поближе к центру ямы (к точке x = 0), и очень не любит подходить к стенкам (к точкам поворота). В возбуждённых состояниях по мере роста энергетического уровня у осциллятора постепенно появляется тяга к стенкам ямы. Это свидетельствует о том уже упоминавшемся факте, что с ростом энергии разница между результатами квантовой и классической механики становится всё меньше.
2). Квантовый осциллятор может быть обнаружен в классически недоступной области, и вероятность этого не так уж мала – даже на графиках видно, что в точках поворота значение функции распределения координат f (x) составляет примерно половину её максимального значения.
3). В возбуждённых состояниях у пси-функции появляются узлы. Это означает, что пси-поле частицы, находящейся в возбуждённых состояниях, делится на отдельные кванты, иначе говоря – расслаивается. Как уже отмечалось ранее, это – общая закономерность микромира, не зависящая от формы потенциальной ямы. Количество слоёв пси-поля (квантов) равно (n + 1), то есть снова совпадает, как и в случае прямоугольной потенциальной ямы с порядковым номером энергетического уровня.
[1] Термин «линейный осциллятор» означает то же самое, что и «одномерный осциллятор»,