Методы составления разностных схем

Лекция №9

Уравнения в частных производных

Введение

В физике, химии, биологии, социологии потребность в уравнениях в частных производных возникает при попытке описать динамику большого числа более или менее одинаковых дискретных объектов, входящих в некоторую системную целостность. Если количество таких дискретных объектом мало, то можно обойтись системой дифференциальных уравнений, в которой каждый дискретный объект описывается своей подсистемой обыкновенных дифференциальных уравнений.

В качестве примера можно привести модель хищник-жертва в математической биологии, когда хищник и жертва способны активно передвигаться, подобно тому, как передвигаются в водной среде планктонные организмы. Активное движение предполагает преследование хищником своей жертвы и, наоборот, убегание хищника от жертвы. В данном контексте оказалось возможным не только моделировать движение отдельных особей, но и описать динамику популяцию в целом. Поскольку количество планктона в океане это миллионы тонн, постольку описание предполагается в терминах плотностей биомасс отдельных видов. Следуя[1], можно привести следующие уравнения, описывающие динамику в пространстве и времени пары видов: одного вида хищника и одного вида жертвы:

(1)

где l ₁, l ₂ — параметры описывающие силы преследования и убегания, D ₁, D ₂ — коэффициенты диффузии, F₁, F₂ — члены ответственные за размножение жертвы, ее выедание хищником, и естественную смерть хищника.

Система уравнений (1) выведена из так называемого гидродинамического приближения, когда сообщество планктонных организмов рассматривается как сплошная среда. В качестве примера приведем уравнения, описывающие динамику вязкой несжимаемой жидкости:

(2)

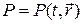где — поле скорости, — поле давления, r — плотность жидкости, m — кинематическая вязкость.

Наконец, приведем еще один пример уравнения теплопроводности, которое возникает в моделях сплошной среды для описания баланса тепла:

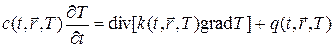, (3)

где — поле температуры, c — теплоемкость, k — коэффициент теплопроводности, q — плотность источников и стоков тепла.

К уравнениям в частных производных приводят задачи газовой динамики, гидродинамики, переноса излучения, теории упругости, описания электромагнитных полей, популяционной динамики, морфогенеза, математической экономики и во многих других задачах.

Из примеров (1) — (3) видно, что обычно в качестве независимых переменных выступает время t и пространство , но могут быть и другие независимые переменные. Обычно решение ищется в некоторой области изменения независимых переменных 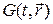. Для выделения единственного решения из некоторого семейства решений задают некоторые дополнительные условия, обычно формулируемые на границе области.

При изучении процессов во времени нас обычно интересуют решения на отрезке времени [ t ₀, t ₁], при этом область изменения независимых переменных может быть преобразована к виду:

. (4)

Согласно (4), решение определяется в области на отрезке времени [ t ₀, t ₁], причем дополнительное условие, заданное при t = t ₀ называется начальными данными, а на границе области — граничными или краевыми условиями.

Если в задаче определены только начальные данные, то ее называют задачей Коши. Так, для уравнения теплопроводности (3) в неограниченном пространстве можно сформулировать задачу с начальными данными

. (5)

Известно, что если 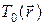— кусочно-непрерывная ограниченная функция, то решение задачи (3), (5) единственно в классе ограниченных функций.

Задачу с начальными и граничными условиями называют смешанной краевой задачей или нестационарной краевой задачей. Для смешаной задачи (3) дополнительные условия могут иметь, например, следующий вид:

. (6)

Часто постановка тех или иных физических задач приводит к ситуации, когда переходные процессы уже произошли и дальнейшая динамика отсутствует, т.е. зависимые переменные соответствующих уравнений не зависят от времени или являются стационарными. В этом случае задача формулируется в области , а дополнительные условия сводятся к краевым условиям на границе области .

Напомним известную классификацию уравнений в частных производных на примере одного уравнения, зависящего от двух переменных

. (7)

Если коэффициенты уравнения (7) не зависят от u, то уравнение является линейным, если коэффициенты являются константами — линейным уравнением с постоянными коэффициентами, если коэффициенты зависят от u, то уравнение (7) называется квазилинейным. Если A º B º C º 0. а D ¹ 0 и E ¹ 0, то уравнение (7) называется уравнением переноса и имеет первый порядок. Для уравнения второго порядка классификация определяется знаком дискриминанта B ² - AC. Для гиперболических уравнений дискриминант положителен, для параболических — равен нулю, для эллиптических уравнений — отрицателен.

Точные методы решения

В курсе уравнений математической физики[2] изложен ряд методов нахождения точных решений. К ним относятся метод распространения волн, метод разделения переменных, метод функции Грина или источника.

Например, для простейшей задачи теплопроводности:

(8)

методом разделения переменных можно найти точное решение в виде бесконечной суммы

(9)

где соответствующие коэффициенты Фурье от начальных данных находятся в соответствии с формулой

. (10)

Решение задачи (8) — (10) проиллюстрируем на конкретном примере, код программы для которого приведен на листинге_№1.

 

Листинг_№1

%Изображение аналитического решения уравнения

%теплопроводности, представленного в виде

%конечного отрезка бесконечного ряда

%очищаем рабочее пространство

clear all

%определяем коэффициент теплопроводности и

%длину отрезка интегрирования

k=1; a=1;

%определяем константы начального распределения

%температуры T0(x)=px, 0<=x<=0.5a; T0(x)=q(a-x),

%0.5a<x<=a

q=1; p=2;

%определяем число учтенных слагаемых

%бесконечного ряда

N=40;

%вычисляем первые N коэффициентов Фурье от

%начального распределения

for n=1:N

alpha(n)=((a*(q-p))/(pi*n))*cos(0.5*pi*n)+...

((2*a*(q+p))/(pi^2*n^2))*sin(0.5*pi*n);

end

%определяем сетки по времени и по пространству,

%в точках которых будет найдено значение температуры

t=0:0.05:10;

x=0:0.01:a;

%строим начальный температурный профиль T0

for j=1:length(x)

if x(j)<=0.5*a

T(j)=p*x(j);

end

if x(j)>0.5*a

T(j)=q*(a-x(j));

end

end

%рисуем начальный температурный профиль

plot(x,T,'Color','red','LineWidth',3);

hold on

%организуем цикл вычисления значений температуры

%в различные моменты времени и изображение их на

%едином графике

for i=1:length(t)

for j=1:length(x)

s=0;

for n=1:N

s=s+alpha(n)*...

exp(-(pi^2*n^2*k*t(i))/a^2)*...

sin((pi*n*x(j))/a);

end

T(j)=s;

end

plot(x,T);

hold on

end

 

На рис.1 приведен итог работы кода программы листинга_№1. Из графика видно, как начальные неоднородности, намеренно выбранные в виде острого кусочно-непрерывного профиля, со временем становятся гладкими линиями.

Подставляя (10) в (9) и меняя местами знаки интегрирование и суммирования, находим выражение для решения исходной задачи в терминах функции Грина

, (11)

где функция источника (Грина) равна

. (12)

 

Рис.1. Решение задачи (8) — (10)

 

Функция Грина для задачи Коши на всей оси имеет наиболее простой вид

. (12¢)

Функции влияния, подобные (12), (12¢) позволяют связать начальные данные с решением и сделать ряд важных замечаний о решениях в целом. Так, если начальное распределение сосредоточено на некотором отрезке [ a, b ], т.е. T ₀(x) > 0 при x Î [ a, b ] и T ₀(x) = 0, когда x Ï [ a, b ], то, согласно (11), (12¢), при t > 0 решение будет отличным от нуля в любой точке бесконечной оси. Это можно истолковать как то, что скорость распространения тепла в уравнении с линейной теплопроводностью бесконечна. Для сравнения с нелинейной теплопроводностью сошлемся на модель №5 в лекции №1. В этой модели рассматривалась ситуация остановки на некоторое время фронта тепловой волны.

Автомодельные решения

Уравнения в частных производных допускают классы упрощенных решений, которые получили название автомодельных. Для решений этого класса характерна зависимость функции решения от одной переменной x, которая является специальной комбинацией t, x.

Для построения примера автомодельного решения рассмотрим одномерное квазилинейное уравнение теплопроводности, в котором коэффициент теплопроводности степенным образом зависит от температуры, т.е.

, (13)

где k ₀, s — некоторые неотрицательные константы. Зависимости степенного типа, подобные (13), весьма распространены в физики. Так, в физике плазмы известно, что коэффициент электронной теплопроводности пропорционален .

Построим автомодельное решение для уравнения (13) типа бегущей волны:

. (14)

Подставляя (14) в (13), приходим к следующему обыкновенному дифференциальному уравнению:

. (15)

Уравнение (15) можно один раз проинтегрировать. Появится константа, которую определим, предполагая, что бегущая волна двигается по нулевому температурному фону. После этих предположений возможно провести еще одно интегрирование и в окончательном виде получить:

(16)

Возвращаясь в (16) к представлению в координатах t, x, получим

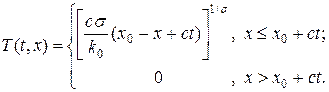(17)

Автомодельное решение (17) представляет собой температурную волну, бегущую с постоянной скоростью по нулевому температурному фону. Фронт волны имеет координату x ₀ + ct. Профили волны всюду гладкий, кроме фронта волны, где производная терпит разрыв.

На листинге_№2 приведен код программы, изображающей движение бегущей волны (17).

 

Листинг_№2

%Программа изображения бегущей волны квазилинейного

%уравнения теплопроводности

%очищаем рабочее пространство

clear all

%константы уравнения теплопроводности и бегущей волны

k0=1; sigma=3; c=4; x0=0.5;

%определяем сетки по времени и пространству

t=0:0.025:1;

x=0:0.01:5;

%организуем цикл рисования профиля температуры в

%различные моменты времени

for i=1:length(t)

%определяем профиль температуры

for j=1:length(x)

T(j)=0;

if x(j)<=x0+c*t(i)

T(j)=(((c*sigma)/k0)*(x0-x(j)+...

c*t(i)))^(1/sigma);

end

end

%рисуем температурный профиль

if i==1

plot(x,T,'Color','red','LineWidth',3);

else

plot(x,T);

end

hold on

end

 

На рис.2 приведены графики, изображающие движение бегущей температурной волны. Красным цветом выделен начальный температурный профиль.

 

Рис.2. Изображение бегущей волны (17)

 

Рассмотрим еще один пример автомодельного решения одномерного квазилинейного уравнения теплопроводности с источником:

. (18)

Уравнение (18) в отличие от (13) содержит источник тепла , степенным образом зависящий от температуры. Согласно исследованиям уравнения (18), проведенных в школе А.А. Самарского и С.П. Курдюмова[3], было установлено наличие так называемой “фундаментальной длины”, на которой происходит горение среды, при этом тепло не распространяется за пределы данной длины, а температура может расти неограниченно в течение конечного интервала времени. Уравнение (18) допускает специальный класс автомодельных решений, который получил название режимов с обострением.

Построим этот класс автомодельных решений. Для этого представим решение в виде:

. (19)

где t_f — время обострения или фокусировки.

Подставим (19) в (18), тогда

. (20)

Уравнение (20) допускает следующее аналитическое решение:

(21)

где 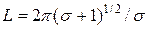— фундаментальная длина.

На листинге_№3 приведен код программы, изображающей режим с обострением (19), (21). Итоговый график вынесен на рис.3. Красным цветом на графике выделен начальный профиль.

 

Листинг_№3

%Программа изображения режима с обострением

%(19), (21)

%очищаем рабочее пространство

clear all

%определяем момент фокусировки и степень

%нелинейности sigma

tf=1; sigma=3;

%определяем фундаментальную длину

L=2*pi*sqrt(sigma+1)/sigma;

%задаем сетки по времени и по пространству

t=0.98:0.001:0.999;

x=-L:0.01:L;

%организуем цикл рисования профиля режима с

%обострением во времени

for i=1:length(t)

for j=1:length(x)

T(j)=0;

if abs(x(j))<0.5*L

T(j)=(tf-t(i))^(-1/sigma)*...

(((2*(sigma+1))/(sigma*(sigma+2)))*...

cos((pi*x(j))/L)^2)^(1/sigma);

end

end

%рисуем температурный профиль в начальный и в

%последующие моменты времени

if i==1

plot(x,T,'Color','red','LineWidth',3);

hold on

end

plo(x,T);

hold on

end

 

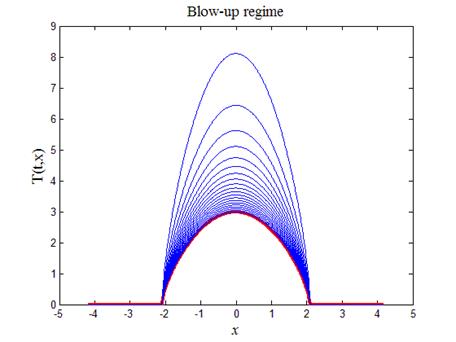
Рис.4. Режим с обострением (19), (21)

 

Разностный метод

Нелинейные уравнения в частных производных с коэффициентами достаточно общего вида, а также уравнения в областях достаточно общей формы обычно не удается решить аналитическими или автомодельными методами. Основным методом их решения являются численные методы, среди которых наиболее часто используемым является разностный метод.

Для использования разностного метода в области переменных 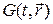вводят некоторую сетку. Все производные, входящие в уравнение, заменяют конечными разностями значений функций в узлах сетки. Полученное в результате алгебраическое уравнение называют разностной схемой. Решая алгебраическую систему уравнений, находят приближенные (разностные) значения функции в узлах сетки. Возникают обычные вопросы при постановке вычислительного эксперимента:

· Существует ли решение алгебраической системы уравнений и является ли оно единственным?

· Каков эффективный алгоритм поиска решения?

· При каких условиях численное решение сходится к точному решению и с какой скоростью?

Есть еще пара вопросов, которые ранее в нашем практикуме не возникали. Это процедура выбора сетки и составление разностной схемы на этой сетке. Для иллюстрации последних двух вопросов рассмотрим пример.

Составим пару простейших разностных схем для линейного одномерного уравнения теплопроводности в ограниченной области G.

, (22)

. (23)

Решение уравнения теплопроводности (22) с начальными и граничными условиями (23) ищется в ограниченной области G = [0 £ x £ a ] ´ [0 £ t £ T ].

Введем в области G сетку, образованные пересечением прямых линий x_n = nh, n = 0,1,…, N и t_m = mt, m = 0,1,…, M. Считаем для простоты сетку равномерной по оси x и t соответственно. Величины h и t являются шагами сетки по переменным x и t соответственно (рис.5,а). Значения функции в узлах сетки представим в виде: .

 

Рис.5,а. Разностная схема для задачи (22), (23)	Рис.5,б. Шаблон разностной схемы (24), (25)	Рис.5,в. Шаблон разностной схемы (26)

 

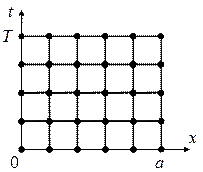
В начале построим разностную схему для численного решения уравнения (22) следуя конфигурации узлов на рис.5,б. В уравнении (22) заменим производную u_t на разностное отношение , а вторую производную u_xx — 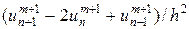. В результате можно получить разностную схему следующего вида

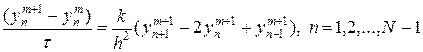(24)

для приближенного решения уравнения (22). Недостающие уравнения для решения задачи (24) берутся из начальных и граничных условий (23), т.е.

. (25)

Конфигурация узлов (рис.5,б) лежащая в основе разностной схемы (24), (25) называется шаблоном.

Для одной и той же задачи можно составить множество разностных схем. Например, если в качестве шаблона разностной схемы выбрать шаблон на рис.5,в, то

. (26)

Начальные и граничные значения для разностной схемы (26) можно записать по аналогии с (25).

В дальнейшем будут рассмотрены различные способы составления и исследования разностных схем для различных типов уравнений. В дальнейших лекциях будут изложены те разностные схемы, которые хорошо себя зарекомендовали при решении тех уравнений математической физики, которые используются в задачах переноса, теплопроводности, диффузии, акустики, газодинамики, электричества и в ряде других областях.

Для большинства разностных схем узлы сетки лежат обычно на пересечении некоторых прямых линий (гиперповерхностей в многомерных задачах). Для двумерных задач в прямоугольной области наиболее часто используют прямоугольную сетку (см., например, рис.5,а). Заметно реже используют треугольную сетку (рис.6,а). Для трехмерных задача наиболее употребительна сетка из прямоугольных параллелепипедов (рис.6,б). На рис.6,в приведен пример менее употребительной трехмерной сетки, состоящей из трехгранных призм.

 

Рис.6,а. Пример треугольной сетки	Рис.6,б. Пример трехмерной сетки	Рис.6,в. Пример трехмерной сетки

 

Если одной из переменных в задаче является время t, тогда совокупность узлов сетки, на линии (гиперплоскости) t = t_m называют слоем. Узлы разностной схемы связанные друг с другом согласно шаблону называются регулярными, остальные узлы — нерегулярными. Нерегулярными обычно являются граничные узлы. Например, на рис.7,а приведен пример двумерной прямоугольной сетки, на которой построена сложная область с криволинейной границей. Жирным крестом внутри области обозначены регулярные узлы разностной схемы связанные с помощью шаблона, представленного на рис.7,б. Звездами обозначены некоторые нерегулярные узлы в окрестности криволинейной границы области.

 

Рис.7,а. Пример сложной области и прямоугольной сетки	Рис.7,б. Шаблон разностной сетки

 

Вернемся к разностной схеме (26). Положим в этой схеме m = 0, т.к. известно из начального условия, можно найти при n = 1,…, N -1. Значения и находим из граничных условий (25). Тем самым значения функции на первом временной слое найдены. Аналогичная процедура может быть проделана при определении и т.д. Схема, похожая на (26), т.е. такая схема, в которой значение функции на следующем слое легко выразить через значения функции на текущем слое называется явной.

Схема (24) на следующем временном слое содержит в каждом уравнении несколько неизвестных значений. Подобные схемы называют неявными. Перепишем схему (24) и граничные условия (25) в следующем виде:

(27)

На каждом слое схема (27) представляет собой систему линейных уравнений для определения неизвестных величин . Матрица данной алгебраической системы уравнений трехдиагональная и решение может быть найдено с помощью обычной алгебраической прогонки.

Невязка

Рассмотрим операторное уравнение общего вида

Au = f или в иной форме Au - f = 0. (28)

Заменим оператор A разностным оператором A_h, правую часть f — некоторой сеточной функцией j_h, а точное решение u — разностным решением y, тогда можно записать разностное схему вида:

A_hy = j_h или в другой форме A_hy - j_h = 0. (29)

Если в (29) подставить точное решение u, то оно, вообще говоря, не будет удовлетворять уравнению, т.е. A_hu ¹ j_h. Величину

y = j_h - A_hu = (Au - f) - (A_hu - j_h) = (Au - A_hu) - (f - j_h).

принято называть невязкой. Для ее оценки обычно используют разложение в ряд Тейлора.

Найдем невязку для явной разностной схемы (26). Перепишем исходное уравнение теплопроводности (22) в форме (28)

.

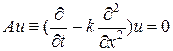Поскольку f = j_h = 0, постольку

(30)

где .

Разложим решение u по формуле Тейлора в окрестности узла (t_m, x_n), считая что по времени существует вторая непрерывная производная, а по пространству — четвертая непрерывная производная, тогда

(31)

где , , 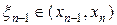. Подставляя (31) в (30) и пренебрегая отличием величин 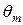, и от t_m и x_n, находим итоговую оценку невязки

. (32)

Согласно (32), невязка стремится к нулю при t ® 0 и h ® 0. Оценка (32) дает оценку невязки в регулярных узлах сетки. Согласно (23), (25), граничные условия выполняются точно, т.е. .

Оценку невязки (32) можно улучшить следующим образом. Найдем u_tt согласно следующей последовательности выкладок

. (33)

Подставляя (33) в (32), получим

. (34)

Согласно формуле (34) можно положить, что , тогда главный член невязки (34) обратиться в нуль и останутся члены более высокого порядка малости. Такой прием используется для получения разностных схем повышенного порядка точности.

Методы составления разностных схем

Различают три метода построения разностных схем на заданном шаблоне:

· метод разностной аппроксимации;

· интегро-интерполяционный метод;

· метод неопределенных коэффициентов.

Методом разностной аппроксимации мы уже пользовались при составлении схем (24), (26). Согласно данному методу, каждая производная, входящая в уравнение и краевое условие, заменяется каким-либо разностным выражением с учетов узлов заданного шаблона. Метод позволяет легко составить разностные схемы с первым и вторым порядком аппроксимации, когда коэффициенты уравнения достаточно гладкие функции. Обобщение данного подхода на ряд важных случаев затруднителен. Например, если коэффициенты уравнения разрывные, или предполагается использовать непрямоугольную и неравномерную сетку, возникает неопределенность в построении разностной схемы.

При использовании интегро-интерполяционного метода или метода баланса используют дополнительные физические соображения, сводящиеся к составлению уравнений сохранения тех или иных величин. В данном методе после выбора шаблона область 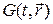разбивается на ячейки. Дифференциальное уравнение интегрируют по ячейке и по формулам векторного анализа приводят к интегральной форме, отвечающей некоторому интегральному закону. Интегралы вычисляют приближенно по одной из квадратурных формул и получают разностную схему.

Представим уравнение теплопроводности с переменным коэффициентом теплопроводности в виде: . Выберем для его аппроксимации шаблон, представленный на рис.8, где пунктиром выделена соответствующая ячейка.

Выполним интегрирование по ячейке:

и аппроксимируем первый интеграл по формуле средних, а второй интеграл — по формуле прямоугольников, тогда

.

В последнем выражении производные заменим конечными разностями и, считая сетку равномерной, получим разностную схему

. (35)

Если k = const, то схема (35) совпадает с неявной схемой (24).

 

Рис.8. Шаблон и ячейка интегро-интерполяционного
метода для уравнения теплопроводности

 

Интегро-интерполяционный метод наиболее полезен, когда коэффициенты уравнения является негладкими или даже разрывными. В этом случае обращение к более общим — интегральным законам возвращает нас к более правильным обобщенным решениям.

Рассмотрим пример использования разностной схемы (35) для расчета теплопроводности среды, состоящей из трех сред с разными коэффициентами теплопроводности, т.е.

(36)

где k ₁, k ₂, k ₃, вообще говоря, различные неотрицательные числа. Исходное уравнение можно в этом случае записать в виде:

(37)

Для расчета по схеме (35) с коэффициентом теплопроводности (36) будем полагать, что

, (38)

а на левой x = 0 и правой x = a границе согласно (37) будем поддерживать нуль температуры, т.е. и .

На листинге_№4 приведен код программы, которая решает уравнение (36), (37) согласно разностной схеме (35), (38).

 

Листинг_№4

%Программа решения уравнения теплопроводности

%(37) с разрывным коэффициентом

%теплопроводности (36)

function ktmp

global a k1 k2 k3

%определяем отрезок интегрирования и

%три значения коэффициента теплопроводности

%в трех областях отрезка интегрирования

a=3; k1=0.1; k2=100; k3=10;

%определяем шаг по времени и по пространству

tau=0.05; h=0.05;

x=0:h:a; N=length(x);

%Строим начальное распределение температуры

Tm=7;

for i=1:N

if x(i)<=0.5*a

y(i)=((2*Tm)/a)*x(i);

end

if x(i)>0.5*a

y(i)=((2*Tm)/a)*(a-x(i));

end

end

%рисуем начальный профиль температуры

%толстой красной линией

plot(x,y,'Color','red','LineWidth',3);

hold on

%вычисляем коэффициенты прогонки A(n), B(n)

%C(n): A(n)y2(n+1)+B(n)y2(n)+C(n)y2(n-1)=y(n)

for t=1:20

for n=2:(N-1)

A(n)=-(tau/h^2)*k(x(n)+0.5*h);

B(n)=1+(tau/h^2)*...

(k(x(n)+0.5*h)+k(x(n)-0.5*h));

C(n)=-(tau/h^2)*k(x(n)-0.5*h);

end

%определяем левое граничное условие

alpha(2)=0; beta(2)=0;

for n=2:(N-1)

alpha(n+1)=-A(n)/(B(n)+C(n)*alpha(n));

beta(n+1)=(y(n)-C(n)*beta(n))/...

(B(n)+C(n)*alpha(n));

end

%задаем правое граничное условие

y(N)=0;

for n=(N-1):-1:1

y(n)=alpha(n+1)*y(n+1)+beta(n+1);

end

%рисуем текущий профиль температуры

plot(x,y);

hold on

end

%определяем коэффициент теплопроводности

function z=k(x)

global a k1 k2 k3

if (x>=0)&(x<=a/3)

z=k1;

end

if (x>a/3)&(x<=(2*a)/3)

z=k2;

end

if (x>(2*a)/3)&(x<=a)

z=k3;

end

 

На рис.9 приведен итог работы кода программы листинга_№4. Красной жирной линией нарисован начальный треугольный профиль температуры. Вертикальные стрелки на графике отделяют области с разными коэффициентами теплопроводности. Согласно коду листинга_№4, коэффициенты теплопроводности отличаются друг от друга на три порядка.

 

Рис.9. Решение уравнения теплопроводности (37) с разрывным
коэффициентом теплопроводности (36)

 

Метод неопределенных коэффициентов заключается в том, что в качестве разностной схемы берут линейную комбинацию решений в узлах некоторого шаблона. Коэффициенты линейной комбинации определяют из условия максимального порядка соответствующей невязки по t и h.

Так, для уравнения на шаблоне рис.8 можем записать следующую схему с неопределенными коэффициентами

. (39)

Определяем невязку

. (40)

Подставим (31) в (40), тогда

(41)

Большинство членов в (41) обнуляются при условии

,

т.е. при

. (42)

Подставляя (42) в (39) получим разностную схему (24).

Метод неопределенных коэффициентов применим и к более сложным случаям. Например, для треугольной сетки, шаблон которой приведен на рис.10 можно получить следующую разностную схему

. (43)

 

Рис.10. Шаблон треугольной сетки для разностного уравнения (43)

 

Рассмотрим нерегулярные узлы разностной схемы, т.е. ее граничные условия. Для уравнения теплопроводности u_t = k u_xx нерегулярными являются граничные узлы n = 0 и n = N. Если рассматривается первая краевая задача

,

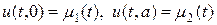то легко записать соответствующие разностные условия

,

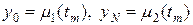которые выполняются точно, т.к. невязка для них равна нулю.

Более сложным является случай второй краевой задачи, когда граничное условие содержит производную по x. Например, при задании на краях теплового потока граничные условия приобретают следующий вид:

. (44)

Производные в (44) можно аппроксимировать правой (левой) конечной разностью:

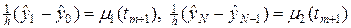. (45)

Невязка разностных уравнений (45) легко оценивается:

(46)

Таким образом, согласно (46), невязка граничных условий имеет первый порядок точности по h, тогда как в регулярных точках порядок точности второй по h, т.е. при выборе аппроксимации граничных условий по формулам (45) происходит потеря точности.

Для повышения точности граничных условий рассмотрим метод фиктивных точек. Введем вне отрезка [0, a ] две фиктивные точки: 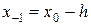, и запишем в точках n = 0 и n = N явную разностную схему (26), тогда

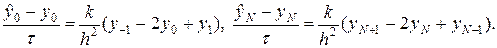(47)

Аппроксимируем левое и правое граничное условие с помощью центральной разности, т.е.

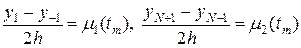. (48)

Исключая из (47), (48) фиктивные точки и значения функции в них, находим граничные условия второго порядка точности по h:

(49)

Граничные условия (49) являются явными, т.к. содержат только по одному значению на следующем слое.

Помимо метода фиктивных точек есть другой метод уменьшения невязки, он более универсален, но менее нагляден. Разложим u (t, x ₁) в окрестности x ₀, тогда

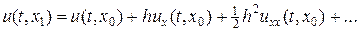
Согласно (44), , а из уравнения теплопроводности найдем . Подставляя данные оценки в разложение Тейлора, находим

(50)

Делая в (50) замену , получим левое граничное условие (49).

Согласно приведенной выше процедуре можно добиться повышенной точности в аппроксимации граничных условий.

Аппроксимация

Пусть задана область G переменных x = (x ₁, x ₂,…, x_p) с границей G и поставлена корректная задача решения уравнения с граничными условиями:

Au (x) - f (x) = 0, x Î G; (51)

Ru (x) - m (x) = 0, x Î G. (52)

Введем в области G + G сетку с шагом h, которая содержит регулярные (внутренние) узлы w_h и нерегулярные (граничные) узлы g_h.

Перейдем в (51), (52) к соответствующим разностным аналогам

A_hy_h (x) - j_h (x) = 0, x Î w_h; (51¢)

R_hy_h (x) - c_h (x) = 0, x Î g_h. (52¢)

Близость разностной схемы (51¢), (52¢) к исходной задаче (51), (52) определяется величинами невязок:

;

.

Разностная схема (51¢), (52¢) аппроксимирует задачу (51), (52), когда

,

аппроксимация имеет p -й порядок, когда

.

Дадим некоторые комментарии к выбору норм. Для простоты будем рассматривать одномерный случай, т.е. G = [ a, b ].

Можно использовать чебышевскую или локальную норму

,

или гильбертову, среднеквадратическую:

.

Часто строят ассоциированные или связанные с оператором A энергетические нормы. Например,

.

Выбор нормы регулируется двумя противоположными соображениями. С одной стороны, желательно, чтобы разностное решение y было близко к точному решению в наиболее сильной© норме. Например, в задачах на разрушение конструкций малость деформаций в не гарантирует целостность конструкций, а малость в норме — гарантирует. С другой стороны, чем слабее норма , тем легче разностную схему построить и доказать ее сходимость.

Функции y_h, j_h, c_h, входящие в (51¢), (52¢), определены на сетке, поэтому д