Лабораторная работа 2
Алгоритмы Прима и Крускала
Маршрутом в графе называется последовательность вершин и ребер, которая обладает следующими свойствами:
1. она начинается и заканчивается вершиной;
2. вершины и ребра в ней чередуются;
3. любое ребро последовательности имеет своими концами две вершины: непосредственно предшествующую ему в этой последовательности, и следующую сразу за ним. Первая и последняя вершины в этой последовательности называются началом и концом маршрут
Путем называется такой маршрут, в котором никакое ребро не встречается дважды. Иногда его также называют цепью
Связный граф – если любая вершина достижима из любой другой вершины. В противном случае – несвязный. Несвязный граф распадается на несколько частей, каждая из которых является связным графом. Эти части называются компонентами связности.
Граф называется связным, если для любых двух его вершин v, w существует простая цепь из v в w.
Граф (орграф) называется связным (сильно связным), если для любых двух его вершин v, w существует маршрут (путь), соединяющий v, w (из v и w).
Орграф называется односторонне связным, если для любых его двух вершин, по крайней мере, одна достижима из другой.
Если граф не является связным, то он называется несвязным.
Любой несвязный граф состоит из нескольких связных графов, каждый из которых называется компонентой связности графа. В частности у связного графа ровно одна компонента связности.
Компонентой связности графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа.
В дальнейшем количество компонент связности графа будем обозначать k.
Циклическое ребро – если оно входит хотя бы в один цикл графа. В противном случае – ациклическое.
Эйлеровым путем в графе называется путь, содержащий все ребра графа. Эйлеровым циклом в графе называется цикл, содержащий все ребра графа.
Деревья
Неориентированное дерево (или просто дерево) – это конечный связный граф с выделенной вершиной (корнем) без циклов. Дерево не имеет петель и кратных рёбер. Дерево и названо деревом, поскольку, будучи нарисованным, выглядит как дерево, только перевёрнутое «вверх ногами».
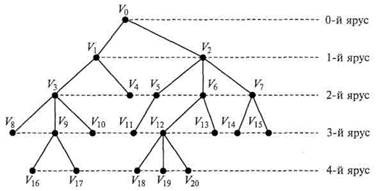
Рисунок 1 – Граф является деревом
Граф, изображённый на рисунке 1, является примером дерева. Граф на рисунке 2 не является деревом, поскольку содержит цикл.
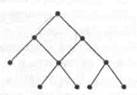
Рисунок 2 – Граф деревом не является
Понятие дерева широко используется во многих областях математики и информатике. Например, они используются как инструмент при вычислениях, как удобный способ хранения данных, способ сортировки или поиска данных.
Наиболее характерные свойства деревьев, которые одновременно служат эквивалентными определениями дерева, можно сформулировать в следующей теореме.
Теорема. Граф G(V,E) (ǀ V ǀ= n>1) является деревом тогда и только тогда, когда выполняется хотя бы одно из условий:
граф G(V,E) связан и не содержит циклов;
граф G(V,E) не содержит циклов и имеет n-1 ребро;
граф G(V,E) связан и имеет n-1 ребро;
граф G(V,E) не содержит циклов, но добавление ребра между несмежными вершинами приводит к появлению одного и только одного элементарного цикла;
граф G(V,E) связный, но утрачивает это свойство после удаления любого ребра;
в графе G(V,E) всякая пара вершин соединена цепью, и только одной.
Итак, дерево с n вершинами имеет n-1 ребро, поэтому оно будет минимальным связным графом.
Лес – это граф, компоненты которого являются деревьями.
Граф на рисунке 3 – это лес.
Рисунок 3 – Лес
Подграф исходного графа G(V,E), являющийся деревом и содержащий все его вершины, называется остовом. Остовное дерево графа состоит из минимального подмножества рёбер графа, таких, что из одной из вершин графа можно попасть в любую другую вершину, двигаясь по этим рёбрам.
Минимальным остовным деревом (МОД) связного взвешенного графа называется его связный подграф, состоящий из всех вершин исходного дерева и некоторых его ребер, причем сумма весов ребер минимально возможная. Если исходный граф не связан, то описываемую ниже процедуру можно применять поочередно к каждой его компоненте связности, получая тем самым минимальные остовные деревья для этих компонент.
МОД для связного графа можно найти простым перебором. Поскольку множество ребер МОД является подмножеством в множестве ребер исходного графа, можно просто перебрать все возможные подмножества и найти среди них МОД. Нетрудно видеть, что это чрезвычайно трудоемкий процесс. В множестве из N ребер имеется 2N подмножеств. Для каждого из этих подмножеств мы должны будем проверить, что оно задает связный подграф, охватывающий все вершины исходного, и не содержит циклов, а затем сосчитать его вес. Процесс можно ускорить после того, как найдено первое остовное дерево. Никакое подмножество ребер, полный вес которого больше, чем у уже найденного наилучшего остовного дерева, не может нам подойти, поэтому нет необходимости проверять связность, ацикличность и охват всех вершин.
Жадные алгоритмы
В жадном алгоритме(greedy algorithm) всегда делается выбор, который кажется самым лучшим в данный момент, т.е. производится локально оптимальный выбор в надежде, что он приведет к оптимальному решению глобальной задачи. Жадный подход строит решение посредством последовательности шагов, на каждом из которых получается частичное решение поставленной задачи, пока не будет получено полное решение. При этом на каждом шаге, и это является главным в рассматриваемом методе, выбор должен быть
· допустимым, т.е. удовлетворять ограничениям задачи;
· локально оптимальным, т.е. наилучшим локальным выбором среди всех допустимых вариантов, доступных на каждом шаге;
· окончательным, т.е., будучи сделан, он не может быть изменен последующими шагами алгоритма.
Эти требования поясняют название метода: на каждом шаге он предполагает «жадный» выбор наилучшей доступной альтернативы в надежде, что последовательность локально оптимальных выборов приведет к глобально оптимальному решению всей задачи. Существуют задачи, для которых последовательность локально оптимальных выборов приводит к оптимальному решению для любого экземпляра рассматриваемой задачи, но есть и другие задачи, для которых это не так; для задач такого рода жадный алгоритм может представлять интерес только в том случае, если нас устраивает приближенное решение.
Алгоритм Крускала
Алгоритм Крускала – алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Алгоритм впервые описан Джозефом Крускалом в 1956 году.
Формулировка задачи
Дан взвешенный граф, в котором веса присвоены ребрам. Необходимо найти минимальное остовное дерево имеющую своим корнем одну из вершин графа.
Алгоритм
1. Текущее множество рёбер устанавливается пустым.
2. Далее, пока это возможно, проводится следующая операция: из всех рёбер, добавление которых к уже имеющемуся множеству не вызовет появление в нём цикла, выбирается ребро минимального веса и добавляется к уже имеющемуся множеству.
3. Когда таких рёбер больше нет, алгоритм завершён.
4. Подграф данного графа, содержащий все его вершины и найденное множество рёбер, является его остовным деревом минимального веса.
Пример 1
Дан исходный граф
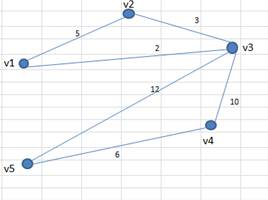
Построить для заданного графа минимальное остовное дерево
Решение
1. Разместим все ребра графа в порядке их возрастания
2. Выбираем ребро V1V3, строим его
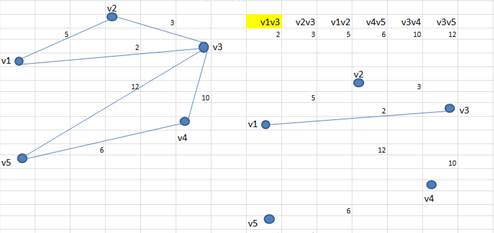
3. Выбираем ребро V2V3, данное ребро безопасно (не образует цикла) присоединяем его к дереву
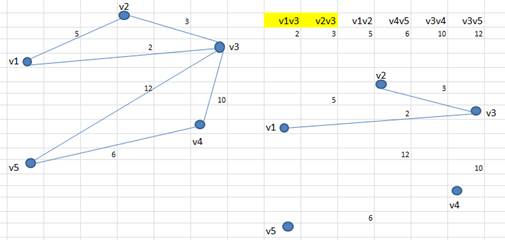
4. Выбираем ребро V1V2, данное ребро образует цикл, поэтому присоединять его к дереву нельзя
5. Выбираем ребро V4V5, данное ребро безопасно (не образует цикла) присоединяем его к дереву
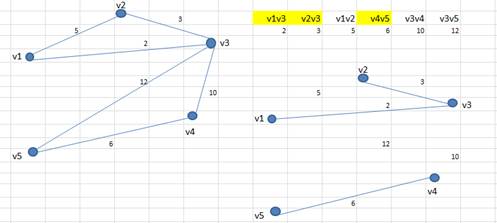
6. Выбираем ребро V3V4, данное ребро безопасно (не образует цикла) присоединяем его к дереву
7. Выбираем ребро V3V4, данное ребро безопасно (не образует цикла) присоединяем его к дереву
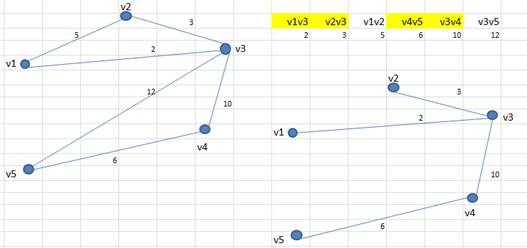
8. Выбираем ребро V3V5, данное ребро образует цикла, поэтому присоединять его к дереву нельзя. (Но данное действие уже является избыточным, т.к. все вершины графа уже соединены ребрами)
9. Минимальное остовное дерево построено
Однако, данный пример позволяет отследить наличие/отсутствие циклов только визуально, что не возможно при программной реализации. Рассмотрим подход, позволяющий отслеживать безопасные ребра, при отсутствии визуальной картинки. Буде использовать понятие компоненты связности.
Пример 2
1. Рассмотрим решение на основе данных из Примера 1. Нам потребуется список ребер по возрастанию их весов и список вершин графа
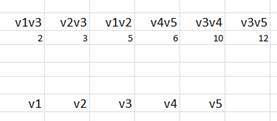
2. Выбираем первое ребро V1V3, оно принадлежит первой компоненте связности, помечаем вершины, инцидентные данному ребру одним цветом (можно пометить цифрой 1). И помечаем данное ребро, как присоединенное к дереву.
3. Выбираем следующее ребро V2V3, оно принадлежит второй компоненте связности, помечаем вершины, инцидентные данному ребру одним цветом (можно пометить цифрой 2).
Но вершина V3 уже связана с вершиной V1, поэтому помечаем все три вершины одним цветом, все они принадлежат теперь одной компоненте связности. И помечаем данное ребро, как присоединенное к дереву.
4. Выбираем следующее ребро V1V2, и видим, что обе вершины, инцидентные данному ребру, принадлежат одной и той же компоненте связности. Следовательно, образуется цикл и данное ребро не является безопасным.
5. Выбираем следующее ребро V4V5, оно принадлежит третьей компоненте связности, помечаем вершины, инцидентные данному ребру одним цветом (можно пометить цифрой 3). И помечаем данное ребро, как присоединенное к дереву.
6. Выбираем следующее ребро V3V4, видим, что вершины принадлежат разным компонентам связности, поэтому их можно присоединить к дереву. Помечаем вершины, инцидентные данному ребру одним цветом (можно пометить цифрой 4).
Но обе эти вершины связаны с вершинами компонент связности 2 и 3. Поэтому объединяем эти компоненты в одну общую. И помечаем данное ребро, как присоединенное к дереву.
Все вершины исходного графа включены в дерево и связаны, следовательно, минимальное остовное дерево построено, оно включает в себя все помеченные ребра.
Алгоритм Прима
Алгоритм Прима обладает тем свойством, что ребра в множестве А всегда образуют единое дерево.
Дерево начинается с произвольной корневой вершины V и растет до тех пор, пока не охватит все вершины.
На каждом шаге к дереву А добавляется легкое ребро, соединяющее дерево и отдельную вершину из оставшейся части графа. Причем, добавляются только безопасные для дерева А ребра; т.е. ребра минимального веса, добавление которых к уже имеющемуся множеству не вызовет появления в нём цикла.
Таким образом, по завершении алгоритма ребра в А образуют минимальное остовное дерево.
Данная стратегия является жадной, поскольку на каждом шаге к дереву добавляется ребро, которое вносит минимально возможный вклад в общий вес.
Пример
Дан исходный граф.
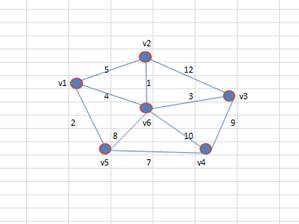
Найти минимальное остовное дерево
Решение:
1. Построим матрицу весовых коффициентов (матрицу весов)
2. Вершиной – стоком может быть любая из вершин, выберем вершину V1. Оостовное дерево не должно содержать циклов. Помечаем столбец V1, как пройденный, и строку V1 – рабочую область на данном шаге.
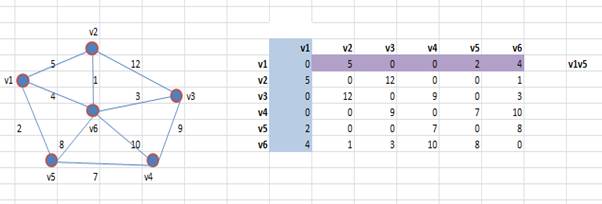
Выбираем минимальный элемент из рабочей области, если таких элементов два, выбираем тот, который стоит левее. Это элемент (ребро) весом 2.
Выписываем вершины, соединяемые этим ребром. Это вершины V1V5
3. Помечаем столбец V5, как пройденный, и строку V5. В рабочую область теперь входят две строки.
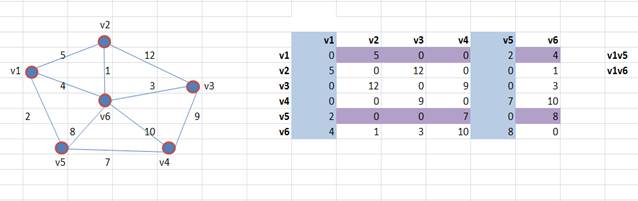
Выбираем минимальный элемент из рабочей области. Это элемент (ребро) весом 4.
Выписываем вершины, соединяемые этим ребром. Это вершины V1V6
4. Помечаем столбец V6, как пройденный, и строку V6. В рабочую область теперь входят три строки.
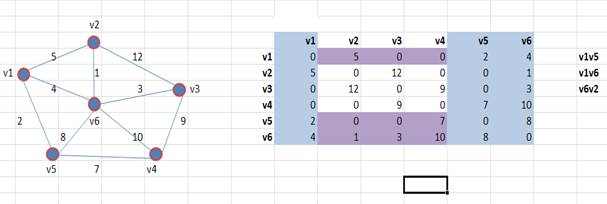
Выбираем минимальный элемент из рабочей области. Это элемент (ребро) весом 1.
Выписываем вершины, соединяемые этим ребром. Это вершины V6V2
5. Помечаем столбец V2, как пройденный, и строку V2. В рабочую область теперь входят четыре строки.
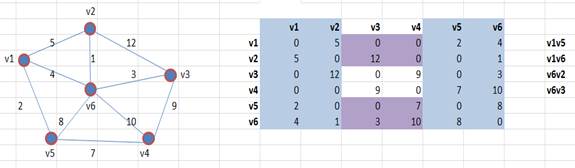
Выбираем минимальный элемент из рабочей области. Это элемент (ребро) весом 3.
Выписываем вершины, соединяемые этим ребром. Это вершины V6V3
6. Помечаем столбец V3, как пройденный, и строку V3. В рабочую область теперь входят пять строк.
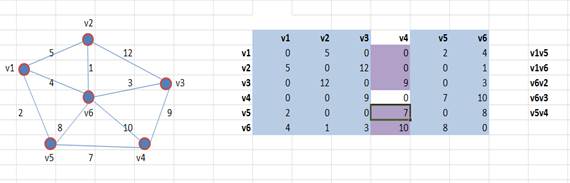
Выбираем минимальный элемент из рабочей области. Это элемент (ребро) весом 7.
Выписываем вершины, соединяемые этим ребром. Это вершины V5V4
7. Помечаем столбец V4, как пройденный. Все вершины помечены. Строим минимальное остовное дерево
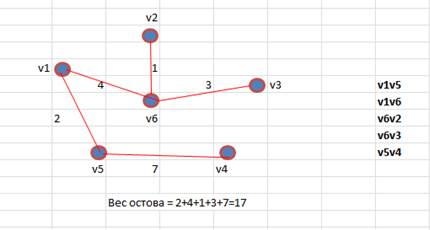
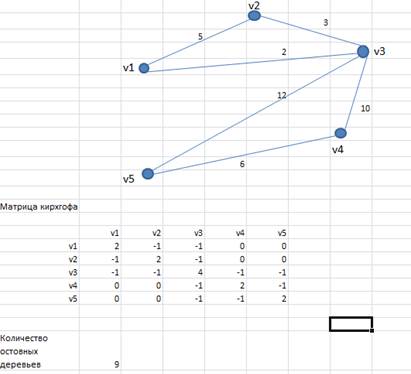
Для подсчета общего количества остовов в рассматриваемом графе используется матрица Кирхгофа
Матрица Кирхгофа
Если в матрице смежности графа G, заменить каждый элемент на противоположный, а на диагонали вместо элемента Aij поставить степень вершины i (если имеются кратные рёбра, то в степени вершины они учитываются со своей кратностью). Тогда, согласно матричной теореме Кирхгофа, все алгебраические дополнения этой матрицы равны между собой, и равны количеству остовных деревьев этого графа. Например, можно удалить последнюю строку и последний столбец этой матрицы, и модуль её определителя будет равен искомому количеству.
Матричная теорема Кирхгофа
Теорема. [Кирхгоф Г.]. Число остовных деревьев в связном графе G (V,E) порядка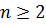 
равно алгебраическому дополнению любого диагонального элемента матрицы Кирхгофа 
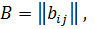где
Пример
Найти количество остовных деревьев для графа, изображенного на рисунке 4
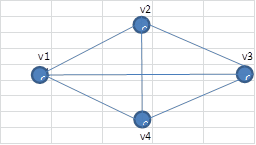
Рисунок 4 – Исходный граф
Матрица Кирхгофа этого графа имеет вид:
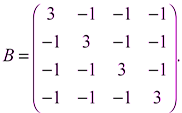
Минор любого диагонального элемента этой матрицы равен
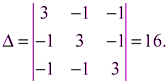
Следовательно, данный граф имеет 16 остовных деревьев.
Следствие. Число остовов в полном графе Kn равно nn-2
Задания для самостоятельного решения
1. С помощью алгоритмов Крускала и Прима построить и рассчитать минимальное остовное дерево для графа и вычислить общее количество остовных деревьев
2. С помощью алгоритмов Крускала и Прима построить и рассчитать минимальное остовное дерево для графа и вычислить общее количество остовных деревьев
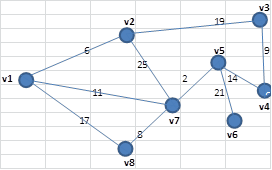
Индивидуальное задание
1.. С помощью алгоритмов Крускала и Прима построить и рассчитать минимальное остовное дерево для графа и вычислить общее количество остовных деревьев для графов, соответствующих номерам вашим заданиям из ЛР1.