УКРАИНСКИЙ МОРСКОЙ ИНСТИТУТ

Ю.М. Рудов
ИНТЕГРАЛ
(Таблицы – Формулы - Задачи)

Севастополь, 2010
ББК 22.151.5+22.143
УДК 519. 2 (076.1)
Рудов Ю.М. – доктор технических наук, профессор
Интегралы. Методические указания по изучению учебной дисциплины «Высшая математика», раздел «Интегральное исчисление » для студентов I курса дневной и заочной формы обучения инженерных и экономических специальностей.- Севастополь: УМИ, 2010.– 12 с.
Рецензент:
Методические указания утверждены на заседании кафедры естественно-научных дисциплин УМИ
Протокол №3 от
Рекомендовано к печати учебно-методическим советом УМИ
Протокол №1
Оглавление
1. Неопределенный интеграл. Определение, свойства, таблица, два метода интегрирования.  4
4
1.1 Неопределенный интеграл. 4
1.1.1. Свойства: 4
1.2. Таблица интегралов. 4
1.3. Методы интегрирования. 5
1.3.1 Метод замены переменного. 5
1.3.2. Метод интегрирования по частям.. 5
2. Определенный интеграл. Определение, формулы, задачи с решениями. 6
2.1. Вычисление площадей плоских фигур. 6
2.1.1.Декартовые координаты.. 6
2.1.2.Параметрические координаты.. 7
2.1.3. Уравнение циклоиды в параметрических координатах. 7
2.1.4.Полярные координаты.. 7
2.2. Вычисление длин дуг. 8
2.2.1.Параметрические координаты.. 9
2.3. Вычисление объемов. 11
2.3.1.Вычисление объема тора. 12
ФОРМУЛЫИ ТИПИЧНЫЕ ЗАДАЧИ НА ИНТЕГРАЛЫ
1. Неопределенный интеграл. Определение, свойства, таблица, два метода интегрирования. 

 1.1 Неопределенный интеграл.
1.1 Неопределенный интеграл.

Здесь F (x) – первообразная функция. Правильность вычисления интеграла проверяется следующим образом: если продифференцировать ответ, то должна получится подинтегральная функция.
1.1.1. Свойства:
1. 
2. 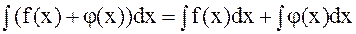
3. 
4. 
Таблица интегралов
1. 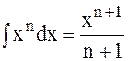 ,
,  1а.
1а.  1б.
1б. 
2. 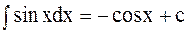 3.
3. 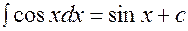
4. 
5. 
6.  7.
7. 
8.  9.
9. 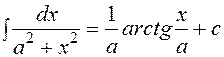
10. 
11.  12.
12. 
13. 
В правых частях формул 1б, 4, 5, 6, 13 содержится функция  - это натуральный логарифм, в основании которого число
- это натуральный логарифм, в основании которого число  , часто используемое во многих фундаментальных дисциплинах
, часто используемое во многих фундаментальных дисциплинах 
Методы интегрирования
Метод замены переменного
 , замена
, замена  ,
, 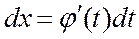

Пример: Вычислить 
Решение: Введем замену  , тогда
, тогда 
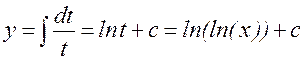
Метод интегрирования по частям
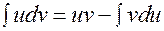
Пример: Вычислить 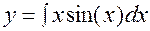
Решение: 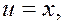

 ,
, 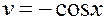 ;
;

Определенный интеграл. Определение, формулы, задачи с решениями
.
 2.1. Вычисление площадей плоских фигур
2.1. Вычисление площадей плоских фигур
Декартовые координаты
Вычислить площадь фигуры, ограниченной линиями:
Для решения задачи применим формулу вычисления площади криволинейной трапеции
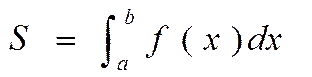

Если криволинейная трапеция ограничена двумя кривыми линиями, то формула имеет вид:


Решение


Параметрические координаты
 | |||||
 | |||||
 | |||||
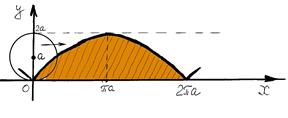
Пример: Вычислить площадь фигуры, ограниченной осью ОХ и одной аркой циклоиды.
Линия циклоиды образуется следующим образом. Закрепим карандаш в точке О окружности и начнем «катить» окружность без скольжения по оси ОХ. Тогда карандаш изобразит указанную кривую. Один оборот окружности образует первую арку циклоиды, следующий оборот – вторую арку и так далее.
Уравнение циклоиды в параметрических координатах



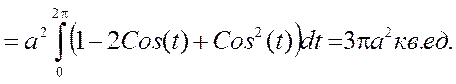
Полярные координаты
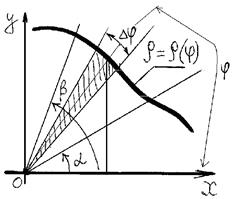

Площадь кругового сектора Площадь криволинейного сектора

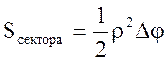

Пример: Вычислить площадь фигуры, ограниченной лемнискатой

| 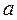
| |
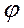
| 
|


Решение: В силу симметрии фигуры вычислим четвертую часть площади, а затем результат увеличим в 4 раза:
 |
Вычисление длин дуг
Декартовые координаты. Для вывода формулы, пользуемся теоремой Пифагора и определением производной функции:
 |

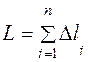
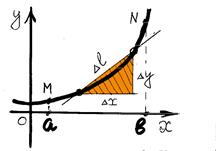
Пример: Определить длину окружности радиуса r
Уравнение окружности:



Решение: Для упрощения вычислений сначала определим длину четвертой части окружности, а затем результат увеличим в четыре раза
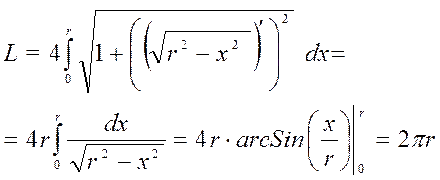 |
Здесь для вычисления интеграла воспользовались табличной формулой 12.
Параметрические координаты


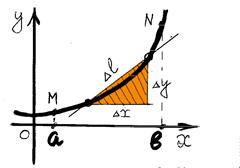
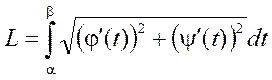
(*)
Пример: Вычислить длину дуги одной арки циклоиды.
Способ построения циклоиды был указан на странице 6. Линию называют также брахистохроной. По такой форме на Востоке строят крыши зданий, так как именно циклоида обеспечивает быстрейшее «скатывание» дождевой воды.
Решение: Уравнение циклоиды
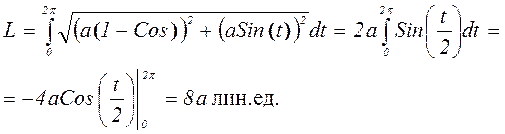
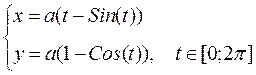

Полярные координаты
Из ∆ 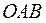 запишем связь декартовых и
запишем связь декартовых и
полярных координат

Воспользуемся формулой (*) предыдущего пункта, правилом дифференцирования произведения функций и основным тригонометрическим тождеством:
 | |||
 | |||
В приведенных преобразованиях мы применили правило дифференцирования произведения двух функций:
 ,
,
А также дважды использовали основное тригонометрическое тождество:

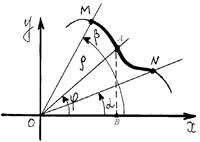
Пример: Найти длину кардиоиды. Дадим понятие кардиоиды. Расположим две окружности (каждая диаметром  ) как показано на рисунке: окружности внешне касаются, их центры расположены на оси OX. Если в точке М правой окружности закрепить мел и начать ее «катить» без скольжения по неподвижной левой окружности, то мел изобразит сердцевидную кривую, которая и называется кардиоидой.
) как показано на рисунке: окружности внешне касаются, их центры расположены на оси OX. Если в точке М правой окружности закрепить мел и начать ее «катить» без скольжения по неподвижной левой окружности, то мел изобразит сердцевидную кривую, которая и называется кардиоидой.
Уравнение кардиоиды в полярных координатах
имеет вид:


Решение: Для облегчения вычислений воспользуемся симметрией линии, а затем результат удвоим:
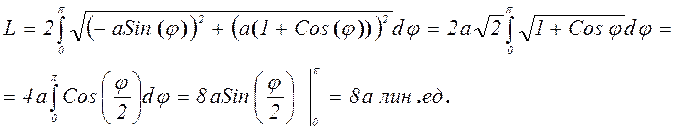
Вычисление объемов
Объем тела вращения вокруг оси ОХ. Объем прямого кругового цилиндра

Плоская фигура вращается вокруг оси ОХ
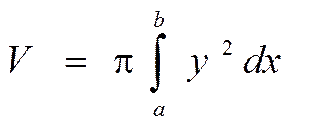
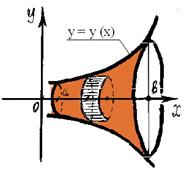
Пример: Вычислить объем тела, полученного от вращения кривой у = 2х вокруг оси ОХ, если 
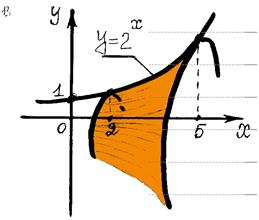
Решение:

Здесь воспользовались формулой Ньютона-Лейбница для вычисления определенного интеграла:
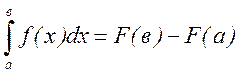
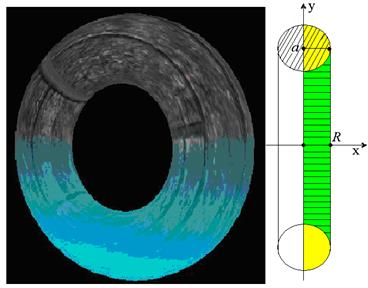
Вычисление объема тора
Тор – это объемное тело, получаемое от вращения круга радиуса R относительно оси ОХ (см.рисунок). Примерами тора может служить бублик или накаченная камера автомобиля.
Уравнение окружности со смещенным центром на 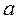
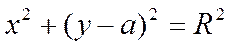 |
единиц по оси У имеет вид
 |
или в явной форме
 |
В нашем примере пределы по х от - R до + R.