Теория массового обслуживания – раздел прикладной математики, который изучает свойства систем массового обслуживания (СМО) с целью повышения эффективности их работы.
Система массового обслуживания – это совокупность взаимосвязанных объектов (приборов), предназначенная для обслуживания заявок (требований), поступающих в систему в случайные моменты времени. При этом не только моменты поступления заявок в систему, но и длительность обслуживания каждой заявки представляют собой случайные величины.
Наиболее распространенными примерами таких систем являются билетные кассы, системы связи, АЗС, сервисные центры, ремонтные мастерские, аудиторские фирмы, телефонные станции, банки, службы скорой помощи и такси, компьютерные сети и т. д.
Условно СМО можно изобразить в виде следующей схемы.
Входящий поток – это поток требований, поступающих в систему, а выходящий поток – покидающих систему.
Входящий поток называют простейшим, если выполняются следующие три свойства:
– в каждый момент времени в систему не может поступить более одной заявки,
– вероятность числа заявок, поступающих за данный промежуток времени, зависит только от длины этого промежутка и не зависит от места его расположения на оси времени,
– вероятность числа заявок, поступающих в систему за данный промежуток времени, не зависит от числа заявок поступивших в нее в предыдущие промежутки времени.
Состоянием СМО в данный момент называют общее число требований (заявок), находящихся в системе в этот момент. Тогда система может иметь следующие состояния:
– 
– в системе нет заявок,
– 
– в системе 1 заявка,
– 
– в системе 2 заявки, и т. д.
Таким образом, символ 
обозначает событие, состоящее в том, что в системе в момент 
есть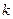 
заявок. Пусть 
– вероятность того, что в момент система находится в состоянии .
Про систему говорят, что она функционирует в стационарном режиме, если вероятность 
ее пребывания в состоянии 
есть величина, зависящая только от числа 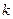и не зависящая от момента рассмотрения функционирования системы и длительности нахождения системы в состоянии .
Рассмотрим систему, которая функционирует в стационарном режиме, имеет простейший поток со средней интенсивностью, равной 
(интенсивность потока – это среднее число заявок, поступающих в систему в единицу времени). Пусть в системе имеется один прибор, который в единицу времени в среднем обслуживает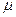 
заявок ( 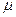–средняя производительность прибора).
Если нет никаких дополнительных ограничений на длину очереди (или количество заявок в системе), то система называется системой без потерь (без ограничений) и в ней может находиться любое число заявок. Оказывается, что для такой системы имеют место следующие формулы: 
, (6)
и 
. (7)
Поясним, как получается значение для 
. Поскольку СМО является системой без ограничений, то случайная величина принимает бесконечно много значений, и следовательно, имеется бесконечно много значений вероятностей , сумма которых равна 1: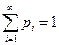 
. В силу формулы для вычисления , будем иметь
.
Отсюда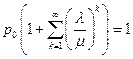 
, и так как сумма 
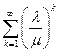является суммой бесконечно убывающей геометрической прогрессии с первым членом 
и таким же знаменателем, то находится из уравнения 
, и .
Отношение обозначают символом 
и называют коэффициентом использования системы. С введением этого коэффициента, вероятности и можно вычислять по формулам 
; 
.
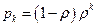
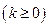Используя указанные формулы, легко составить закон распределения случайной величины и найти основные характеристики системы.
Рассмотрим конкретную задачу.
Задача 22. Пусть СМО функционирует в стационарном режиме, имеет один прибор со средней производительностью 
, при этом поток заявок, поступающих на обслуживание, считается пуассоновским, а его средняя интенсивность 
заявкам в минуту. Требуется определить:
а) вероятность того, что в очереди будет более двух заявок. б) вероятность того, что в очереди ровно 
заявок;
в) вероятность того, что заявке не придется ждать своего обслуживания.
Решение. а) В очереди больше двух заявок тогда, когда в системе больше трех заявок (в этом случае наименьшее число заявок в системе образуется из двух заявок в очереди и одной заявки на приборе). Следовательно, искомая вероятность равна суме вероятностей возможных состояний системы, начиная с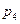 
: 
.
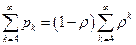Так как для функционирования (без “затоваривания”) системы необходимо условие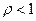 
, то сумма 
является суммой бесконечно убывающей геометрической прогрессии с первым членом 
и знаменателем . Тогда 
, и так как 
, то 
.
б) В очередировно заявок тогда, когда в системе находятся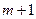 
заявка. Вероятность такого события 
.
в) Заявке не придется ждать в том случае, когда система пуста – в ней нет ни одной заявки. Следовательно, ответом является вероятность : 
.
23. Пусть система функционирует в режиме задачи 22, причем 
. Найдите вероятность того, что а) в очереди будет не более двух заявок; в) в очереди будет ровно 3 заявки; с) заявке не придется ждать.
Рассмотрим теперь СМО, которая функционирует в том же режиме, что и в предыдущих задачах, но с ограничениями (с потерями). Пусть число заявок в очереди не может быть более двух. Это означает, что в системе не может находиться более трех заявок, и каждая четвертая заявка, приходящая в систему, получает отказ (теряется). В этом случае для вычисления вероятностей событий при 
также применяется формула (6), но вероятность находится иначе. В этом случае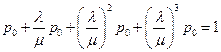 
, и следовательно, 
, где 
–сумма четырех членов геометрической прогрессии, у которой первый член равен 1, а знаменатель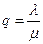 
.
Задача 24. Пусть СМО функционирует в стационарном режиме, имеет один прибор со средней производительностью , при этом поток заявок, поступающих на обслуживание, считается пуассоновским, и его средняя интенсивность заявкам в минуту. Также предполагается, что очередь на обслуживание не может превышать двух заявок. Требуется определить:
а) вероятность того, что приходящая заявка получит отказ;
б) среднее число заявок в очереди;
в) среднее время ожидания.
Решение. Так как в очереди не может быть более двух заявок, то самое большее число заявок в системе – 3 (это число равно числу приборов + максимальное число заявок в очереди). Согласно основному свойству стационарного режима работы СМО,
, и
.
Отсюда найдем, что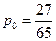 
. Теперь можно составить закон распределения случайной величины 
:
|
| ||||
|
| 
| 
| 
| 
|
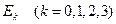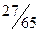
а) Приходящая заявка получит отказ, если в системе 3 заявки, то есть если прибор занят и 2 заявки в очереди. Таким образом, вероятность этого события равна 
.
б) Среднее число заявок в очереди равно математическому ожиданию случайной величины: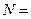 
.
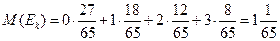в) Среднее время пребывания заявки в системе вычисляется по формуле Литтла: 
. В нашей задаче 
(мин.).