Урок - лекция
Тема урока: Применение определенного интеграла для нахождения площади криволинейной трапеции. Формула Ньютона—Лейбница.
Цели: познакомить с определённым интегралом, его вычислением по формуле Ньютона – Лейбница и применением для нахождения площади криволинейной трапеции.
Задание: изучить материал урока, выписать формулу Ньютона-Лейбница, законспектировать все примеры урока, выполнить домашнее задание.
ХОД УРОКА
Математическая разминка
Для функции найдите первообразную.
| f(x) | F(x) |
| x | |
| |
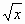
| 2x | |
| Sin 2x |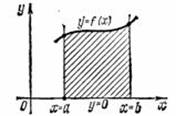 
|
2. Изучение нового материала
Сегодня мы рассмотрим применение первообразной, и интеграла к вычислению площадей плоских фигур. Рассмотрим фигуру, которую назовём криволинейной трапецией.
Определение: Криволинейной трапецией назовём фигуру, ограниченную осью х, прямыми х = а, х = b (а < b) и графиком непрерывной и неотрицательной на отрезке [а;b] функции у=f(x).
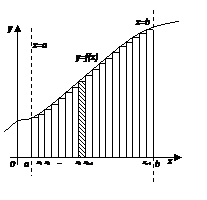Найдем, используя геометрические соображения, приближенное значение площади криволинейной трапеции. Для этого разобьем отрезок [а;b] (основание криволинейной трапеции) на n равных частей с помощью точек 
, …, 
, 
,…, 
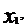
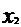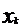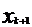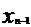. Проведем соответствующие ординаты. Криволинейная трапеция разбилась на n частей – на n узеньких столбиков. Площадь трапеции будет равна сумме площадей столбиков.
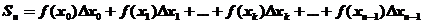
Считаем, что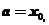 
, 
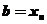. Приближенное равенство 
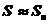тем точнее, чем больше n. Принято считать, что искомая площадь криволинейной трапеции равна пределу последовательности (
): 
.
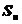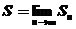В курсе математического анализа доказано, что этот предел существует. Его называют определенным интегралом от функции у=f(х) по отрезку [а; b] и обозначают так: 
; читают: интеграл от а до b эф от икс дэ икс. Числа а и b называют пределами интегрирования (соответственно нижним и верхним).
S=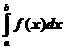 
; здесь S – площадь криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла.
Масса неоднородного стержня с плотностью p(x) вычисляется по формуле m=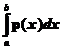 
. В этом состоит физический смысл определенного интеграла.
Перемещение s точки, движущейся по прямой со скоростью v(t), за промежуток времени от t=а до t=b, вычисляется по формуле s=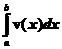 
. Это еще одно физическое истолкование определенного интеграла.
А как вычислить определённый интеграл?
В курсе математического анализа доказана следующая теорема.
Теорема. Если функция y= f(x) непрерывна на отрезке [а; b], то справедлива формула
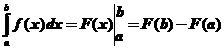, где F(x) – первообразная для f(x).
Приведенную формулу называют формулой Ньютона – Лейбница.
Основные свойства определенного интеграла:
1. При перестановке пределов интегрирования изменяется знак интеграла:
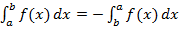
2. Отрезок интегрирования можно разбивать на части:
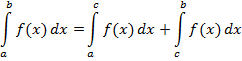
3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов.
4. Постоянный множитель можно выносить за знак интеграла.
Пример 1. Вычислить определенный интеграл
= 
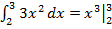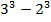=27-8=19.
Пример 2. Вычислить определенный интеграл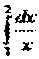 
.
Решение:
= 
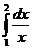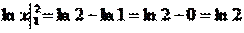
Пример 3. Вычислить определенный интеграл: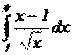 
.
Решение:
.
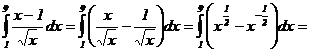
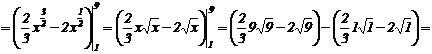
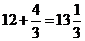Используя определённый интеграл можно находить площади плоских фигур.
Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.
Для нахождения суммарной площади используется формула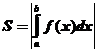 
.
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
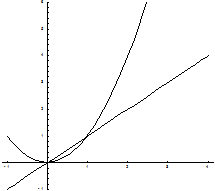Пример 1 Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
 |
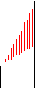Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
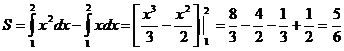(ед2)
Пример 2
Вычислить площадь фигуры, ограниченной линиями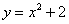 
, 
, 
, 
.
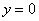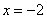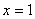Выполним чертеж (обратите внимание, что уравнение 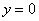задает ось 
):
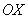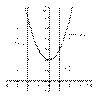
На отрезке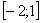 
график функции 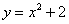расположен над осью 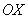, поэтому:
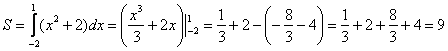
Ответ: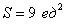 
Пример 3
Вычислить площадь фигуры, ограниченной линиями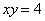 
, 
, 
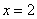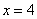и осью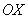
Это пример для самостоятельного решения.
Пример 2: Решение:
Выполним чертеж: 
На отрезке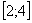 
график функции 
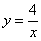расположен над осью 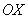, поэтому:
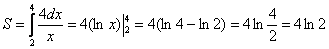
Ответ: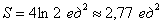 
Пример 4
Вычислить площадь фигуры, ограниченной линиями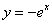 
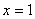, и координатными осями.
Решение: Выполним чертеж:
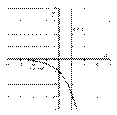
Если криволинейная трапеция полностью расположена под осью 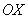, то её площадь можно найти по формуле: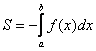 
В данном случае:
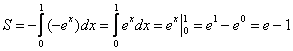
Ответ: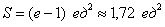 
Пример 5
Найти площадь плоской фигуры, ограниченной линиями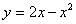 
, 
.
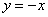Решение: Сначала нужно выполнить чертеж. Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы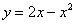 
и прямой 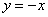. Это можно сделать двумя способами. Первый способ – аналитический. Решаем уравнение:
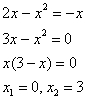
Значит, нижний предел интегрирования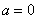 
, верхний предел интегрирования 
.
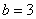Этим способом лучше, по возможности, не пользоваться.
Гораздо выгоднее и быстрее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».
Выполним чертеж:
Искомая фигура ограничена параболой 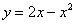сверху и прямой 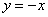снизу.
На отрезке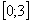 
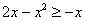, по соответствующей формуле:
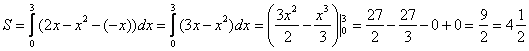
Ответ: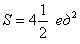 
Домашнее задание: § 56,57, 58, № 1014