Лекция 4. Прямая линия на плоскости.
Вопросы:
1. Понятие уравнения линии в R2.
2. Уравнение прямой с угловым коэффициентом.
3. Угол между прямыми.
4. Условия параллельности и перпендикулярности прямых.
5. Уравнение прямой, проходящей через две точки.
6. Общее уравнение прямой.
7. Расстояние от точки до прямой.
8. Решение экономических примеров.
Уравнение линии на плоскости
Определение 2.9. Уравнением линии (кривой) на плоскости Оxy называется уравнение, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
В общем виде уравнение линии может быть записано виде 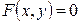 (или если это возможно)
(или если это возможно)  , где
, где 
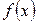 — некоторые функции.
— некоторые функции.
Если точка  передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты точки
передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты точки  называются текущими координатами. Буквы, входящие в уравнение называются параметрами.
называются текущими координатами. Буквы, входящие в уравнение называются параметрами.
Точка пересечения двух линий, заданных уравнениями  и
и 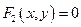 находится решением системы
находится решением системы 
Надо отметить, что не каждое уравнение определяет линию на плоскости. Например,  определят точку
определят точку 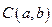 ;
;  не определят никакой линии;
не определят никакой линии;  определят две линии
определят две линии  .
.
Чтобы составить уравнение линии заданной некоторым свойством нужно:
1) взять произвольную (текущую) точку 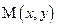 линии;
линии;
2) записать равенством общее свойство всех точек М линии;
3) входящие в это равенство отрезки (и углы) выразить через текущие координаты точки 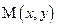 и через данные задачи.
и через данные задачи.
Пример 2.4. Вывести уравнение линии, для точек которой кратчайшее расстояние до данной окружности  и прямой
и прямой 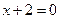 равны между собой.
равны между собой.
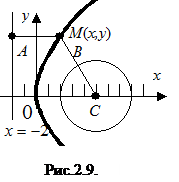 Решение. Окружность имеет центр в точке
Решение. Окружность имеет центр в точке 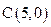 и радиус
и радиус  Возьмем текущую точку
Возьмем текущую точку 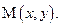 По условию АМ = ВМ. Найдем эти отрезки и упростим полученное равенство. Так как координаты
По условию АМ = ВМ. Найдем эти отрезки и упростим полученное равенство. Так как координаты 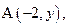 то
то 
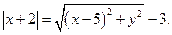 Из чертежа видно, что
Из чертежа видно, что 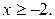 Поэтому
Поэтому  или
или 
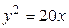 — парабола (см. рис.2.9).
— парабола (см. рис.2.9).
Уравнение прямой, проходящей через две данные точки
Уравнение прямой, проходящей через две точки М 1 (x 1; у 1) и М 2 (x 2, y 2), записывается в виде
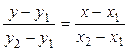 (2.7)
(2.7)
Доказательство. Возьмем текущую точку М (x; у) на прямой, проходящей через точки М 1(x 1; у 1) и М 2(x 2,y2). Из условия коллинеарности векторов  , получаем
, получаем  , что и требовалось доказать.
, что и требовалось доказать.
Пример 2.5. Составить уравнение прямой, проходящей через точки
М (-1,3) и N (2,5).
Решение. Полагая  ,
,  ,
, 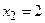 ,
, 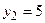 в уравнении (2.7) получаем
в уравнении (2.7) получаем
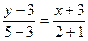 , или
, или 
Итак, искомое уравнение имеет вид 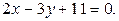
Полезно проверить, что уравнение составлено верно. Для этого достаточно показать, что координаты точек М и N удовлетворяют уравнению прямой. Действительно, равенство  выполняется тождественно.
выполняется тождественно.
Уравнение прямой в отрезках
 Уравнение прямой по заданным отрезкам
Уравнение прямой по заданным отрезкам 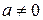 и
и  отсекаемым на осях координат, т. е. уравнение прямой проходящей через точки
отсекаемым на осях координат, т. е. уравнение прямой проходящей через точки  и
и  имеет вид
имеет вид
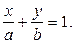 (2.8)
(2.8)
Доказать самостоятельно.
Рис. 2.10
2.2.4. Уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору (по нормальному вектору и точке)
Пусть прямая проходит через точку  , перпендикулярно вектору
, перпендикулярно вектору 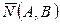 (Рис. 2.11).
(Рис. 2.11).
 Так как
Так как 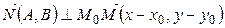 , то из условия перпендикулярности векторов имеем
, то из условия перпендикулярности векторов имеем
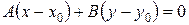 . (1.9)
. (1.9)
Раскрывая скобки, получаем 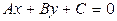 , где
, где 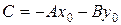 .
.
Рис. 2.11
Отсюда следует, что если задано уравнение прямой 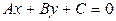 , то вектор
, то вектор  будет перпендикулярным до этой прямой. Он называется нормальным вектором прямой. Этот факт широко используется при решении различных задач.
будет перпендикулярным до этой прямой. Он называется нормальным вектором прямой. Этот факт широко используется при решении различных задач.
Общее уравнение прямой
Теорема. Всякое уравнение первой степени относительно x и y, т.е. уравнение вида
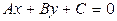 , (2.10)
, (2.10)
где А, В и С — постоянные коэффициенты, причем  , определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.
, определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.
Доказательство. Возьмем произвольную точку 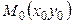 на линии
на линии 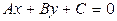 , то есть должно выполнятся равенство
, то есть должно выполнятся равенство 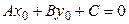 . Отсюда
. Отсюда  Следовательно, исходное уравнение равносильно уравнению
Следовательно, исходное уравнение равносильно уравнению 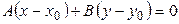 , а это, согласно предыдущему пункту, — уравнение прямой.
, а это, согласно предыдущему пункту, — уравнение прямой.
Проведем исследование общего уравнения прямой 
1. 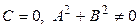 , то есть уравнение
, то есть уравнение  Эта прямая проходит через начало координат.
Эта прямая проходит через начало координат.
2.  , то есть уравнение
, то есть уравнение  Эта прямая параллельна оси Ох поскольку она перпендикулярна вектору
Эта прямая параллельна оси Ох поскольку она перпендикулярна вектору  , который перпендикулярный оси Ох.
, который перпендикулярный оси Ох.

 , то есть уравнение
, то есть уравнение 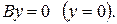 Эта прямая совпадает с осью Ох.
Эта прямая совпадает с осью Ох.
3. 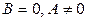 , то есть уравнение
, то есть уравнение  Эта прямая параллельна оси Оy поскольку она перпендикулярна вектору
Эта прямая параллельна оси Оy поскольку она перпендикулярна вектору 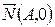 , который перпендикулярный оси Оy.
, который перпендикулярный оси Оy.

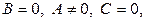 то есть уравнение
то есть уравнение  Эта прямая совпадает с осью Оy.
Эта прямая совпадает с осью Оy.
Уравнение пучка прямых
Определение 2.10. Угловым коэффициентом прямой называется тангенс угла наклона прямой к оси Ох.
Угловой коэффициент этой прямой, проходящей через две точки (Рис. 2.12) находится по формуле
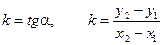 ,
, 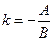 (2.11)
(2.11)

Рис. 2.12
Уравнение (7) можно записать в виде 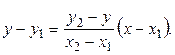 Учитывая значение углового коэффициента k, получаем уравнение пучка прямых, проходящих через точку
Учитывая значение углового коэффициента k, получаем уравнение пучка прямых, проходящих через точку  (Рис. 2.13):
(Рис. 2.13):
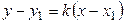 (2.12)
(2.12)

Рис. 2.13
В таком виде нельзя записать уравнение вертикальной прямой. Если 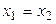 , то уравнение прямой, проходящей через точки М 1 и М 2 имеет вид
, то уравнение прямой, проходящей через точки М 1 и М 2 имеет вид
 . (2.13)
. (2.13)
Если  то уравнение прямой, проходящей через точки M 1 и М 2 имеет вид
то уравнение прямой, проходящей через точки M 1 и М 2 имеет вид
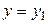 . (2.14)
. (2.14)