Если вероятность  появления случайного события
появления случайного события 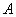 в каждом испытании постоянна, то вероятность
в каждом испытании постоянна, то вероятность 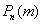 того, что в
того, что в  испытаниях событие
испытаниях событие 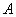 наступит ровно
наступит ровно 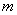 раз, приближённо равна:
раз, приближённо равна:
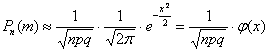 , где
, где  .
.
При этом, чем больше  , тем рассчитанная вероятность
, тем рассчитанная вероятность 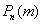 будет лучше приближать точное значению
будет лучше приближать точное значению 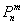 , полученное (хотя бы гипотетически) по формуле Бернулли. Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат
, полученное (хотя бы гипотетически) по формуле Бернулли. Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат 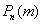 может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность
может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность  ближе к 0,5, и наоборот – даёт существенную погрешность при значениях
ближе к 0,5, и наоборот – даёт существенную погрешность при значениях  , близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы
, близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы  является выполнение неравенства
является выполнение неравенства 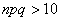 (
(  ).
).
Так, например, если  , то
, то  и применение теоремы Лапласа для 50-ти испытаний оправдано. Но если
и применение теоремы Лапласа для 50-ти испытаний оправдано. Но если  и
и 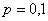 , то
, то  и приближение
и приближение 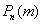 (к точному значению
(к точному значению 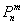 ) будет плохим.
) будет плохим.
Биномиальное распределение, его математическое ожидание, дисперсия
Рассмотрим серию независимых  испытаний проведенных в условиях схемы Бернулли, в ходе которых появлялось событие
испытаний проведенных в условиях схемы Бернулли, в ходе которых появлялось событие 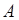 с вероятностью
с вероятностью  , одинаковой для всех испытаний.
, одинаковой для всех испытаний.
Необходимо определить закон распределения случайной величины 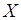 числа появлений события
числа появлений события 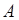 . Для этого нужно определить возможные значения
. Для этого нужно определить возможные значения 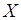 и их вероятности. Минимальное значение
и их вероятности. Минимальное значение 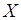 равно нулю, что соответствует ситуации, когда в серии
равно нулю, что соответствует ситуации, когда в серии  испытаний событие
испытаний событие 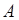 не появилось; максимальное значение
не появилось; максимальное значение 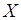 соответствует «успеху» во всех испытаниях серии и равно
соответствует «успеху» во всех испытаниях серии и равно  . Очевидно, что случайная величина
. Очевидно, что случайная величина 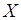 числа появлений события
числа появлений события 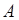 в серии
в серии  испытаний принимает значения
испытаний принимает значения  . Остается найти соответствующие вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:
. Остается найти соответствующие вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:
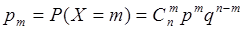 ,
,
где 
 ,
, 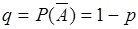 .
.
Эта формула является аналитическим выражением искомого закона распределения. Эта формула еще называется биномиальной, так как ее правая часть представляет собой 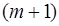 -й член бинома Ньютона:
-й член бинома Ньютона:
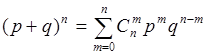 .
.
Отсюда сразу видно, что для полученного закона биномиального распределения вероятностей числа появления события 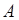 при
при  независимых испытаниях выполняется условие нормировки, т.е. сумма всех вероятностей равна единице:
независимых испытаниях выполняется условие нормировки, т.е. сумма всех вероятностей равна единице:
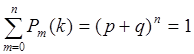 .
.
Теорема. Математическое ожидание числа появлений события 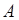 в
в  независимых испытаниях равно произведению числа испытаний на вероятность появления события
независимых испытаниях равно произведению числа испытаний на вероятность появления события 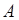 в каждом испытании.
в каждом испытании.
Доказательство. Случайная величина 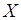 распределена по биномиальному закону:
распределена по биномиальному закону:
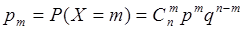 (
(
 ),
),
где 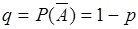 .
.
Величину 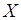 можно рассматривать, как сумму независимых случайных величин
можно рассматривать, как сумму независимых случайных величин  , где
, где 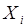 (
(
 ) – число появлений события
) – число появлений события 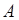 в
в 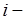 м испытании. Случайная величина
м испытании. Случайная величина 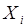 принимает лишь два значения: 1, если событие
принимает лишь два значения: 1, если событие 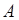 появилось в
появилось в 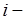 м испытании, и 0, если в
м испытании, и 0, если в 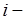 м испытании события
м испытании события 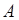 не произошло.
не произошло.
Вероятности этих событий  и
и  , а математическое ожидание:
, а математическое ожидание:  (
(
 ).
).
Следовательно, используя теорему о математическом ожидании суммы, получим:
 .
.
Таким образом, математическое ожидание числа появлений события 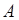 в условиях схемы Бернулли совпадает со средним числом появлений события
в условиях схемы Бернулли совпадает со средним числом появлений события 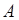 в данной серии испытаний.
в данной серии испытаний.
Дисперсия числа появлений события 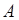 в
в  независимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления события
независимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления события 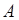 в одном испытании:
в одном испытании: 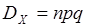 .
.