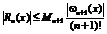Билет N 9
Интерполяционные многочлены Ньютона. Оценка погрешности.
Пусть дана табличная функция f(x) с постоянным шагом h. Значение функции задано в n+1 узле интерполирования. В силу теоремы о существовании и единстве интерполяционного многочлена для данной функции с n+1 узлом интерполирования существует единственный интерполяционный многочлен n-ой степени Pn(x) такой, что выполняется условие
Pn(xi)=yi (i=1,…,n)(1)
Представим этот многочлен в следующем виде:
(2) Pn(x)=a0+a1(x-x0)+a2(x-x0)(x-x1)+
+…+ an(x-x0)(x-x1)… (x-xn)
Неизвестны a0,a1,a2,…,an –коэффициенты
Эти коэффициенты нужно определить.
Воспользуемся условием (1), т.е. из условия, что в узлах интерполирования значение многочлена и значение табличной функции равны.
Возьмем х=х0, получим
Pn(x0)=а0=y0 а0=y0
X=x1: Pn(x1)=a0+a1(x-x0)
y1-y0=a1h Þ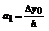 
X=x2:Pn(x1)=a0+a1(x-x0)+a2(x-x0)(x-x1)
в общем виде: 
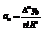
Данная формула называется первым интерполяционным многочленом Ньютона.
На практике эта формула применяется в несколько другом виде:
Возьмем 
, тогда
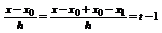
и формула (3) перепишется:
Если заменить функцию f(x)»Pn(x)-первым интерполяционным многочленом Ньютона, то получим первую интерполяционную формулу Ньютона.
Первый интерполяционный многочлен Ньютона используется для интерполирования в начале таблицы, т.е. дает большую точность для х»х0.
Для интерполирования в конце таблицы, т.е. для вычислений х»хn используется второй интерполяционный многочлен Ньютона.
Найдем его.
(4)Pn(x)=a0+a1(x-xn)+a2(x-xn)(x-xn-1)+…+an(x-xn)* *(x-xn-1)… (x-x1)
Коэффициенты находятся из условия совпадения интерполяционного многочлена с табличной функцией в узлах интерполирования.
х=хn; a0=yn;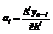 
тогда
возьмем 
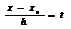, тогда
(6)
Если задать функцию f(x) на второй итерационной последовательности, то получим вторую интерполяционную формулу Ньютона. f(x)»Pn(x) (7)
Погрешность интерполирования по формулам Ньютона.
Погрешность определяется по формуле: Rn(x)=f(x)-Pn(x)
Имеет место следующее соотношение: (8)
- для первого интерполяционного многочлена Ньютона
Данные формулы для оценки погрешностей можно применять если известно аналитическое выражение интерполяционной функции, и если функция f(x) имеет производные до n+1 порядка включительно
Однако при малых h мы можем взять
здесь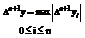 
Поэтому формулы (8) и (9) можно переписать в следующем виде:
Интерполяционный многочлен Лагранжа. Оценка погрешности.
Пусть дана табличная функция y=f(x), заданная в (n+1) узле интерполирования.
| X | X0 | X1 | … | Xn |
| Y=f(x) | Y0 | Y1 | … | yn |
Построим интерполяционный многочлен n-й степени для которого выполняется условие:
Ln(xi) = yi, i=0, 1, … n (1)
Будем искать многочлен Ln(x) в следующем виде: (2) Ln(x)=l1(x)+l2(x)+…+ln(x)
Здесь li(x) – многочлен степени n такой, что: (3) 
Условия (2) и (3) обеспечивают выполнение условия (1). Многочлены li(x) строятся следующим образом:
(4) li(x)=ci*(x-x0)*(x-x1)*…*(x - xi-1)*(x – xi+1)*…*(x – xn)
Здесь ci – постоянный коэффициент, значение которого можно определить из условия (3) т.е.
Если подставить значение ci в (4) то получим: (5) 
6) 
Это интерполяционный многочлен Лагранжа.
Пример. Построить И.М.Л. для функции заданной таблично:
| X | |||
| Y=f(x) |
Интерполяционную формулу Лагранжа можно использовать в более простом виде. Обозначим через: wn+1(x)=(x-x0)*(x-x1)*…*(x-xn)
w’n+1(xi)=(xi-x0)*(xi-x1)*…*(xi-xi-1)*(xi-xi+1)*…*(xi-xn);
(7) 
Если заменить функцию f(x) И.М. Лагренжа, то получим интерполяционную формулу Лагранжа.
(8) f(x)»Ln(x)
Оценка погрешностей И.Ф.Лагренжа производится так: Rn(x)=f(x)-Ln(x)
Разность Rn(x) – остаточный член формулы Лагранжа, его значение равно погрешности при замене функции f(x) значением И.М. Лагранжа.
Пусть функция f(x) имеет на отрезке [a,b], где a=x0, b=xn производные до (n+1)-го порядка включительно. Имеет место следующая формула: (9) 
Формулу (9) можно записать так:
если обозначить максимум производной
Mn+1=xÎ[a,b]max|f(n+1)(x)|, то
(10) 