ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Учебные вопросы
1. Предмет теории вероятностей. Случайные события. Классификация событий.
2. Элементы комбинаторики.
Вопрос 1. Предмет теории вероятностей.
В настоящее время нет практически ни одной области науки, в которой в той или иной степени не применялись бы вероятностные методы.
О.1.1. Теория вероятностей (ТВ) – математическая наука, изучающая закономерности случайных явлений.
При этом изучаемые явления рассматриваются в абстрактной форме, независимо от их конкретной природы. То есть теория вероятностей рассматривает не сами реальные явления, а их упрощенные схемы – математические модели.
Предметом теории вероятностей является изучение математических моделей массовых однородных случайных явлений.
О.1.2. Случайные явления – явления с неопределенным исходом, происходящие при неоднократном воспроизведении определенного комплекса условий.
Примеры случайных явлений:
1. Выпадение орла при подбрасывании монеты.
2. Выигрыш по купленному лотерейному билету.
3. Результат измерения какой-либо величины.
4. Длительность работы телевизора.
Цель теории вероятностей – осуществление прогноза в области случайных явлений, влияние на ход этих явлений, контроль их, ограничение сферы действия случайности.
Вопрос 2. Случайные события. Классификация событий
В естественных науках познание действительности происходит в результате испытаний (экспериментов) или наблюдений, т.е. опыта в широком понимании слова.
О.2.1. Испытание (опыт, эксперимент) – выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат.
Опыт необязательно должен быть поставлен человеком; он может протекать независимо от него; при этом человек выступает в роли наблюдателя или фиксатора происходящего. От него зависит только решение: что именно наблюдать, и какие параметры фиксировать.
О.2.2. Событие – любой исход опыта, который может произойти или не произойти, т.е. качественный результат испытания.
События обозначаются заглавными буквами латинского алфавита: А, В, … или А 1, А 2,….
Пример 1.
Испытание: выстрел по мишени
События (исходы): А = {попадание в мишень}, В = {промах}.
Все события подразделяются на единичные и массовые.
О.2.3. Событие называется единичным, если нельзя повторить опыт, при котором оно произошло.
О.2.4. Событие называется массовым, если условия, при которых оно произошло, можно повторить неограниченное число раз.
О.2.5. Событие называется:
1) достоверным, если оно обязательно произойдет в результате испытания;
2) невозможным, если при испытании оно не может произойти;
3) случайным, если при испытании оно может либо произойти, либо не произойти.
Пример 2.
Испытание: подбрасывание камня
Событие А = {камень упадет} – достоверное
Событие В = {камень улетит} – невозможное
Событие С = {камень пролетит 10 метров} – случайное
О.2.6. Два события называются совместными (несовместными), если при одном испытании появление одного из них не исключает (полностью исключает) появление другого.
Пример 3.
Испытание: стрелок делает 2 выстрела по мишени.
Событие А = {попадание в первый раз}.
Событие В = {попадание во второй раз}.
Событие С = {промах в первый раз}.
События А и В – совместные, а события А и С – несовместные.
О.2.7. Несколько событий образуют полную группу в данном испытании, если в результате испытания непременно должно появиться хотя бы одно из них.
Другими словами, появление хотя бы одного из событий полной группы, есть достоверное событие.
В примере 1 события А и В образуют полную группу.
О.2.8. Два несовместных события, образующих полную группу, называются противоположными или взаимно дополнительными.
В примере 1 события А и В – противоположные.
Событие, противоположное событию А, обозначается Ā.
О.2.9. Несколько событий в данном опыте называются равновозможными, если ни одно из них не является объективно более возможным, чем другие, т.е. все события имеют равные «шансы».
Пример 4.
Испытание: извлечение карты из колоды.
Равновозможные события: А = {туз}, В = {король}, С = {валет}.
Вопрос 3. Элементы комбинаторики
Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики.
Комбинаторика – раздел математики, изучающий количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов заданного конечного множества.
Правила комбинаторики
Пусть А 1, А 2, …, Аk ‒ элементы заданного конечного множества.
Правило суммы
Если элемент А 1 может быть выбран n 1 способами, элемент А 2 ‒ другими n 2 способами, элемент А 3 ‒ отличными от первых двух n 3 способами, …, элемент Аk ‒ nk способами, отличными от всех предыдущих, то выбор одного из элементов: или А 1, или А 2, …., или Аk может быть осуществлен n 1 + n 2 + ….+ nk способами.
Правило произведения
Если элемент А 1 может быть выбран n 1 способами, после каждого такого выбора элемент А 2 может быть выбран n 2 способами, …, после каждого (k-1) выбора элемент Аk может быть выбран nk способами, то выбор всех элементов А 1, А 2, …, Аk в указанном порядке может быть осуществлен
n 1· n 2· … · nk способами.
Основные комбинаторные соединения
Пусть дано множество из n различных элементов. Из этого множества могут быть образованы подмножества (комбинации) из m элементов (0 ≤ m ≤ n).
Различают три типа комбинаций:
· перестановки;
· размещения;
· сочетания.
О.3.1. Перестановками из n различных элементов называются такие комбинации из n элементов, которые отличаются только порядком расположения элементов.
Обозначение числа перестановок: Рn.
Формула: 
Пример 5. Сколькими способами 7 человек могут выстроиться в очередь?
Решение
Р 7 = 7! = 5040.
О.3.2. Если в перестановках из общего числа n элементов есть k различных элементов, при этом первый элемент повторяется n 1 раз, второй элемент ‒ n 2 раз, …., k-й элемент ‒ nk раз (n 1 + n 2 + ….+ nk = n), то такие перестановки называются перестановками с повторениями из n элементов.
Обозначение числа перестановок с повторениями: Рn (n 1, n 2, …, nk)
Формула: 
Пример 6. Сколькими способами можно переставить буквы в слове «МАТЕМАТИКА», чтобы получились всевозможные различные наборы букв?
Решение
Всего букв n = 10.
При этом: «м» ‒ n 1 = 2; «а» ‒ n 2 = 3; «т» ‒ n 3 = 2; «е» ‒ n 4 = 1; «и» ‒ n 5 = 1; «к» ‒ n 6 = 1.
∑ ni = n.
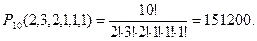
О.3.3. Размещениями из n различных элементов по m в каждом называются такие комбинации из n элементов по m, которые отличаются либо составом элементов, либо порядком их расположения.
Обозначение числа размещений: 
Формула: 
О.3.4. Сочетаниями из n различных элементов по m в каждом называются такие комбинации из n элементов по m, которые отличаются только составом элементов.
Обозначение числа сочетаний: 
Формула: 
Пример 7. Сколькими способами можно выбрать 3 человека на 3 должности из 10 кандидатов, если должности: а) различные, б) одинаковые?
Решение
n = 10, m = 3
а) Порядок следования важен Þ 
б) Порядок следования не важен Þ 
Свойства сочетаний



Размещения с повторениями: 
Сочетания с повторениями: 
Пример 8. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены: а) различные призы, б) одинаковые призы?
Решение
Так как один и тот же фильм может повторяться в номинации несколько раз, то имеем группы с повторениями: а) – размещения; б) – сочетания.

