Приходовский М.А.
Алгебра
(электронное учебное пособие по практике)
ИПМКН ТГУ, группы 932024, 932025
Весна - 2021
ПРАКТИКА 1. 11.2.2021.
Продолжение и повторение за конец 1 семестра.
П. 1. Матрица Грама и её свойства.
Пусть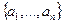 
- система векторов. Матрица, состоящая из всех скалярных произведений:
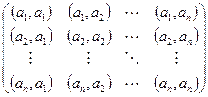
Называется матрицей Грама данной системы векторов. Во-первых, очевидно, что она симметрична.
Свойства.
0. Если система векторов ортогональная, то матрица Грама диагональная.
1. Система векторов является линейно-зависимой тогда и только тогда, когда матрица Грама вырождена.
Пусть система ЛЗС. Тогда какой-либо вектор линейно выражается через остальные. Для определённости обозначений, допустим, что это n-й вектор: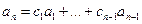 
, тогда последняя строка матрицы представляется в виде линейной комбинации остальных строк, и определитель равен 0:
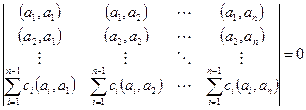
Обратно. Допустим, что определитель Грама равен 0. Тогда есть линейная зависимость между строками, то есть некоторая линейная комбинация всех строк равна нулевой строке.
= 
= 
.
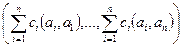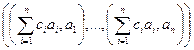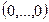Тогда вектор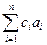 
ортогонален всем векторам из 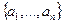. Но он является их линейной комбинацией и принадлежит подпространству, ими порождённому. Поэтому единственная возможность – что сам этот вектор есть 0, то есть 
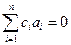, но при этом коэффициенты 
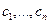не все нулевые, ведь они отражают линейную зависимость строк матрицы Грама. Это означает, что система 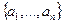ЛЗС.
2. Определитель матрицы Грама неотрицателен.
Если система ЛЗС, то, как выше доказано, он равен 0, значит неотрицателен. Теперь осталось рассмотреть ЛНС .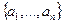
Пусть для начала, это n векторов n-мерного пространства. Тогда матрицу Грама можно представить в виде произведения двух матриц, где в первой векторы 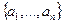расположены по строкам, а во второй по столбцам. Произведения всех строк на столбцы как раз и образуют все скалярные произведения, присутствующие в матрице Грама.
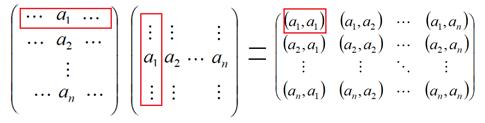
В таком случае, определитель Грамма равен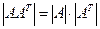 
= 
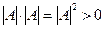. Итак, он равен 0, если система ЛЗС, и больше нуля, если ЛНС.
Теперь рассмотрим систему из k векторов в n-мерном пространстве. В этом случае мы не можем напрямую записать матрицу Грама как произведение двух квадратных матриц, а только как прямоугольных.
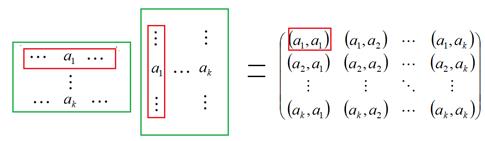
Так как система ЛНС, то линейная оболочка – k-мерное подпространство. В этом случае мы можем достроить до базиса из n векторов, рассмотрев ортонормированную систему из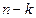 
векторов, ортогональных всем 
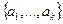. Тогда прямоугольные матрицы будут достроены до квадратных, причём их произведение будет матрицей Грама порядка n с таким строением:
Её определитель больше 0, согласно доказанному выше. Но он равен произведению минора
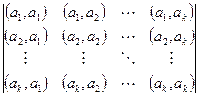на минор Е порядка 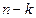, который в свою очередь равен 1. Поэтому указанный минор тоже больше 0.
*
Можно обобщать понятие определителя на прямоугольные матрицы, рассматривая величину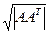 
. При этом необходимо учитывать, что слева должна стоять именно та матрица, у которой число строк меньше числа столбцов. Если наоборот, то произведение 
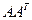будет вырожденной матрицей, так как соответствует системе из n векторов в k-мерном пространстве, при 
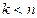такая система ЛЗС.
1 2 1 1 3 5 3 5
1 1 2 1 1 3 2 4
3 1 5 4 10
100 + 60 +60 -50 -80 -90 = 220 – 220 = 0
Пример. Дана система векторов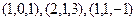 
. Найти определитель матрицы, построенной из них. Найти матрицу Грама и её определитель, сравнить результаты.
= 
= 
.
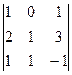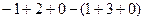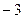Все скалярные произведения найдём с помощью умножения :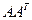
= 
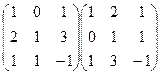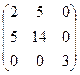- матрица Грама.
Её определитель равен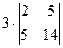 
= 
= 
.
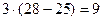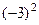п. 2. Проекция вектора на подпространство.
С помощью скалярного произведения можно искать проекцию вектора на подпространство.
Пусть 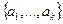- базис k-мерного подпространства в n-мерном пространстве. Вектор 
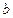не принадлежит подпространству.
Требуется найти вектор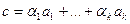 
, такой, что 
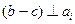для любого номера 
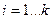. Чертёж:
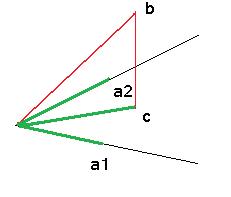
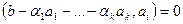для любого i
Если базис 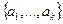является ортогональным, то каждый из коэффициентов 
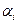определяется отдельно от остальных:
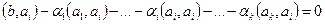, где из-за ортогональности базисных векторов, остаётся лишь одно скалярное произведение, при совпадающих номерах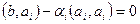 
.
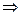
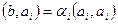
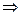
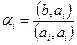В случае, когда базис 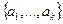не ортогонален, то для нахождения коэффициентов пришлось бы решать систему уравнений:
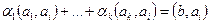, где .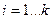
где основная матрица этой системы – это матрица Грама. Поэтому бывает, что лучше сначала ортогонализовать систему (алгоритм ортогонализации Грама-Шмидта был изучен в конце 1 семестра).
Задача. Найти проекцию вектора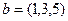 
на плоскость, порождённую векторами 
, 
.
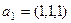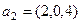Решение. Необходимо найти такую линейную комбинацию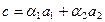 
векторов, 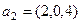, чтобы .
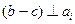Если мы не ортогонализовали систему векторов, то нужно будет решить систему уравнений:
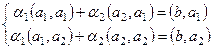
В данном примере она имеет вид:
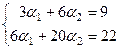
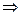
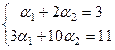
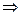
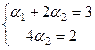
(сократим на общий множитель в каждом, вычтем из второе утроенное первое).
Тогда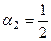 
, и тогда 
.
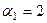Проекцией является вектор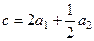 
= 
=
= 
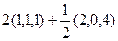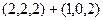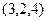. Ответ. Вектор .
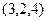Проверка.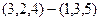 
= 
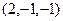. Проверим, что эта разность ортогональна обоим векторам , .
, 
.
- - -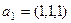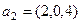
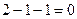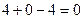