Как мы доказывали в прошлом семестре, элементы обратной матрицы вычисляются по формулам 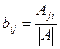 . Однако если мы рассматриваем матрицы не над полем, а над кольцом, то деление на
. Однако если мы рассматриваем матрицы не над полем, а над кольцом, то деление на 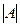 может оказаться невозможным, так как, в отличие от поля, не всякий элемент кольца обратим. Например, в
может оказаться невозможным, так как, в отличие от поля, не всякий элемент кольца обратим. Например, в 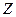 обратимы только 1 и
обратимы только 1 и 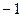 .
.
Матрица 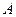 является обратимой над кольцом
является обратимой над кольцом 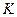 тогда и только тогда, когда
тогда и только тогда, когда 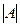 является обратимым элементом в кольце
является обратимым элементом в кольце 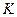 .
.
Задача. Найдите матрицы, обратимые над кольцом целых чисел 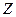 :
:
а) 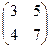 , б)
, б) 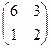 , в)
, в) 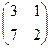 . г)
. г) 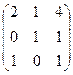 д)
д) 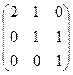
Определители 1, 9, 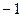 соответственно, поэтому обратимы матрицы в пунктах (а) и (в), не обратима в (б).
соответственно, поэтому обратимы матрицы в пунктах (а) и (в), не обратима в (б).
г) определитель равен 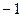 , матрица обратима над
, матрица обратима над 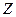 .
.
д) определитель равен 2, матрица не обратима над 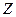 .
.
Элементы теории множеств.
Задача 1. Дано: 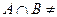 Ø,
Ø, 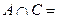 Ø. Возможно ли, что
Ø. Возможно ли, что 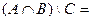 Ø?
Ø?
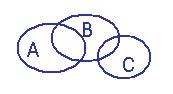
Нет, 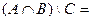
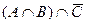 но
но 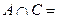 Ø, тогда
Ø, тогда 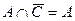 .
.
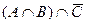 =
= 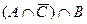 =
= 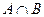 , а про это множество в условии сказано, что оно непусто.
, а про это множество в условии сказано, что оно непусто.
Задача 2. Доказать, что
1) 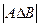 =
= 
2) 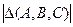 =
= 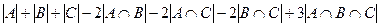
(множество элементов, принадлежащих лишь одному из множеств).
2а) 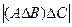 =
= 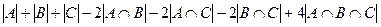
n=2 очевидно: 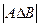 =
=  при объединении, все элементы пересечения учтены 2 раза, их и нужно вычесть.
при объединении, все элементы пересечения учтены 2 раза, их и нужно вычесть.
n=3: два разных подхода к образованию симметрической разности.
А) Если определять 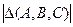 как множество элементов, принадлежащих только одному из множеств:
как множество элементов, принадлежащих только одному из множеств:
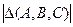 =
= 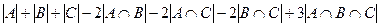
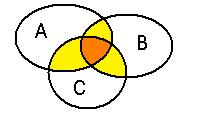
центральную часть прибавили 3 раза, вычли 6 раз, значит, нужно прибавить 3 раза, чтобы характеристическая функция приняла значение 0.
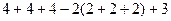 = 3, в симметрической разности тоже 3 точки.
= 3, в симметрической разности тоже 3 точки.
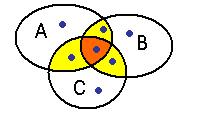
Б) Если последовательно, то
 =
= 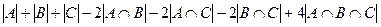
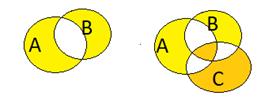
В этом случае центральная часть присутствует, и её характеристическую функцию нужно прибавить 4 раза.
Задача 3. Доказать, что 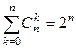 .
.
Идея решения: Множество всех подмножеств из k элементов, при всех k, как раз и составляет множество всех подмножеств.
Задача 4. Дано универсальное множество 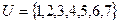 и множества
и множества 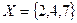 ,
, 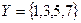 ,
, 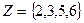 .
.
1) Найти множество 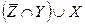 .
.
2) Записать булеан множества 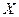 .
.
Решение.
1) 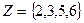
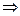
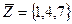 .
.
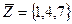
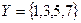
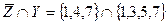 =
= 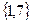 .
.
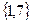
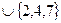 =
= 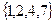 .
.
2) Множество всех подмножеств 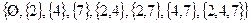 .
.
Задача 5. Из 100 студентов факультета, в олимпиаде по математике участвовали 28, по физике 42, по информатике 30. Одновременно в двух олимпиадах участвовали: по математике и физике 10 студентов, по математике и информатике 8 студентов, по физике и информатике 5 человек. При этом во всех трёх олимпиадах приняли участие 3 человека. Сколько студентов не участвовали ни в одной олимпиаде?
Решение. По формуле включений и исключений,
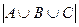 =
= 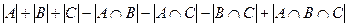 .
.
Найдём число студентов, которые участвовали хотя бы в одной олимпиаде. 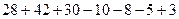 =
= 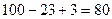 .
.
Таким образом, 20 студентов не участвовали ни в одной олимпиаде.
Практика 3
Задача 6 (РП). На кафедре 13 человек знают иностранные языки. Причём каждый из них владеет хотя бы одним иностранным языком. 10 человек знают английский, 7 человек немецкий, 6 французский. При этом 5 человек знают английский и немецкий, 4 знают английский и французский, 3 знают немецкий и французский.
1) Сколько человек знают 3 языка?
2) Сколько человек знают только 2 языка?
3) Сколько человек знают только английский?
Решение.
По формуле включений и исключений,
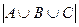 =
= 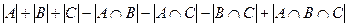 .
.
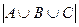 = 13.
= 13. 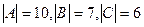 .
.
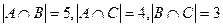 .
.
Тогда число людей, знающих все 3 языка, 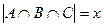 .
.
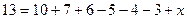
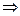
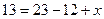
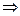
 .
.
Англ+нем: всего 5 чел, из них 2 знают и третий язык, т.е. только англ+нем 3.
англ + фр 4, только англ + фр 2
нем + фр 3, только нем + фр 1.
Далее, англ 10, вычесть 3,2,2. Остаётся 3 - только англ.
Аналогично, нем 7, вычесть 3,1,2, осталось 1.
фр 6, вычесть 2,1,2, осталось 1.
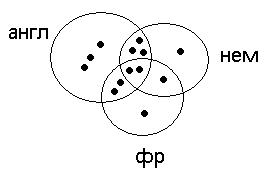
1) Сколько человек знают 3 языка? 2
2) Сколько человек знают только 2 языка? 6
3) Сколько человек знают только английский? 3
Задача 7.
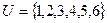 ,
, 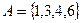 ,
, 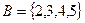 ,
, 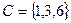 .
.
Найти 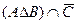 . В ответе указать сумму и произведение всех чисел этого множества, а также мощность множества.
. В ответе указать сумму и произведение всех чисел этого множества, а также мощность множества.
Решение.
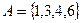 ,
, 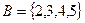
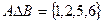 . Учитываем элементы, которые есть только в одном или другом множестве. 3 и 4 есть в обоих множествах, поэтому в симметрическую разность они не входят.
. Учитываем элементы, которые есть только в одном или другом множестве. 3 и 4 есть в обоих множествах, поэтому в симметрическую разность они не входят.
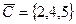 .
.
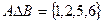 ,
, 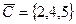 . Пересечение
. Пересечение 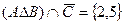 .
.
Ответ. 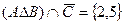 , сумма чисел равна 7, произведение 10, мощность 2.
, сумма чисел равна 7, произведение 10, мощность 2.
Задача 8.
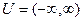 ,
, 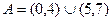 ,
, 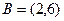 ,
, 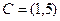 .
.
Найти 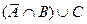 .
.
Решение.
1) 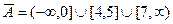 .
.
2) 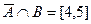
3) 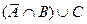 =
=  .
.
Задача 9.
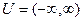 ,
, 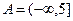 ,
, 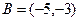 ,
, 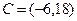 .
.
Найти 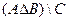 .
.
Решение.
Так как 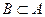 то
то 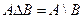 =
= 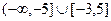 .
.
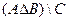 =
=  .
.
Ответ. 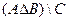 =
=  .
.
Задача 9-А
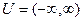 ,
, 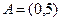 ,
, 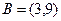 ,
, 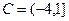 .
.
Найти 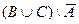 .
.
Решение. 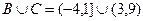 .
.
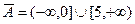
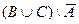 =
= 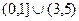 .
.
Перерыв
Задача 10. (Принцип индукции). Доказать, что 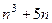 делится на 6 для любого
делится на 6 для любого 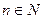 .
.
База индукции. 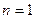 .
. 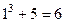 .
.
Индукционный шаг. Пусть верно для n, рассмотрим n+1.
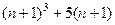 =
= 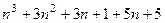 =
= 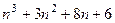 .
.
Выделим старое выражение отдельным слагаемым, а также константу, которая точно делится на 6.
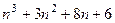 =
= 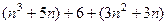 . Осталось доказать, что последнее слагаемое делится на 6. Оно точно делится на 3, поэтому осталось доказать, что
. Осталось доказать, что последнее слагаемое делится на 6. Оно точно делится на 3, поэтому осталось доказать, что 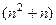 делится на 2.
делится на 2.
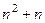 =
= 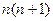 произведение соседних целых чисел, поэтому одно из них точно чётное, значит,
произведение соседних целых чисел, поэтому одно из них точно чётное, значит, 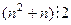 ,
, 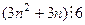 .
.
Задача 11. (Принцип индукции). Доказать, что при любом натуральном 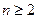 верно
верно 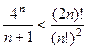 .
.
Решение.
Проверим при 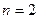 (база индукции).
(база индукции).
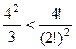
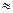
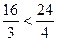
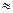
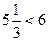 . (При n=3: 16 < 20).
. (При n=3: 16 < 20).
Если верно при n, докажем, что и при 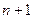 .
.
Составим выражение при 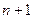 и докажем, что левая часть умножается на меньший коэффициент, чем правая.
и докажем, что левая часть умножается на меньший коэффициент, чем правая.
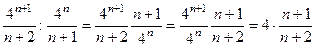 =
= 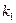 (для левой).
(для левой).
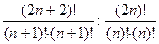 =
= 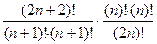 =
= 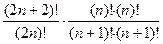 =
= 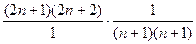 =
=
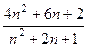 =
= 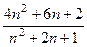 =
= 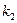 =
= 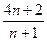 (для правой).
(для правой).
Соотношение.
 =
= 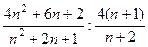 =
= 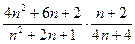 =
=
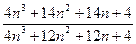 . В выражении
. В выражении 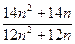 числитель больше знаменателя. Тогда
числитель больше знаменателя. Тогда 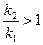 . Неравенство сохранится при переходе от n к n+1.
. Неравенство сохранится при переходе от n к n+1.
Если сократить ранее, то 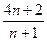
 =
=  =
= 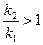 .
.
Задача 12. Доказать, что множества  и
и 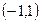 равномощны. Построить биективное отображение.
равномощны. Построить биективное отображение.
Решение.  биективно отображает
биективно отображает  на
на
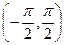 . Тогда
. Тогда 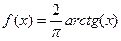 биекция
биекция  на
на 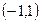 .
.
Задача 12-А. Доказать, что множества  и
и 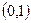 равномощны. Построить биективное отображение.
равномощны. Построить биективное отображение.
Как и в прошлой задаче, но 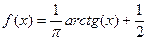 (прошлую функцию сжать в 2 раза и поднять на 0,5).
(прошлую функцию сжать в 2 раза и поднять на 0,5).
Задача 13 (РП). Доказать, что любые два интервала 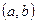 и
и 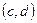 на прямой равномощны.
на прямой равномощны.
Решение. 2 способа:
1) Построить биекцию.
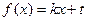 ,
, 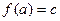 ,
, 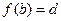 .
.
Получится система уравнений 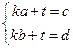
Вычесть 1-е из 2-го 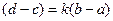 ,
, 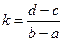 ,
,
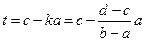 . Биективное отображение существует.
. Биективное отображение существует.
2) По теореме Кантора-Бернштейна.
Построить 2 инъективных отображения, 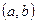 в
в 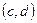 и
и 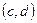 в
в 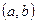 .
.
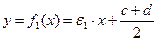 ,
, 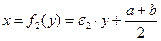 . (малые коэфф, кратно меньше отношения длин интервалов). Каждое множество равномощно подмножеству второго, эти множества равномощны.
. (малые коэфф, кратно меньше отношения длин интервалов). Каждое множество равномощно подмножеству второго, эти множества равномощны.
ПРАКТИКА 4. 20.2.2021.
Задача 13. Доказать, что множества 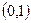 и
и 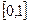 равномощны.
равномощны.
Решение. 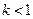 ,
,
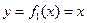 ,
, 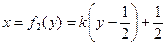 .
.
Каждое множество отображается на часть второго с помощью инъективной функции.
По теореме Кантора-Бернштейна, они равномощны, континуум.
Задача 14. Доказать, что множества 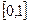 и
и 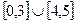 равномощны.
равномощны.
Решение.
Два инъективных отображения: 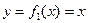 .
.

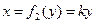 .
.
По теореме Кантора-Бернштейна, они равномощны.
Задача 15. Найти мощность множества корней уравнения 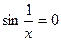 .
.
Решение. 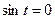
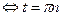 ,
, 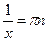 ,
, 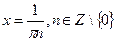 .
.
Существует биективное отображение между множеством корней этого уравнения и 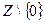 , а это счётное множество.
, а это счётное множество.
Графики функций 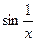 и
и 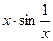 выглядят так:
выглядят так:
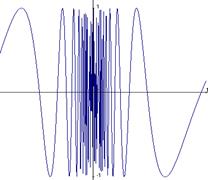 и
и 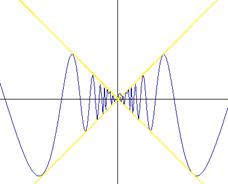
Задача 16. Доказать, что если  - множества корней многочленов
- множества корней многочленов 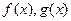 соответственно, то
соответственно, то 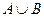 - множество корней произведения многочленов
- множество корней произведения многочленов 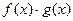 .
.
Решение. 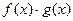 = 0 тогда и только тогда, когда один или второй множитель равен 0,
= 0 тогда и только тогда, когда один или второй множитель равен 0, 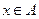 или
или 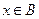 , то есть
, то есть 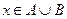 .
.
Задача 17. На множестве 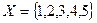 задано бинарное отношение:
задано бинарное отношение: 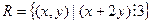 . Представить с помощью графа и матрицы, выяснить свойства (рефлексивность, симметричность, транзитивность), является ли отношением эквивалентности или отношением порядка?
. Представить с помощью графа и матрицы, выяснить свойства (рефлексивность, симметричность, транзитивность), является ли отношением эквивалентности или отношением порядка?
Решение.
Рефлексивность очевидна: для пары 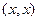 получается
получается 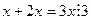 .
.
Симметричность: 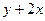 =
= 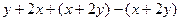 =
=
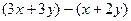 , и здесь каждое делится на 3.
, и здесь каждое делится на 3.
Транзитивность: пусть 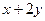 и
и 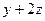 делятся на 3, проверим это свойство для
делятся на 3, проверим это свойство для 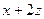 .
.
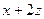 =
= 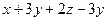 =
= 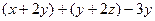 , здесь каждое делится на 3. Значит, отношение транзитивно.
, здесь каждое делится на 3. Значит, отношение транзитивно.
Итак, это отношение эквивалентности (рефлексивно, симметрично, транзитивно).
Запишем сами эти числа вида 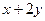
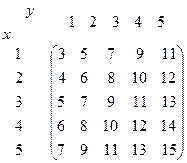
Укажем «1», где делится на 3:
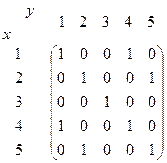
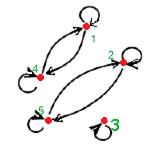
Граф отношения:
Из строения матрицы видно, что отношение рефлексивно и симметрично. Отношение эквивалентности.
Классы эквивалентности 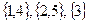 видны на графе (множество распадается на 3 непересекающихся подмножества).
видны на графе (множество распадается на 3 непересекающихся подмножества).
Подматрицы из 1,4 строки и 1,4 столбца,
2,5 строка и 2,5 столбец, 3 строка 3 столбец.
В 1,4 строках не содержится «1» нигде кроме этих же номеров столбцов.
- Перерыв -
Задача 18. Фундированные множества (задача с монетами).
Каждую минуту автомат меняет монету, выдавая любое количество любых монет, но меньшего достоинства (видов монет конечное число). Доказать, что рано или поздно у игрока не останется ни одной монеты.
Решение. Пусть есть k видов монет. Множество монет, имеющееся в определённый момент, можно описать набором чисел 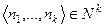 .
.
Отношение порядка введём следующим образом.
Если 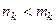 то
то 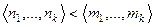 ,
,
Если 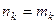 то сравнение по
то сравнение по 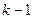 номеру и так далее.
номеру и так далее.
Набор 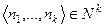 при каждом действии уменьшается (в смысле введённого порядка). При этом множество
при каждом действии уменьшается (в смысле введённого порядка). При этом множество 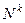 фундировано (доказано в лекциях). Таким образом, процесс должен оборваться.
фундировано (доказано в лекциях). Таким образом, процесс должен оборваться.
.
Задача 19. (РП). Пусть X и Y - два непересекающихся частично упорядоченных множества. На их объединении задан частичный порядок: внутри каждого множества элементы сравниваются как и прежде, а любой элемент 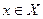 по определению меньше любого элемента
по определению меньше любого элемента 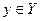 . Будет ли такой порядок линейным? Почему?
. Будет ли такой порядок линейным? Почему?
Частичный порядок, следовательно, 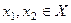 или
или 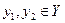 несравнимые в исходном множестве, и после объединения будут несравнимы.
несравнимые в исходном множестве, и после объединения будут несравнимы.
Задача 20. Доказать, что 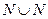 можно вполне упорядочить.
можно вполне упорядочить.
Решение. 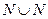 (это не декартово произведение)
(это не декартово произведение) 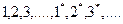 , порядок:
, порядок: 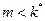 .
.
 предельный элемент (не существует непосредственного предшествующего).
предельный элемент (не существует непосредственного предшествующего).
Линейный порядок был на каждом из множеств, линейный порядок на объединении. Кроме того, множество фундированное.
(1 есть наименьший элемент). Линейно упорядоченное и фундированное, значит, вполне упорядоченное.
Задача 21. Доказать методом математической индукции, что
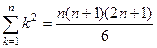 .
.
Решение. База индукции. Можно непосредственно проверить на малых числах, например 1 или, если интересно, 2 (достаточно 1).
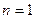 .
. 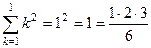 .
.
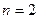 .
. 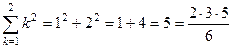 .
.
Индукционный шаг. Рассмотрим, следует ли из выполнения этого равенства для номера 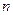 его выполнение для номера
его выполнение для номера 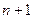 .
.
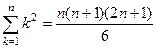 ,
, 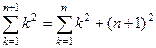 =
=
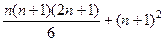 .
.
С другой стороны, для 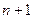 выражение бы выглядело так:
выражение бы выглядело так: 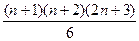 .
.
Мы должны убедиться, что:
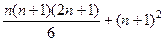 =
= 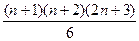 .
.
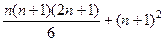 =
= 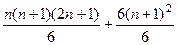 , таким образом, остаётся сравнить
, таким образом, остаётся сравнить 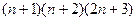 и
и 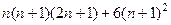 .
.
Сократим на 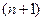
сравнить 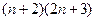 и
и 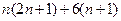 .
.
Справа и слева 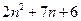 .
.
Задача 22. Доказать методом математической индукции, что
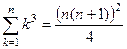 .
.
Решение. База индукции. 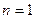 .
. 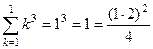 .
.
Индукционный шаг. Рассмотрим, следует ли из выполнения этого равенства для номера 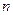 его выполнение для номера
его выполнение для номера 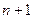 .
.
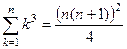 ,
, 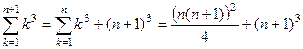 .
.
С другой стороны, для 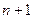 выражение бы выглядело так:
выражение бы выглядело так:
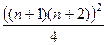 .
.
Нужно сравнить 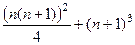 и
и 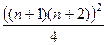 .
.
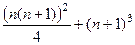 =
= 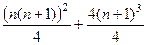 .
.
Остаётся сравнить 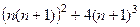 и
и 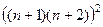 .
.
Сократим 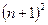 . Остаётся сравнить:
. Остаётся сравнить: 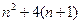 и
и 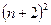
оба равны  .
.
Практика 5.
(из рабочей программы):
