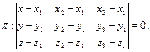Возьмем на плоскости линию 2-го порядка (ЛВП), заданную уравнением (27.1) и прямую 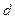 , заданную параметрическим уравнением:
, заданную параметрическим уравнением:
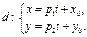
| (27.2) |
Найдем точки пересечения прямой и ЛВП (обозначим 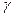 ), для этого решим систему уравнений (27.1) и (27.2). Подставим
), для этого решим систему уравнений (27.1) и (27.2). Подставим 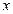 и
и 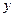 из (27.2) в (27.1), получим
из (27.2) в (27.1), получим
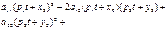
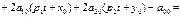
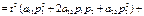
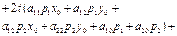
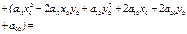
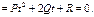
Исследуем полученное квадратное уравнение. Рассм. cлучаи:
1. Если 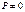 , тогда рассмотрим дискриминант
, тогда рассмотрим дискриминант 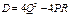 .
.
a. Если 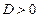 , тогда прямая
, тогда прямая 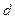 пересекает
пересекает 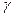 в 2 точках.
в 2 точках.
b. Если 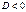 , то общих точек у прямой и ЛВП нет.
, то общих точек у прямой и ЛВП нет.
c. Если 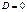 , то прямая
, то прямая 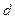 пересекает
пересекает 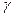 в 1 точке (2 совпавшие точки пересечения).
в 1 точке (2 совпавшие точки пересечения).
2. Если 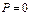 , тогда ур-е принимает вид
, тогда ур-е принимает вид 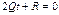 .
.
a. Пусть 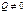 , тогда
, тогда 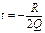 , т.е. прямая пересекает ЛВП в 1 точке.
, т.е. прямая пересекает ЛВП в 1 точке.
b. Пусть 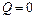 и
и 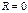 , то
, то 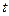 - любое, т.е.
- любое, т.е. 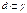 .
.
c. Пусть 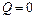 и
и 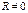 , тогда
, тогда 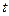 - любое, т.е.
- любое, т.е.  .
.
5. Направление, определяемое ненулевым вектором 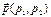 , называется асимптотическим направлением относительно линии
, называется асимптотическим направлением относительно линии 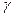 , если прямая, параллельная вектору
, если прямая, параллельная вектору 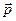 , либо имеет с линией не более одной общей точки, либо содержится в линии
, либо имеет с линией не более одной общей точки, либо содержится в линии 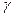 . Направление называется асимптотическим т.т., когда
. Направление называется асимптотическим т.т., когда 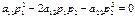 .
.
Выясним кол-во асимптотических направлений для каждой прямой. Запишем уравнение: 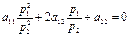 , откуда
, откуда 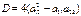 . Значит,
. Значит,
1) Если 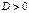 , то
, то 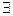 2 асимптотических направления (линия гиперболич. типа);
2 асимптотических направления (линия гиперболич. типа);
2) Если 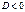 , то нет асимптотических направлений (линия эллиптич. типа);
, то нет асимптотических направлений (линия эллиптич. типа);
3) Если 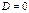 , то
, то 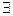 1 асимптотическое направление (линия параболич. типа).
1 асимптотическое направление (линия параболич. типа).
Точка ЛВП называется ее особой точкой, если она является ее центром симметрии.
Прямая называется касательной к ЛВП в ее неособой точке, если она пересекает ее в 2-х совпавших точках.
Напишем уравнение прямой 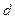 , проходящей через точку
, проходящей через точку  и заданной уравнением (27.2). Подставим (27.2) в (27.1), получим (см. выше):
и заданной уравнением (27.2). Подставим (27.2) в (27.1), получим (см. выше):
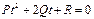 , т.к.
, т.к.  , то
, то 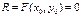 . Тогда получим, что
. Тогда получим, что 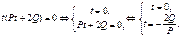 Решением этого уравнения будут 2 совпавших корня
Решением этого уравнения будут 2 совпавших корня 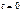 т.т.т., когда
т.т.т., когда 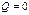 . Т.о., прямая, заданная направляющим вектором
. Т.о., прямая, заданная направляющим вектором 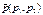 и точкой
и точкой  будет касательной к линии
будет касательной к линии 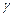 в т.
в т. 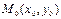 , если
, если 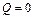 , т.е.
, т.е. 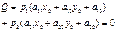 .
.
6. Теорема 2. В каждой обыкновенной точке ЛВП существует одна и только одна касательная. Если линия задана общим уравнением (27.1), то касательная в точке 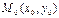 этой линии имеет уравнение:
этой линии имеет уравнение:
 . Касательная к эллипсу:
. Касательная к эллипсу: 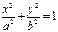 в точке
в точке 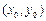 . Здесь
. Здесь 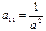 ,
, 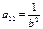 ,
, 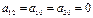 ,
, 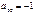 , поэтому уравнение примет вид:
, поэтому уравнение примет вид: 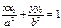 .
.
Касательная к гиперболе: 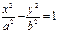 в точке
в точке 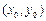 . Очевидно, имеет вид
. Очевидно, имеет вид 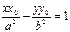 .
.
Касательная к параболе: 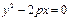 в точке
в точке 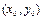 . Итак,
. Итак, 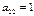 ,
, 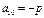 ,
, 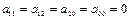 , поэтому уравнение примет вид:
, поэтому уравнение примет вид: 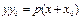 .
.
7. Диаметры ЛВП. Возьмем на плоскости некоторую ЛВП, заданную общим уравнением (27.1). назовем хордой этой линии отрезок, концы которого принадлежат этой линии.
Теорема 3. Если задан вектор 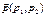 , имеющий не асимптотическое направление относительно ЛВП
, имеющий не асимптотическое направление относительно ЛВП 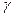 , то точка
, то точка 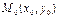 будет серединой хорды, параллельной вектору
будет серединой хорды, параллельной вектору 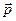 т.т.т., когда
т.т.т., когда 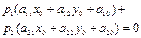 .
.
Возьмем множество всех середин хорд, полученных при пересечении прямых, параллельных вектору 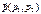 , с
, с 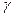 , тогда для каждой середины
, тогда для каждой середины 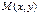 будет выполняться равенство:
будет выполняться равенство:
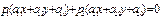 или
или
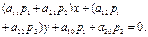
| (27.3) |
Диаметр, сопряженный вектору 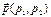 , относительно ЛВП заданной общим уравнением, определяется уравнением (27.3).
, относительно ЛВП заданной общим уравнением, определяется уравнением (27.3).
Пусть 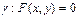 - линия 2-го порядка. Вектор
- линия 2-го порядка. Вектор 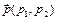 - вектор неасимптотического направления для кривой
- вектор неасимптотического направления для кривой 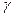 . Множество середин хорд, параллельных вектору
. Множество середин хорд, параллельных вектору 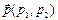 , называется диаметром кривой 2-го порядка, сопряженным вектору
, называется диаметром кривой 2-го порядка, сопряженным вектору 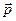 .
.
Два диаметра называются сопряженными относительно ЛВП, если каждый из них делит пополам хорды, параллельные другому диаметру.
Направление вектора 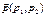 называется сопряженным направлению вектора
называется сопряженным направлению вектора 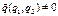 , если выполняется равенство:
, если выполняется равенство:
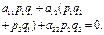
| (27.4) |
Направление называется главным относительно ЛВП, если оно сопряжено с перпендикулярным направлением.
Пусть вектор 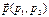 имеет главное направление. Возьмем один из перпендикулярных ему векторов
имеет главное направление. Возьмем один из перпендикулярных ему векторов 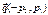 . Тогда для этих векторов выполняется условие (27.4), которое будет иметь вид:
. Тогда для этих векторов выполняется условие (27.4), которое будет иметь вид: 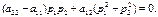 Получено условие для нахождения координат вектора главного направления.
Получено условие для нахождения координат вектора главного направления.
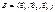 - некоторый базис 3-х мерного векторного пространства, то
- некоторый базис 3-х мерного векторного пространства, то 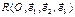 называется аффинной системой координат (АСК) в пространстве. Вектор ОМ называется радиус-вектором точки М (относительно точки О). Если вектор
называется аффинной системой координат (АСК) в пространстве. Вектор ОМ называется радиус-вектором точки М (относительно точки О). Если вектор 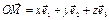 , то числа
, то числа 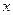 ,
, 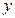 и
и 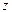 называются координатами точки М в системе координат
называются координатами точки М в системе координат 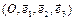 .
АСК называется прямоугольной декартовой иобозначается
.
АСК называется прямоугольной декартовой иобозначается 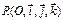 , если базис
, если базис 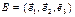 - ортонормированный.
Метод координат состоит в изучении геометрических фигур с помощью алгебры (аналитически) на основе применения координат. Фигура – это любое множество точек.
Уравнением, определяющим некоторую фигуруF в пространстве в заданной АСК
- ортонормированный.
Метод координат состоит в изучении геометрических фигур с помощью алгебры (аналитически) на основе применения координат. Фигура – это любое множество точек.
Уравнением, определяющим некоторую фигуруF в пространстве в заданной АСК 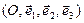 , называется уравнение, которому удовлетворяют координаты всех точек, принадлежащих F и не удовлетворяют координаты точек, не принадлежащих F.
Возьмем в пространстве некоторую плоскость π, рассмотрим множество всех векторов параллельных ей, они образуют двумерное векторное подпространство, которое называется направляющим подпространством плоскости π. Обозначается L Возьмем любые 2 вектора
, называется уравнение, которому удовлетворяют координаты всех точек, принадлежащих F и не удовлетворяют координаты точек, не принадлежащих F.
Возьмем в пространстве некоторую плоскость π, рассмотрим множество всех векторов параллельных ей, они образуют двумерное векторное подпространство, которое называется направляющим подпространством плоскости π. Обозначается L Возьмем любые 2 вектора 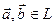 , где
, где 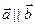 ,
, 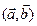 - базис L. Пусть задана т.
- базис L. Пусть задана т. 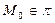 , тогда
, тогда 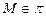 т.т.т., когда векторы.
т.т.т., когда векторы. 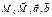 - компланарны, т.е.
- компланарны, т.е. 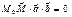 Введем АСК
Введем АСК 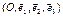 и
и 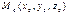 ,
, 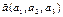 ,
,  . Обозначим
. Обозначим 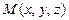 . Тогда уравнение плоскости π будет иметь вид:
. Тогда уравнение плоскости π будет иметь вид:
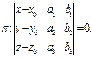
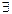 числа
числа 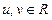 такие, что
такие, что 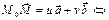
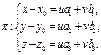
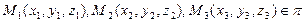 . Этот случай можно свести к 1-му способу задания плоскости. Тогда ур-е плоскости будет иметь вид:
. Этот случай можно свести к 1-му способу задания плоскости. Тогда ур-е плоскости будет иметь вид: