Рассмотрим 2 прямые: 
и 
, заданные точкой и вектором. Т.о., имеется тройка векторов 
.
Рассмотрим случаи:
1) Если смешанное произведение 
, то прямые 
и 
скрещивающиеся.
2) Если 
, 
и 
, то прямые и параллельны.
3) Если векторы 
- компланарны, т.е. 
и 
, тогда прямые и пересекаются в одной точке.
4) Если 
, то прямые и совпадают.
Пример. Определить взаимное расположение 2 прямых в АСК, если 
и 
Решение. Векторы 
, 
. Точки 
и 
(при 
). Тогда 
. Исследуем на коллинеарностьвекторы 
и 
. Рассмотрим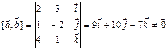 
т.о., векторы и не коллинеарны. Значит прямые пересекаются в точке или скрещиваются. Рассмотрим смешанное произведение: 
, значит, прямые и пересекаются в одной точке.
абелева группа
2) 
3) 
4) 
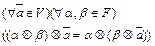5) 
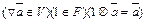Подпр. ВП V над R наз-ся непустое подмн. V0 множестваV, кот. само обр. пр-во отн. тех же опер. над тем же полем.
Для того чтобы подмножество V0 ВП V было его подпр., дост. выполнения условий:1) 
; 2) 
.
Лин. комб. в-в 
наз-ся сумма вида 
, где 
.
Линейной оболочкой, порожденной сист в-в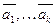 
с коэф 
наз-ся мн всех лин. комб этих в-в. Обозн. 
Конечномерным векторным пространством V над полем F называется векторное пространство, порождаемое конечной системой векторов.
Сист в-в 
не все = нулю, такие что 
.
Сист в-в 
из того что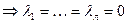 
.
Базисом конечномерной системы векторов называется непустая линейно независимая ее подсистема, если каждый вектор системы можно выразить линейно через подсистему.
Базисом конечномерного векторного пространства V надF называется непустая конечная ЛНЗ сист в-в 
.
Размерностью ненулевого конечномерного ВП называется число векторов его базиса. Обозн.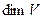 
.
Th.(о разложении вектора по базису)
Пусть V – конечномерное векторное пространство над полем F, 
существует единственное разложение по базису.
□ (сущ-е)По условию V – конечномерное в.п., тогда оно порождается базисом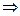 
любой вектор из V можно выразить через линейную комбинацию векторов базиса, т.е. 
, где 
.
(ед-ть)Предположим, что существует два разложения 
и 
вычтем одно из другого 
Т.к. 
разложение единственно.■
), кот. при подстановке в каждое уравнение системы, обращает его в верное равенство.
Если система (1) имеет хотя бы 1 решение, то она называется совместной. Если система (1) не имеет решения, то она называется несовместной
Если система (1) обладает единственным решением, то она называется определенной, если она имеет больше, чем одно решение, то она называется неопределенной.
Для любой системы возможны только 3 случая:
1) система несовместна, то есть не имеет решения
2) система совместна и определена, то есть имеет единственное решение
3) система совместна и не определена, то есть имеет бесконечно много решений.
Сист. наз-ся ступенчатой при выполнении следующих условий: если некоторое уравнение начинается с переменной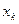 
, то каждое следующее уравнение начинается с переменной с большим номером.
Переменные, с которых начинаются ур. ступенчатой сист. наз-ся главными, остальные свободными.
Уравнение вида: 
называется протеворечивым уравнением.
Две СЛУ наз-ся~, если они или обе несовместны, или обе совместны и обл. одними и теми же решениями.
Две СЛУ наз-ся равносильными, если каждое решение одной из них явл. решением другой и наоборот.
Элементарными преобразованиями СЛУ называются:
1) перестановка уравнений местами или переменных в каждом уравнении;
2)умножение обеих частей уравнения на 
3)прибавление к обеим частям одного из уравнений системы соответственных частей другого уравнения, умноженного на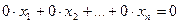 
Th. (Кронекера – Капелли) СЛУ совместна ór(A)=r(Aрасш).
Метод Гаусса.
Рассмотрим СЛУ (1).Пусть 
, подберем множители 
так, чтобы умножив 
на эти множители и сложив с другими уравнениями, под 
получились бы нулевые коэффициенты, т.е. исключим переменную 
и аналогично исключим переменную 
из всех уравнений, начиная с третьего и т.д.Через s шагов получим
Если СЛУ совместна, то при помощи цепочки элементарных преобразований ее можно привести к ступенчатому виду:
1) если s=n, то СЛУ имеет единственное решение.
2) Если s<n, то СЛУ имеет 
число решений. Необходимо выбрать (n-s) свободных переменных, а остальные s (главные) выразить через свободные.
Матричный метод.
Запишем СЛУ в виде AX=B, A – осн матрица, Х – столбец переменных, В – столбец свободных членов.
Пусть СЛУ дана в матричном виде и строки матрицы А линейно независимы, тогда СЛУ имеет единственное решение 
.
□(сущ-е): Подставим 
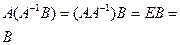Чтобы матрица А была обратима необходимо, чтоб А была квадратной, строки А были лнз. 
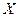имеет вид 
■
Метод Крамера.
Пусть А квадратная матрица n-го порядка – основная матрица СЛУ (1). Если 
, то СЛУ (1) имеет!решение: 
, где 
- определитель основной матрицы А, 
- определитель матрицы, полученной из основной путем замены i-ого столбца на столбец свободных членов.