Основные свойства функции

Числовой функцией с областью определения D называется соответствие при которой каждому числу х из множества D сопоставляется по некоторому правилу число у зависящее от х.

Чтобы показать, что у есть функция переменной х, пользуют­ся символическими записями: y=f(x), y=j(x), y=F(x) и т. д.

Такая символическая запись не раскрывает самого правила зависимости у от х, и лишь устанавливает сам факт наличия зависимости.

Под областью определения (существования) функции f(х) понимается совокупность всех действительных значений аргу­мента х, при которых функция определена и выражается действи­тельным числом.

Отметим особенности отыскания области определения неко­торых функций.

1. При отыскании области определения дробной функции нужно исключить значения аргумента, при которых знаменатель обращается в нуль.

2. Если аналитическое выражение функции содержит корень четной степени, то при отыскании области определения функции нужно исключить значение аргумента, при которых подкоренное выражение принимает отрицательное значения.

3. Если аналитическое выражение функции содержит логарифм, то при отыскании области определения данной функции нужно исключить значение аргумента, при которых выражение под знаком логарифма принимает отрицательные значения и обращается в нуль.

4. Если аналитическое выражение функции содержит обратные тригонометрические функции арксинус или арккосинус, то при нахождении области ее определения нужно включить только те значения аргумента, при которых выражения, стоящие под знаком этих функций, по модулю не превосходят единицы.

Область значений функции есть множество всех действитель­ных значений, которые принимает функция.

Способы задания функции

Функция считается заданной, если известна область опреде­ления функции и указано правило, по которому для каждого значения аргумента можно найти соответствующее значение функции. Такое правило можно указать различными способами; из них наиболее распространенными являются табличный, гра­фический и аналитический.

Табличный способ состоит в том, что значения аргумента и соответствующие им значения функции записаны в виде таб­лицы.

Табличный способ широко используется на практике для записи результатов наблюдений и измерений.

Несмотря на простоту, такой способ задания функции не дает полного представления о характере функциональной зависи­мости между х и у, лишен наглядности. Однако иногда это един­ственный способ выражения функциональной зависимости.

Если же функция изображена в прямоугольной системе коор­динат в виде графика, т. е. какой-то линии, где абсцисса каждой точки является аргументом, а ордината — функцией, то такой способ задания функции называется графическим. Графический способ задания функции удобен своей наглядностью при изучении различных процессов. На графике часто видны такие осо­бенности поведения функции, которые трудно установить при других способах задания функции. Иногда этот способ выражения зависимости между аргумен­том и функцией является единственно возможным, иногда же он применяется в качестве дополнительного — для наглядного изоб­ражения характера функциональной зависимости.

При аналитическом способе зависимость между аргументом х и функцией у задается в виде математической формулы или уравнения. В этой формуле указаны действия, которые нужно произвести над значением аргумента, чтобы получить соответ­ствующее значение функции. Придавая аргументу х различные значения, мы можем вычислить соответствующее значение у с необходимой точностью.

Единственный недостаток аналитического способа — отсутст­вие наглядности. В математике предпочтение отдается этому способу. Зная закон соответствия у=f(х), всегда можно соста­вить таблицу и построить график. Другие способы задания функ­ции такой универсальностью не обладают. На практике при ис­следовании различных зависимостей наиболее удобными явля­ется сочетание различных способов заданий функции.

Основные свойства функций

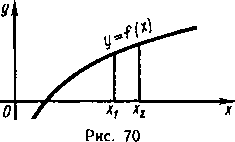
Функций у=f(х) называется возраста­ющей на некотором интервале, если для любых х из этого интервала большему значению аргумента соответствует большее значение функции, т. е. при x₁<x₂ имеет место неравенство f(x₁)>f(x₂) (рис.1).

Функция у=f(х) называется убывающей на некотором интервале, если для любых х из этого интервала большему значению аргумента соответствует меньшее значение функции, т. е. при x₁<x₂ имеет место неравенство f(x₁)>f(x₂) (рис.2).

Если же для любых значений х, взятых из некоторого проме­жутка и удовлетворяющих условию x₁<x₂ вытекает нестрогое неравенство f(x₁≤f(x₂) или f(x₁)≥f(x₂), то функция называется неубы­вающей (невозрастающей). Функции только убывающие или толь­ко возрастающие называются монотон­ными.

Функция у=f(х) называется кусочно-монотонной в данном промежутке, если этот промежуток можно разбить на конечное число промежутков, в каждом из которых функция монотонна.

При исследовании поведения функции вблизи некоторой точки удобно пользоваться понятием окрестности. Окрестностью точки А называют любой интервал содержащий эту точку.

Точка х₀ называется точкой минимума функции f, если для всех х из окрестности х₀ выполнено неравенство f(x) ≥ f(х₀).

Точкой х₀ называют точкой максимума функции f, если для всех х из некоторой окрестности х₀ выполняется неравенство f(x) ≤ f(х₀).

Для точек max и min функции принято общее название – их называют точками экстремума.

Функция у=f(х) называется четной, если при изменении знака у любого значение аргумента, взятого из области определения функции, значения функ­ции не изменяются, т. е. f(-x)=f(x).

Функция у=f(х) называется нечетной, если при изме­нении знака у любого значения аргумента, взятого из об­ласти определения функции, значения функции изменяют только знак, т. е. f(-x)=-f(x).

График четной функции симметричен относительно оси ординат, не четной функции симметричен относительно начала координат.

Функция f(х) называется периодической, если существует такое число l≠0 (называемое пе­риодом), что в каждой точке области определения функ­ции f(х) выполняется условие f(х+l) = f(х).

Пусть функция у=f(х) определена на отрезке [а, b] и является монотонной, а область изменения функции у есть отрезок [α, β]. Каждому значе­нию у_о из отрезка [α, β] будет соответствовать одно значе­ние х₀ из отрезка [а, b] такое, что у_о=f(х_о). Следователь­но, на отрезке [α, β] определена функция х=j(у). Эта функция х=j(у) называется обратной для функции у=f(х) и, наоборот, функция y= f(х) является обратной для функ­ции х=j(у). Поэтому их называют взаимно обратными.

Графиками функций у=f(х) и х=j(у) служит одна и та же линия, так как эти функции выражают одну и ту же функцио­нальную зависимость между переменными х и у.

Примерами взаимно обратных функций являются функции у=ах+b и х= , где а≠0, или функции у=а^x и х=log_ау, где а>0, а≠1.

Построение их графиков отличается лишь тем, что значения независимой переменной для функции у=f(х) откладывают на горизонтальной оси Ох, а для функции х=j(у) — на вертикаль­ной оси Оу.

Чтобы избежать это­го неудобства, в уравнении x=j(у) переставим переменные. Полученная функция у=j(х) так­же называется обратной для функции y=f(х).

Пусть у является функцией перемен­ной и, а переменная и, в свою очередь, является функцией от переменной х, т. е. у=f(и) и и=j(х). Тогда функция у=f(j(х)) называется функцией от функции (или сложной функцией), если область определения функции f содержит множество значений функции j. Переменная и в этом слу­чае называется промежуточной переменной.

Графики функций

Графиком функции f называется множество всех точек (x;y) координатной плоскости, где y=f(x), а x проходит всю область определения функции f.

Подмножество координатной плоскости является графиком какой – либо функции, если оно имеет не более одной общей точки с любой прямой параллельной оси O,Y

не функция функция