1.1. Топологические пространства. Сходимость и понятие предела в топологических пространствах. Непрерывные отображения. Аналоги топологических понятий в конечномерных пространствах: открытое множество, окрестность, сходимость, непрерывность. Необходимое и достаточное условие непрерывности (формулировка теоремы).
1.2. Линейные пространства. Линейные операторы. Ядро оператора. Необходимые и достаточные условия взаимнооднозначности линейного оператора. Линейные топологические пространства. Локальная выпуклость.
1.3. Нормированные и банаховы пространства. Примеры. Пространства 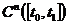 и
и 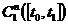 Пространства со скалярным произведением. Гильбертовы пространства.
Пространства со скалярным произведением. Гильбертовы пространства.
1.4. Взаимосвязи основных структур в различных видах функциональных пространств (структурная схема).
1.5. Линейные непрерывные функционалы в линейных топологических пространствах. Сопряженные пространства. Сильная топология в сопряженных пространствах. Сопряженные операторы. Оператор, сопряженный к линейному оператору 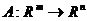 в евклидовых пространствах Rm, Rn (утверждение и доказательство).
в евклидовых пространствах Rm, Rn (утверждение и доказательство).
1.6. Пространство, сопряженное к конечномерному линейному пространству. Общий вид линейного непрерывного функционала в конечномерном линейном пространстве. Пространство, сопряженное к гильбертову пространству. Теорема Ф.Рисса о структуре линейного непрерывного функционала в гильбертовом пространстве (без доказательства).
1.7. Сильное дифференцирование в банаховых пространствах. Определение сильной производной. Производная Фреше в конечномерных пространствах. Дифференциал Фреше. Условие регулярности отображения. Понятие гладкости (непрерывный дифференцируемости).
1.8. Теорема о дифференцируемости сложной функции для сильной производной (формулировка и примеры решения).
1.9. Слабое дифференцирование в линейных топологических пространствах. Первая вариация по Лагранжу. Производная Гато. Соотношение между дифференцируемостью по Гато, непрерывностью отображения и дифференцируемостью по Фреше.
1.10. Связь между сильной и слабой дифференцируемостью. Достаточные условия
дифференцируемости по Фреше (без доказательства).
1.11. Старшие сильные производные. Два подхода к определению производных высших
порядков. Определения второй производной на основе первого и второго подходов. Вторая производная как производная отображения, определяемого первой производной. Вторая производная, задаваемая при помощи разложения приращения отображения. Значение вторых производных в конечномерных пространствах. Формула Тейлора.
1.12. Дифференцируемость конкретных функционалов и отображений:
1) производные Фреше билинейной и квадратичной формы, скалярного произведения и нормы в гильбертовом пространстве;
2) производная Фреше отображения
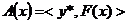 ,
, 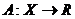 , где
, где  ,
,  , X и Y – банаховы;
, X и Y – банаховы;
3) 
Определяемого соотношением
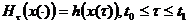 , где
, где 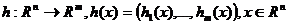
4) производная Фреше отображения
 ,
,
где 
5) производная Фреше функционала  , определяемого соотношением
, определяемого соотношением 

1.13. Теорема Люстерника (общая формулировка). Геометрический смысл теоремы.