Основы начертательной геометрии

И.В. САБАЕВ, Г.Н. ЕГОРОВА

О С Н О В ЫИ Т И П О В ЫЕ З А Д А Ч И

Н А Ч Е Р Т А Т Е Л Ь Н О Й Г Е О М Е Т Р И И

УЧЕБНОЕ ПОСОБИЕ

ВОРОНЕЖ

ОГЛАВЛЕНИЕ

Предисловие ………………………………………………………………...

Введение …………………………………………………………………….

Основы начертательной геометрии

Лекция 1. Сущность метода проецирования………………………………

Лекция 2. Ортогональная система двух плоскостей проекций…………...

Лекция 3. Прямая ……………………………………………………………

Лекция 4. Определение натуральной величины отрезка прямой и углов наклона его к плоскостям проекций……………………………

Лекция 5. Плоскость…………………………………………………………

Лекция 6. Главные линии плоскости……………………………………….

Лекция 7. Параллельность и перпендикулярность прямых и плоскостей..

Лекция 8. Пересечение прямой с плоскостью………………………………

Лекция 9, 10. Многогранники. Кривые линии и поверхности. Пересечение

поверхностей плоскостью.Развертки поверхностей……………

Лекция 11. Пересечение прямой с геометрическими поверхностями.

Взаимное пересечение гранных поверхностей…………………

Лекция 12. Пересечение поверхностей вращения…………………………..

Лекция 13,14. Изображение геометрических тел с вырезами………………

Лекция 15,16. Аксонометрические поверхности…………………………….

ПРЕДИСЛОВИЕ

Изучение начертательной геометрии является важнейшей частью инженерной подготовки специалистов в области машиностроения.

В основу учебного пособия положен курс лекций, который на протяжении ряда лет читается на кафедре начертательной геометрии и инженерной графики.

Главная цель данного учебного пособия заключается в изложении материала в доступной форме и доходчивом раскрытии смысла и цели начертательной геометрии. Терминология, буквенные обозначения приведены в соответствии с требованиями государственных стандартов.

Работа с данным материалом предполагает выявление большей самостоятельности студентов при выполнении домашних заданий.

Представленные во второй части пособия задачи позволяют наиболее полно развить пространственное воображение студентов с последующим использованием при выполнении технических чертежей, обеспечивая их выразительность и точность.

Материал пособия размещен в последовательности, соответствующей порядку работы студента при изучении курса начертательной геометрии и полностью отвечает последним требованиям ГОСа.

ВВЕДЕНИЕ

Предметом начертательной геометрии является изложение и обоснование способов построения изображений пространственных форм на плоскости и способов решения задач геометрического характера по заданным изображениям этих форм. Начертательная геометрия со времен ее основоположника Г. Монжа (1748 – 1818) завоевала себе достойное место в высшей школе, как наука, без которой немыслимо образование по специальностям инженерного профиля.

Важное прикладное значение этой дисциплины состоит в том, что она учит грамотно владеть выразительным техническим языком – языком чертежа, создавать чертежи и свободно читать их, а также способствует развитию пространственного воображения и навыков логического мышления.

Учебное пособие «Основы и типовые задачи начертательной геометрии» состоит из краткого лекционного курса и задач для закрепления теоретических знаний по начертательной геометрии и инженерной графики. Оно может быть полезным и для студентов, обучающихся по технологическим специальностям университета.

Опыт работы со студентами вуза показывает, что многие из них при изучении предмета «Инженерная графика» преодолевают значительные трудности, овладевая разделом «Элементы начертательной геометрии», недостаточно ясно представляя себе пространственные операции, выполняемые на эпюре.

Предлагаемые задачи тесно увязаны с лекциями и рабочей программой курса. Задания расположены в логической связи, способствующей успешному усвоению курса при условии их последовательного решения.

Данное пособие в отдельных вариантах прошло апробацию временем, поэтому авторы надеются, что оно и в предложенном комплексе принесет положительные результаты.

Задач решаются по разделам после каждой лекции. Предполагается их тщательное графическое исполнение карандашом или тонким фломастером в простом и цветном вариантах с использованием знаний по геометрическому черчению (шрифты, типы линий). Необходимо соблюдать большую точность исполнения, не забывая и эстетическую сторону оформления.

Задачи решаются в строгой последовательности, т.к. каждая последующая задача включает элементы предыдущей. Исключается выполнение решений «от руки»: только с помощью циркуля (эллипс-овал) или лекала (гипербола, парабола).

При решении задач важно избегать «соблазна» их механического копирования, что на 100 % ведет к полному отрицательному результату при получении зачета и сдаче экзамена.

В определенных случаях (при высоком рейтинге) кафедра начертательной геометрии и инженерной графики освобождает студента от сдачи экзамена, выставляя заранее положительную оценку (4 или 5) в зависимости от рейтинга. Остальные студенты сдают экзамен по начертательной геометрии во время сессии.

Лекция 1.СУЩНОСТЬ МЕТОДА ПРОЕЦИРОВАНИЯ

Построение изображений в курсе начертательной геометрии основаны на методе проекций.

1.1. Центральная проекция 1. 2. Параллельная проекция

(перспектива)

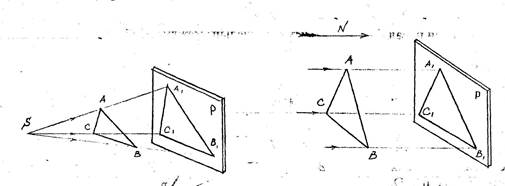
S- центр проекции. Центр проекции S удален в

P- плоскость проекций. бесконечность и все лучи

A₁- проекция точки A. как пересекающиеся в бес-

SA- проецирующая прямая конечно удаленной точке

в пересечении с плоскостью будут параллельны некото-

проекций даст точку А₁. рому направлению.

Так как каждая геометри-

ческая фигура есть совокуп-

ность точек, то и проекция

фигуры есть совокупность

проекции всех ее точек.

1.2.1.Свойства параллельной проекции

1. Проекцией точки является точка.

2. Проекцией прямой линии является прямая.

3. Если точка лежит на прямой, то проекция точки принадлежит проекции этой прямой.

4. Если прямая параллельна направлению проецирования, то она спроецируется в точку.

5. Отрезок прямой, параллельный плоскости проекции, проецируется на плоскость в натуральную величину.

AB // пл. P

A₁В₁= AB как параллельные

отрезки между параллельными прямыми.

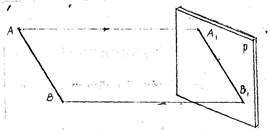
6. Проекции параллельных прямых параллельны между собой.

A₁B₁// C₁D₁

AB // CD.

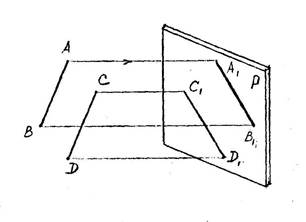Если предположить, что A₁B₁ и C₁D₁ пересекаются, то точка пересечения была бы в пересечении самих прямых AB и CD, но это противоречит условию, что AB параллельна CD.

7. Отношение отрезков прямой равно отношению их проекций.

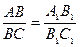; так как AA₁//BB₁//CC₁ (деление отрезка на равные части).

Середина отрезка проецируется в середину проекции отрезка.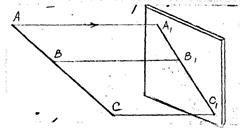

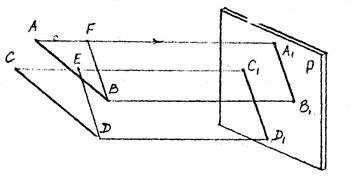
8. Отношение отрезков двух параллельных прямых равно отношению их

проекций.

AB//CD. Проведем вспомогательные линии FB//A₁B₁ и ED//С₁D₁.

Из подобия треугольников AFB и CED как треугольников с параллельными сторонами имеем:

AB ₌ FB _; AB ₌ A₁B₁

CD ED CD C₁D₁

1.3. Ортогональная проекция

Еще большее упрощение дает применение ортогонального проецирования, когда направление проецирования перпендикулярно плоскости проекции. В этом случае нетрудно установить соотношение между длиной натурального отрезка и длиной его проекции.

Если AB образует с плоскостью проекции угол a, то 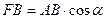, но FB параллельна и равна A₁В₁, следовательно, .

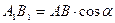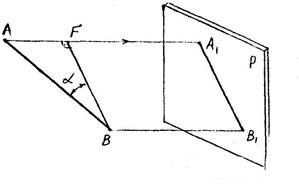
Рассмотренные методы проецирования позволяют однозначно решать прямую задачу, т.е. по оригиналу строить чертеж, но обратная задача - воспроизведение по чертежу оригинала не решается, т.е. рассмотренные методы не обладают свойством обратимости. Поэтому воспользуемся некоторыми дополнениями к ортогональному проецированию и разберем так называемый комплексный чертеж.

Лекция 2.ОРТОГОНАЛЬНАЯ СИСТЕМА ДВУХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Две взаимно перпендикулярные плоскости проекции горизонтальная – П₁ и фронтальная - П₂, пересекаясь, образуют ось ОХ и делят пространство на четыре четверти I,II,III,IV. Плоскости не прозрачны и бесконечны. Наблюдатель находится в I четверти. Спроецируем на плоскости проекции какую- либо точку A и получим две ее проекции: горизонтальную - A₁ и фронтальную A₂. Условимся в дальнейшем точки в пространстве обозначать заглавными буквами латинского алфавита: A, B, C,…, а их проекции теми же буквами с индексами A₁, B₁, C₁,…- горизонтальные и A₂, B₂, C₂,…- фронтальные.

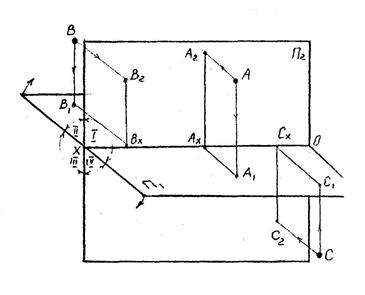
Такая система является обратимой, т.к. восставив перпендикуляры из точек A₁ и A₂ – в пересечении получим точку A. Для получения плоского чертежа совмещаем плоскость П₁ с П₂, вращая ее вокруг оси ОХ. Такой чертеж и называется комплексным чертежом или эпюром.

Точка A лежит в I четверти пространства.

А₂А₁- линия связи,

А₂А_х- высота точки,

А₁А_х- глубина точки.

Горизонтальная и фронтальная проекции точки лежат на одном перпендикуляре к оси проекции ОХ.

Для примера: точка B лежит во II четверти пространства на одинаковом расстоянии от плоскостей проекции, точка С лежит в IV четверти пространства.

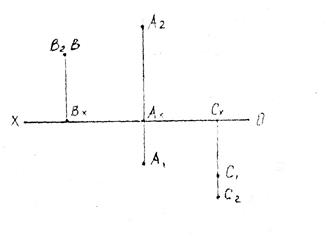
2.1. Ортогональная система трех плоскостей проекции.

Прямоугольная система координат в пространстве

Комплексный чертеж, состоящий из ортогональных проекций, является

обратимым чертежом. Однако реконструкция оригинала, у которого имеются

профильные элементы, становится проще, если имеется еще одна проекция на третью плоскость. Назовем ее профильной плоскостью проекции - П₃ и

проекции точек на нее A₃, B₃, C₃,…

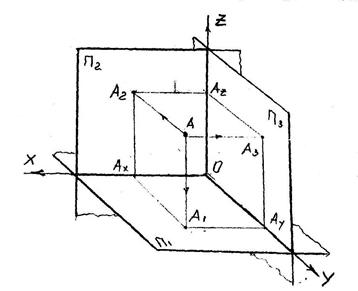
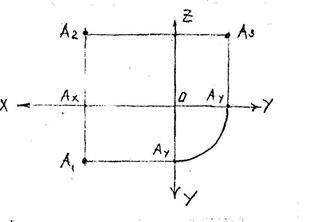
Три координатные плоскости делят пространство на 8 октантов. У первого

октанта все три координатные оси имеют положительные направления.

ОА_х - абсцисса точки - широта.

ОА_у - ордината точки - глубина.

ОА_z - аппликата точки - высота.

Точка задается координатами

А (х, у, z). Фронтальная и профильная проекции точки лежат на одном перпендикуляре к оси проекции OZ.

Лекция 3.ПРЯМАЯ

3.1.Положение прямой относительно плоскостей проекций

Прямая общего положения - не параллельна и не перпендикулярна ни одной из плоскостей проекции.

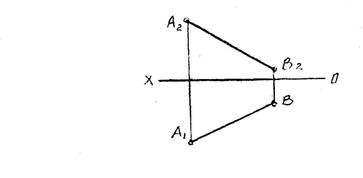
Проецирующие прямые – перпендикулярные к какой-либо плоскости проекции и проецирующиеся на нее в точку.

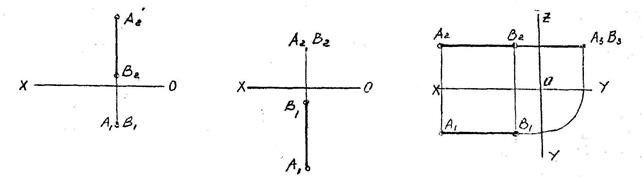
а) Горизонтально- б) Фронтально- в) Профильно-

проецирующая проецирующая проецирующая

прямая (^ пл. П₁) прямая (^ пл. П₂) прямая (^пл. П₃)

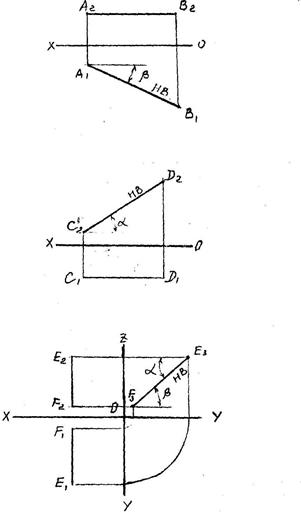
Прямые уровня – параллельные какой-либо плоскости проекции и

проецирующиеся на нее в натуральную величину.

а) Горизонтальная прямая (горизонталь) - прямая параллельна плоскости П₁. Фронтальная проекция прямой всегда параллельна оси ОХ. β - угол наклона прямой к плоскости П₂. A₁B₁- натуральная величина (НВ). б) Фронтальная прямая (фронталь) – прямая параллельна плоскости П₂. Горизонтальная проекция прямой всегда параллельна оси ОХ. α - угол наклона прямой к плоскости П₁. C₂D₂- натуральная величина (НВ). в) Профильная прямая – прямая параллельна плоскости П₃. FE- натуральная величина.

Положение прямой в пространстве вполне определяется двумя ее проекциями.

3.2.Способы преобразования чертежа

Решение метрических задач, связанных с определением истинных размеров изображенных на эпюре фигур и тел, может встретить значительные трудности, если заданные проекции не подвергать специальным преобразованиям. Преобразования осуществляются с помощью способов вращения и перемены плоскостей проекций.

3.2.1.Способ вращения

При этом способе преобразования плоскости проекции остаются в неизменном виде, а сама геометрическая фигура вращается до нового положения, удобного для решения задачи.

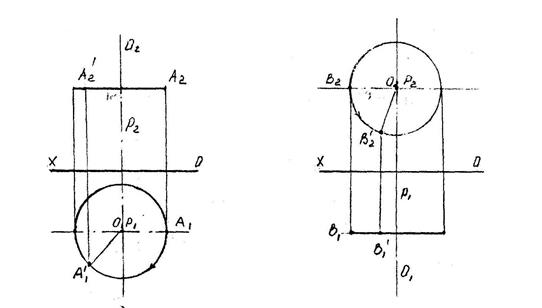
Преобразование точки

При вращении точки вокруг оси, перпендикулярной какой-либо плоскости проекции, одна из проекций точки перемещается по окружности, а другая по прямой, параллельной оси ОХ.

3.2.2.Способ перемены плоскостей проекций

Сущность этого способа заключается в том, что положение фигуры в пространстве остается неизменным, а система плоскостей проекций замещается новой системой двух взаимно перпендикулярных плоскостей. Новая система выбирается так, чтобы получить положение, удобное для решения задачи.

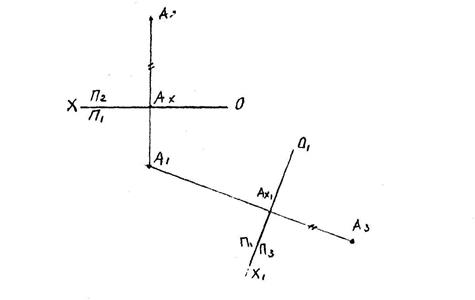
Преобразование точки

В системе плоскостей проекции 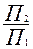дана точка А. Заменим, например, плоскость П₂ новой плоскостью П₃, перпендикулярной плоскости П₁. Затем плоскость П₃ совмещается с плоскостью П₁.

В новой системе 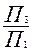расстояние А₃Ах₁=А₂Ах.

Лекция 4.ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫОТРЕЗКА ПРЯМОЙ И УГЛОВ НАКЛОНА ЕГО К ПЛОСКОСТЯМ ПРОЕКЦИЙ

Дана прямая АВ. Определить ее натуральную величину и углы наклона к плоскостям проекций П₂ и П₁.

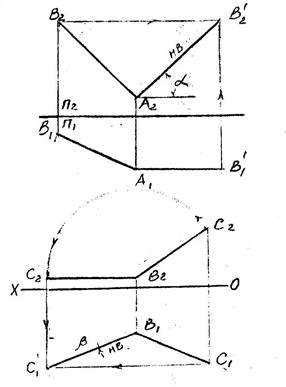
4.1.Способ вращения

Повернув отрезок прямой до положения параллельного какой-либо плоскости проекций можно легко определить его натуральную величину и угол наклона к другой плоскости проекций. Траектория движения одной из точек будет проецироваться на одну из плоскостей в виде дуги окружности, а на другую в виде прямой параллельной оси ОХ.

Пример 1.

В нашем случае отрезок АВ вращаем до положения параллельного плоскости П₂, на которую он и спроецируется в натуральную величину (отрезок А₂В₂). Получим угол a, угол наклона отрезка АВ к пл. П₁.

Пример 2.

Отрезок ВС вращаем до положения параллельного плоскости П₁ на которую он и спроецируется в натуральную величину.

β - угол наклона прямой к плоскости П₂.

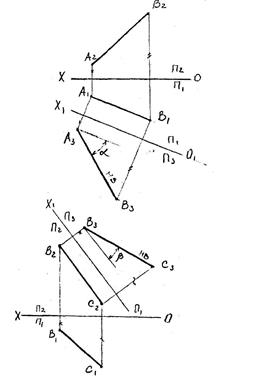
4.2.Способ перемены плоскостей проекций

Прямая общего положения АВ дана в системе плоскостей проекций .

Заменим, например, плоскости проекций таким образом, чтобы одна из них была параллельна этой прямой. На эту плоскость прямая и спроецируется в натуральную величину.

Пример3. В нашем случае плоскость П₂ заменена на плоскость П₃, параллельную прямой АВ (на эпюре параллельна проекции А₁В₁). На эту плоскость прямая и спроецируется в натуральную величину, α - угол наклона прямой АВ к плоскости П₁ (прямая А₃В₃). Пример 4. Определить натуральную величину отрезка ВС и угол наклона его, к плоскости П₂. В этом случае заменяем плоскость П₁ на П₃, параллельную прямой ВС (на эпюре В₂С₂), на которой и имеем натуральную величину отрезка В₃С₃ и угол наклона его к плоскости П₂(угол b). Для решения некоторых метрических задач требуется провести ряд преобразований, при которых прямая спроецируется в точку. Пример 5. Спроецировать в точку горизонтальную прямую АВ. В этом случае достаточно одной перемены плоскостей проекций. Пример 6. Спроецировать в точку прямую общего положения ВС. В этом слуае для достижения результата требуется двойная замена плоскости проекций.

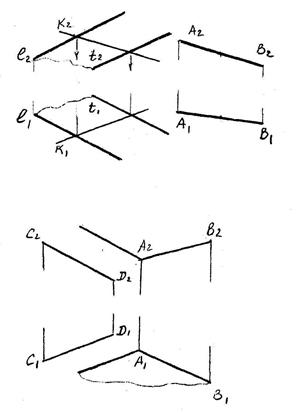
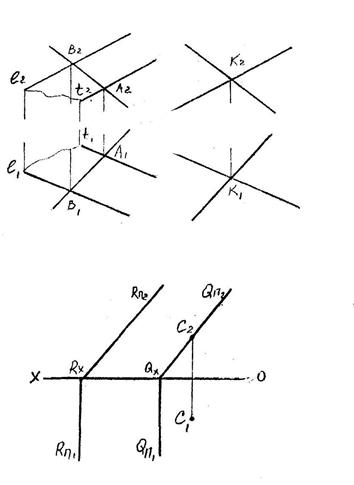
4.3.Взаимное расположение двух прямых

Две прямые в пространстве могут пересекаться, быть параллельными или скрещиваться.

Пересекающиеся прямые

Если прямые пересекаются, то точки пересечения их одноименных проекций лежат на одном перпендикуляре к оси проекций (К₂К₁).

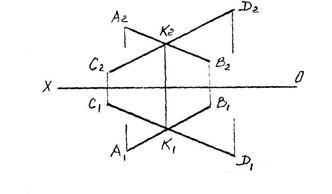
Параллельные прямые

Из свойств параллельного проецирования известно, что проекции параллельных прямых параллельны. И если АВ параллельна CD, то А₂В₂ параллельна С₂D₂ и А₁В₁ параллельна С₁D₁. Но если эти прямые являются профильными, то для оценки их взаимного расположения следует воспользоваться профильной плоскостью проекции.

В общем случае справедливо и обратное утверждение: если на эпюре одноименные проекции прямых параллельны, то и прямые в пространстве – параллельны.

Скрещивающиеся прямые

Если прямые не пересекаются и не параллельны, то они скрещивающиеся и точки пересечения их одноименных проекций не лежат на одном перпендикуляре к оси проекций. В определении видимости помогут так называемые конкурирующие точки (1-4).

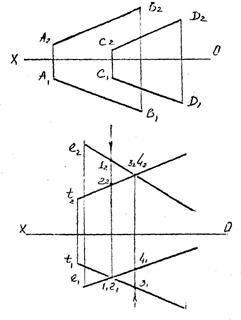
4.4.Ортогональная проекция прямого угла

Прямой угол проецируется без искажения, если хотя бы одна его сторона параллельна какой-либо плоскости проекций.

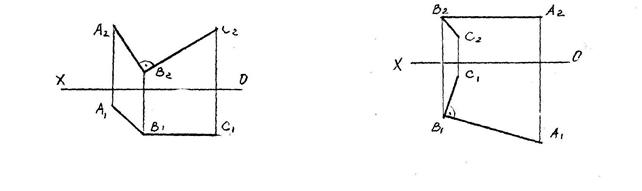
Лекция 5.П Л О С К О С Т Ь (

В пространстве плоскость может быть определена следующими способами:

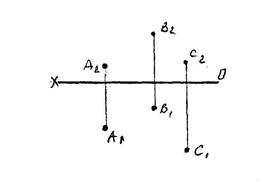
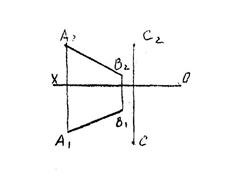
1. Тремя точками, не лежащим 2. Прямой и точкой вне ее.

на одной прямой.

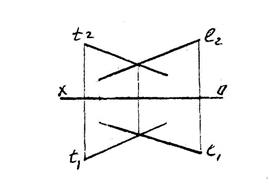
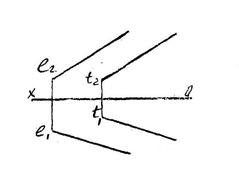
3. Двумя пересекающимися 4. Двумя параллельными

прямыми. прямыми.

5.1.Положение плоскости относительно плоскостей проекций

Плоскость общего положения – не параллельна и не перпендикулярна ни одной из плоскостей проекций. Обычно обозначаются на эпюре вышеперечисленными чертежами.

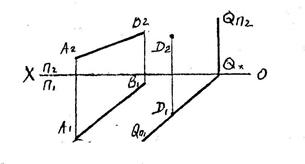
Проецирующие плоскости – перпендикулярные одной из плоскостей проекций и проецирующиеся на нее в прямую линию. О положении таких плоскостей в пространстве очень удобно судить по их следам, т. е. линиям, по которым данная плоскость пересекается с плоскостями проекций. На эпюре такая плоскость обозначается обычно одним или двумя следами.

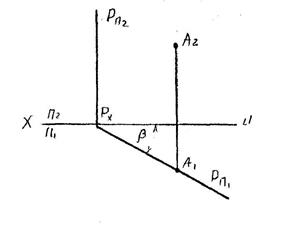
а) Горизонтально - проецирующая

плоскость - перпендикулярная

плоскости П₁ и проецирующаяся

на нее в прямую (след Рп₁),

фронтальный след (Рп₂) перпен-

дикулярен оси ОХ, β – угол нак-

лона ее к плоскости П₂. На чер-

теже обычно обозначается одним следом (проецирующим).

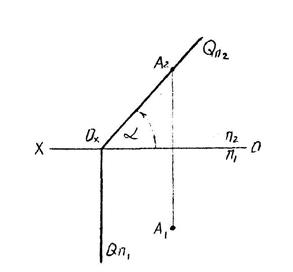
б) Фронтально - проецирующая

плоскость- перпендикулярная

плоскости П₂ и проецирующаяся

на нее в прямую (след Qп₂).

Горизонтальный след (Qп₁)

перпендикулярен оси ОХ.

a - угол наклона к плоскости

П₁. На чертеже обыч-

но обозначается одним

следом (проецирующим).

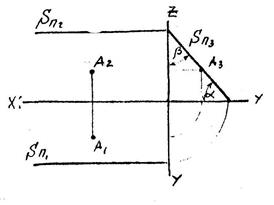
в) Профильно-проецирующая

плоскость - перпендикулярная

плоскости П₃ и проецирующаяся

на нее в прямую (след Sп₃).

Горизонтальный и фронтальный

следы плоскости (Sп₁ и Sп₂)

параллельны оси ОХ. На черте-

же обычно обозначаются двумя

следами - фронтальным и гори-

зонтальным или одним профиль-

ным (проецирующим).

Плоскости уровня – параллельные одной из плоскостей проекций.

Горизонтальная (R). Фронтальная (Q). Профильная (T).

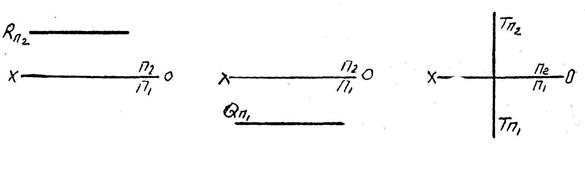
5.2.Прямая и точка в плоскости

1) Прямая принадлежит

плоскости, если она имеет

с ней две общие точки.

2) Точка лежит в плоскости,

если она лежит на прямой,

принадлежащей этой плос-

кости.

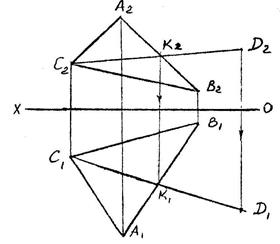
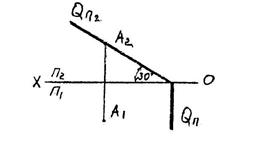
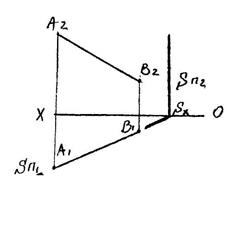
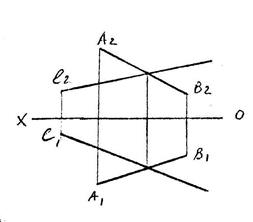
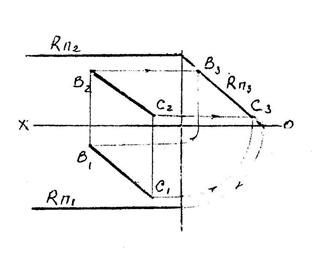
Пример 1. Лежит ли точка F в плос- кости, заданной параллель- ными прямыми? С помощью прямой К, при- надлежащей плоскости, убеждаемся в том, что точка F в плоскости не лежит. Пример 2. Через точку А провести фронтально-проецирующую плоскость Q под углом 30^о к плоскости проекций П₁. Пример 3. Прямую АВ заключить в го- ризонтально-проецирующую плоскость S. Пример 4. Через прямую АВ провести плоскость общего положе- ния. Задача имеет мно- жество решений, т.к. через прямую можно провести бесчисленное количество плоскостей. Одно из реше- ний - задать плоскость пересекающимися прямыми. Пример 5. Прямую ВС заключить в профильно-проецирующую плоскость R. Для решения находим про- фильную проекцию прямой, через которую и пройдет проецирующий след плос- кости Rп₃. Остальные следы такой плоскости займут положение, парал- лельное оси ОХ.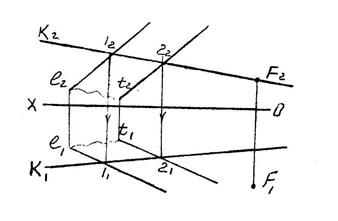

Лекция 6. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ

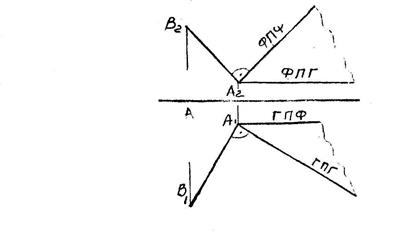
К числу прямых, занимающих особое положение в плоскости, отнесем горизонтали, фронтали и линии наибольшего наклона к плоскостям проекций.

Горизонтали плоскости -

прямые лежащие в плоскости

и параллельные плоскости П₁.

Фронтальная проекция гори-

зонтали (ФПГ) параллельна

оси ОХ.

Фронтали плоскости –

прямые, лежащие в плоскости

и параллельные плоскости П₂.

Горизонтальная проекция фрон-

тали (ГПФ) параллельна оси ОХ.

В любой плоскости можно про-

вести бесчисленное множество

горизонталей и фронталей.

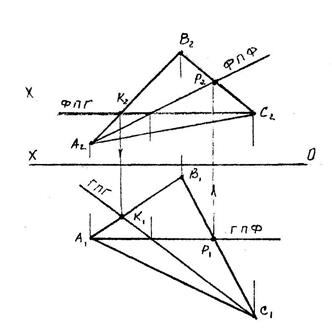
Пример 1. Пример 2.

В плоскости, заданной па- В плоскости Q через точку А

раллельными прямыми, про- провести фронталь.

вести фронталь, отстоящую

от плоскости П₂ на 20 мм.

Линии наибольшего ската

плоскости – прямые перпен-

дикулярные горизонталям и

образующие наибольший

угол с горизонтальной плос-

костью проекций. По прави-

лам проецирования прямого

угла горизонтальная проекция

линии наибольшего ската пер-

пендикулярна к ГПГ. Фрон-

тальная проекция определя-

ется как недостающая.

Линия наибольшего ската

может служить для опре-

деления угла наклона плос-

кости к плоскости проекций П₁.

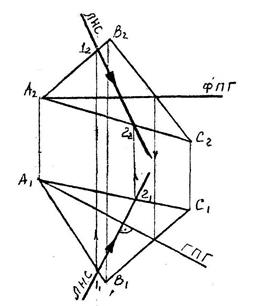
6.1.Определение натуральной величины плоской фигуры

способом вращения (а) и способом перемены плоскостей проекций (б)

Решение задачи покажем на примерах.

Дан треугольник АВС. Требуется определить его натуральную величину и угол наклона (a) к плоскости П₁.

1. Проводим горизонталь плоскости.

2. Проецируем ее в точку:

а) При способе вращения поворачивая ее до положения, перпендикулярного плоскости П₂^..

б) При способе перемены плоскостей проекций подводя под нее новую плоскость П₃.

В этих случаях и плоская фигура спроецируется на плоскость проекций в прямую, где и определяется угол a.

3. Производим еще некоторые преобразования при которых фигура располагается параллельно одной из плоскостей проекций и спроецируется на нее в натуральную величину.

Способ вращения (а)

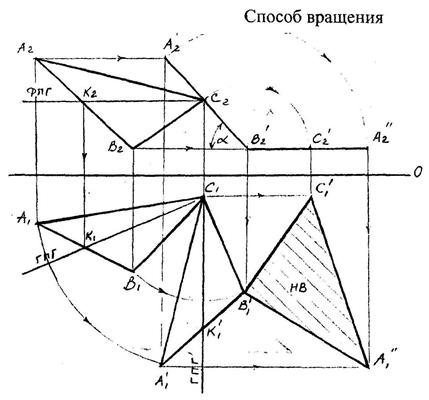
а) Решая задачу

способом враще-

ния, повернем

плоскую фигуру

до положения,

параллельного

плоскости проек-

ций П_1, на кото-

рую она и спрое-

цируется в на-туральную вели-

чину.

Способ перемены плоскостей проекций (б)

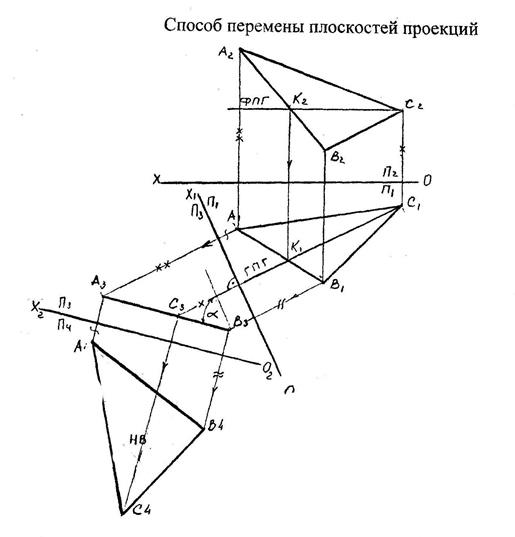
б) Решая задачу способом перемены плоскостей проекций

подведем новую плоскость П₄ под плоскость треугольника, на которую он и спроецируется в натуральную величину.

Лекция 7. ПАРАЛЛЕЛЬНОСТЬ И ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ
И ПЛОСКОСТЕЙ

7.1.Параллельность прямой и плоскости

Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости. Если для решения задач не требуется показа оси ОХ, она не проводится. Пример 1. Через точку провести прямую Е, параллельную плоскости ВСА. (В решении – бесконечное множество прямых.) В нашем примере прямая Е // АС. Пример 2.

Параллельна ли прямая АВ плоскости, заданной прямыми? (Не параллельна, т. к. А₁В₁ не параллельна соответствующей проекции прямой К, расположенной в данной плоскости.)

Пример 3.

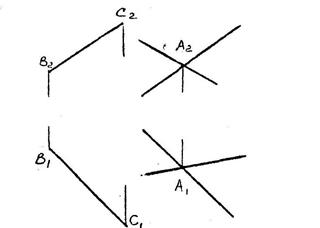
Через прямую АВ провести плоскость, параллельную прямой СD.

Для решения достаточно через точку А провести прямую, параллельную СD.

Пример 4.

Через точку А провести

Плоскость, параллельную

прямой ВС (бесконечное

множество плоскостей).

Для решения задачи про-

ведем через точку А две

пересекающиеся прямые

(плоскость), одна из кото-

рых параллельна прямой

ВС.

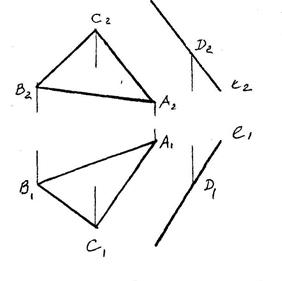
Пример 5.

Через точку D провести

горизонтально-проецирую-

щую плоскость Q парал-

лельно прямой АВ.

7.2.Параллельность плоскостей

Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то такие плоскости взаимно параллельны. Если плоскости выражены следами, то их одноименные следы параллельны.

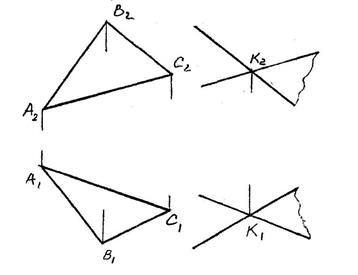
Пример 1.

Через точку К провести

плоскость, параллельную

плоскости треугольника

АВС, задав ее двумя пере-

секающимися прямыми.

Эти прямые будут взаимно

параллельны любым двум

прямым треугольника АВС.

Пример 2.

Через точку К провести

плоскость, параллельную

плоскости, заданной парал-

лельными прямыми, также

задав ее двумя пересекаю-

щимися прямыми.

Для решения введем в за-

данную плоскость любую

прямую (АВ), а затем ре-

шим как предыдущую

задачу.

Пример 3.

Через точку С провести

плоскость Q, параллельную

заданной плоскости R.

7.3.Перпендикулярность прямой и плоскости

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. Если прямая перпендикулярна плоскости, то проекции этой прямой перпендикулярны к соответствующим проекциям горизонталей и фронталей (как проекции прямого угла).

А₁В₁ 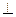ГПГ.

А₂В₂ 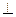ФПФ.

Пример 1. Пример 2.

Через точку А провести Через точку С провести плос-

перпендикуляр к плоскости кость, перпендикулярную

треугольника ВСD. прямой АВ. Плоскость за-

Задачу помогут решить дать горизонталью и фрон-

горизонталь и фронталь талью.

плоскости, введенные в

треугольник BCD.

7.4.Взаимно перпендикулярные плоскости

Плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Пример.

Через точку D провести

плоскость, перпендику-

лярную к плоскости треу-

гольника АВС.

Решение.

Проводим главные

линии плоскости.

Проводим перпен-

дикуляр к плоскос-

ти.

Вводим любую пря-

мую Т, т.к. через

этот перпендикуляр

можно провести мно-

жество плоскостей,

перпендикулярных

плоскости треуголь-

ника АВС.

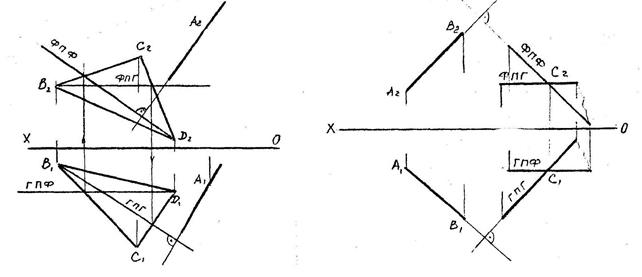
Лекция 8. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ

8.1.Пересечение двух плоскостей

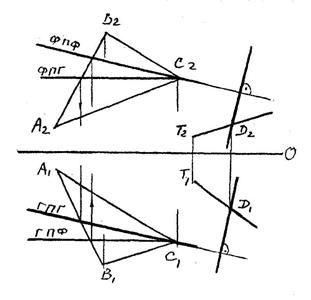
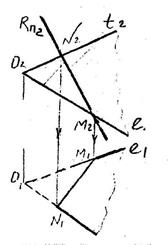
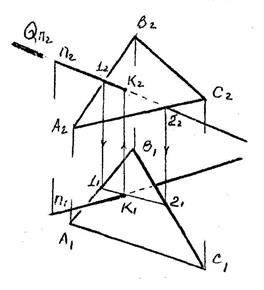
1. Встреча прямой с проеци- рующей плоскостью. Точка встречи К лежит на проеци- рующем следе плоскости. 2. Пересечение плоскости общего положения с проеци- рующей плоскостью R. Определяем точки встречи каждой из прямых Т и Е с плоскостью (линия NM). 3. Встреча прямой с плоскостью общего положения. Для определения точки встречи прямой с плоскостью следует: Провести через прямую вспомогательную прое- цирующую плоскость (в нашем случае фрон- тально- проецирующую плоскость Q); Найти вспомогательную линию пересечения этой плоскости с задан- ной плоскостью (Линия 1-2);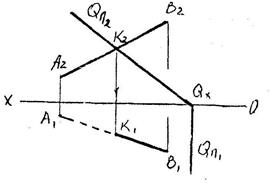

Точка встречи вспомогательной линии пересечения с данной

прямой и будет искомой (точка К).

Видимость определяется с помощью конкурирующих точек (см. лекцию 4).

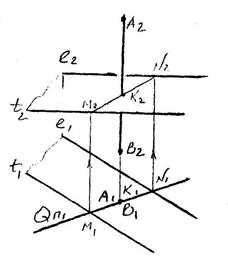
Пример1.

Определить точку встречи прямой

АВ с плоскостью заданной прямыми

(Е,Т).

Для решения заключаем прямую в

горизонтально- проецирующую плос-

кость Q, находим линию пересечения

плоскостей MN, а затем и точку К.

8.2.Пересечение плоскостей общего положения

Даны две плоскости общего положения, заданные треугольником и

параллельными прямыми.

Для решения задачи вводим две вспомогательные проецирующие

плоскости (в нашем случае плоскость Q и плоскость R), находим

их линии пересечения с каждой из плоскостей; дальнейшее решение

ясно из рисунка.

Лекции 9,10.МНОГОГРАННИКИ. КРИВЫЕ ЛИНИИ И ПОВЕРХНОСТИ. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ПЛОСКОСТЬЮ.

РАЗВЕРТКИ ПОВЕРХНОСТЕЙ

Краткость предлагаемого курса лекций не предполагает подробного

изложения материала по этому вопросу.

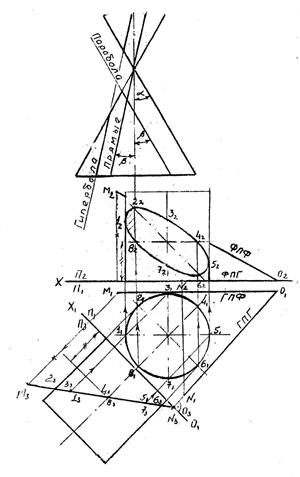
9.1.Пересечение гранных поверхностей проецирующими плоскостями

Для определения фигуры сечения, достаточно найти точки пересечения ребер и граней тела с данной плоскостью. Из чертежа видны все построения точек сечения пирамиды проецирующей плоскостью, определение натуральной величины фигуры сечения и ребер пирамиды для построения развертки.

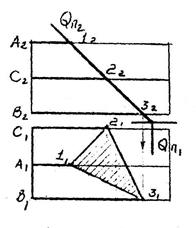
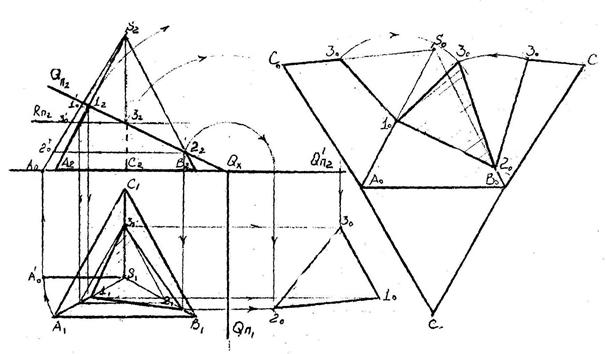
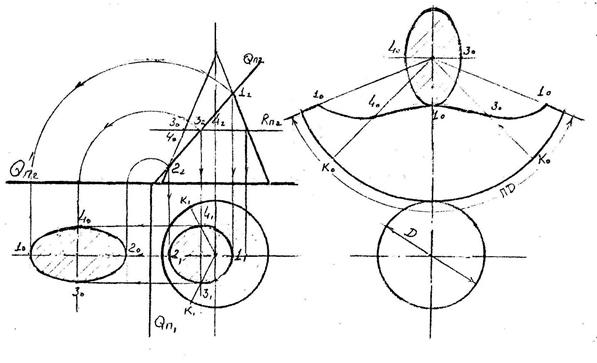
9.2.Пересечение тел вращения проецирующей плоскостью

Пересечение цилиндрической поверхности плоскостью

На чертеже показано построение сечения, определение натуральной величины эллипса и развертки усеченной части цилиндра.

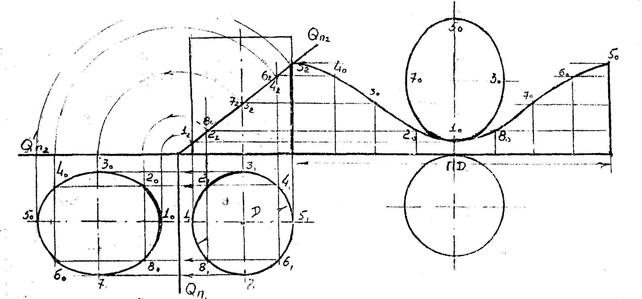
Пересечение конической поверхности плоскостью.Построение развертки

Для получения сечения большую ось эллипса 1-2 делим пополам, проводим через эту точку вспомогательную секущую плоскость и находим положение малой оси эллипса 3-4.

Дальнейшее построение натуральной величины сечения и развертки усеченной части ясно из чертежа.

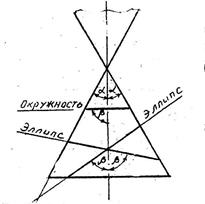
9.3.Кривые второго порядка

Рассмотрим так называемые конические сечения –кривые второго порядка (окружность, эллипс, парабола и гипербола), широко применяемые в науке и технике.

Без доказательств приводим чертежи и следующие положения:

1. Если пересечь прямой круговой конус плоскостью, параллельной его основанию, – в сечении получим окружность (b = 90⁰).

2. Если пересечь конус плоскостью, не параллельной ни одной из его образующих – в сечении получим эллипс (b > a).

3. Если пересечь конус плоскостью, параллельной одной из его образующих, – в сечении получим параболу (b = a).

4. Если пересечь конус плоскостью,параллельной двум его образующим (в частном cлучае параллельно его оси),– в сечении получим гиперболу (b< a).

При пересечении тел плоскостями общего положения решение намного упрощается, если путем преобразования чертежа перейти к новому изображению, когда плоскость становится проецирующей.

Лекция 11.ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ГЕОМЕТРИЧЕСКИМИ ПОВЕРХНО-

СТЯМИ.ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ГРАННЫХ ПОВЕРХНОСТЕЙ

Для построения точек пересечения прямой с какой–либо поверхностью следует:

1. провести через прямую вспомогательную (проецирующую) плоскость;

2. найти сечение поверхности плоскостью;

3. определить точки пересечения прямой с контуром сечения (точки входа и выхода);

4. определить видимость прямой.

Поделиться:

Поиск по сайту

©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2021-04-15 Нарушение авторских прав и Нарушение персональных данных

Поиск по сайту:

Читайте также:

Деталирование сборочного чертежа

Когда производственнику особенно важно наличие гибких производственных мощностей?

Собственные движения и пространственные скорости звезд

Тема 11. Банковские риски и способы их оценки

Опросник «Активность повседневной жизни»

Интересно:

Медицинские крылатые латинские выражения

Роль коммуникаций в менеджменте. Виды коммуникаций

Краткий словарь жестового языка

Что такое кессонный колодец

Обратная связь