При численном решении большого круга задач в конечном итоге происходит их
линеаризация, в связи с чем в соответствующих алгоритмах весьма широко используются
методы линейной алгебры. В их числе:
· решение систем линейных алгебраических уравнений (СЛАУ);
· вычисление определителей матриц;
· нахождение обратных матриц;
· определение собственных значений и собственных векторов матриц.
2 Теоретическая часть.
2.1 Постановка задачи решения СЛАУ:
Многие задачи сводятся к решению систем линейных уравнений. Систему вида
(1)
принято называть системой n линейных алгебраических уравнений (СЛАУ) с n неизвестными. При этом произвольные числа aij (i = 1, 2,…, n; j = 1, 2,…, n) называются коэффициентами системы (коэффициентами при неизвестных), а числа bi (i = 1, 2,…, n) свободными членами. Такая форма записи (1) алгебраической линейной системы называется нормальной. Решением СЛАУ (1) называется совокупность чисел xi (i = 1, 2,…,n), при подстановке которых в систему каждое из ее уравнений обращается в тождество.
Эту систему можно представить в матричном виде: AX = b, где - матрица коэффициентов системы уравнений:
(2)
- вектор неизвестных,
(3)
- вектор правых частей
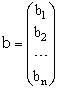(4)
Таким образом
(5)
Перед решением СЛАУ требуется проанализировать корректную постановку задачи.
Система уравнений (5) называется совместной, если она имеет хотя бы одно решение, и несовместной – в противном случае. Совместная система (5) называется определенной, если она имеет единственное решение, и неопределенной, если она имеет больше одного решения.
2.2 Методы решения линейных алгебраических систем.
Принято выделять два класса: прямые (решение за конечное число арифметических операций) и итерационные (обеспечивающие постепенную сходимость к корню уравнения, зависящую от многих факторов).
Прямые методы обычно применяются для решения систем порядка n < 200, для бóльших n используются итерационные методы.
Эффективность способов решения системы (5) во многом определяется свойствами матрицы A (2) (размерностью, симметричностью, заполненностью и т.д.).
3 Практическая часть.
3.1 Задание на курсовую работу:
Решить систему линейных алгебраических уравнений:
· С использование редактора электронных таблиц:
- методом Крамера.
- с помощью обратной матрицы.
· С использованием пакета математического моделирования Matlab
- методом Гаусса.
- методом обратной матрицы.
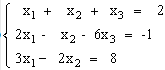
Рис.1. Уравнение 1.
Рис.2. Уравнение 2.
3.2 Решение систем линейных алгебраических уравнений с использование редактора электронных таблиц:
3.2.1 Порядок решения СЛАУ методом Крамера.
Неизвестные x1,x2,…, xn вычисляются по формуле:
где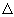 
- определитель матрицы A, 
- определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.
Обратим внимание на особенность работы с матричными формулами: необходимо предварительно выделять область, в которой будет храниться результат, а после получения результата преобразовывать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.
Порядок решения задачи:
· сформировать матрицу коэффициентов и вектор свободных членов заданной системы;
· сформировать четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b;
· вычислить определитель матрицы A, с помощью функции МОПРЕД(d);
· вычислить определитель вспомогательных матриц (d1,d2,d3);
· используя формулы Крамера разделим последовательно определители вспомогательных матриц на определитель матрицы А;
· выполним проверку, умножив вектор Х на исходную матрицу А;
3.2.2 Порядок решения СЛАУ методом обратной матрицы.
- сформировать матрицу коэффициентов и вектор свободных членов заданной системы;
- выделим ячейки для хранения обратной матрицы;
- с помощью функции МОБР найдем обратную матрицу;
- умножим обратную матрицу на столбец вектора b (функция МУМНОЖ), это и будет наш вектор Х;
- выполним проверку, умножив вектор Х на исходную матрицу А;
3.3 Решение заданных уравнений с помощью Excel.
3.3.1 Решение первого уравнения.
Рис.1
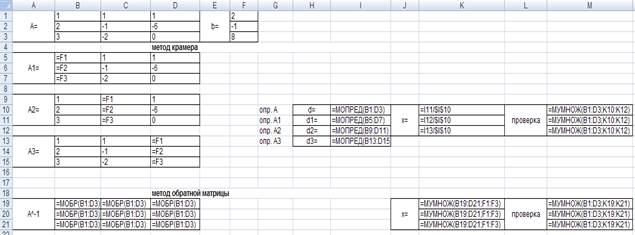
Рис.2
3.3.2 Решение второго уравнения.
Рис.3
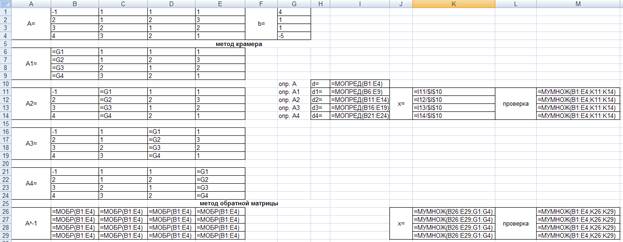
Рис.4
3.4 Описание решения уравнений.
3.4.1 Метод Крамера.
Введём матрицу А и вектор b на рабочий лист. Кроме того, сформируем четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b.
Для дальнейшего решения необходимо вычислить определитель матрицы A. Установим курсор в нужную ячейку и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД, предназначенную для вычисления определителя матрицы, и перейдём ко второму шагу мастера функций. Диалоговое окно, появляющееся на втором шаге, содержит поле ввода Массив. В этом поле указывают диапазон матрицы, определитель которой вычисляют.
В результате получим главный определитель и несколько вспомогательных.
Воспользуемся формулами Крамера и разделим последовательно вспомогательные определители на главный.
В результате вычислений получим вектор Х, который при умножении на исходную матрицу А даст нам вектор b.
3.4.2 Метод обратной матрицы.
Для решения системы методом обратной матрицы необходимо вычислить матрицу, обратную к A. Для этого выделим ячейки для хранения обратной матрицы. Теперь обратимся к мастеру функций, и в категории Математические выберем функцию МОБР, предназначенную для вычисления обратной матрицы, щелкнув по кнопке OK, перейдём ко второму шагу мастера функций. В диалоговом окне, появляющемся на втором шаге мастера функций, необходимо заполнить поле ввода Массив. Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица. Данные в поле ввода Массив можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.
Если поле Массив заполнено, можно нажать кнопку OK. В первой ячейке, выделенного под обратную матрицу диапазона, появится некое число. Для того чтобы получить всю обратную матрицу, необходимо нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter.
Теперь необходимо умножить полученную обратную матрицу на вектор b. Выделим ячейки для хранения результирующего вектора, например. Обратимся к мастеру функций, и в категории Математические выберем функцию МУМНОЖ, которая предназначена для умножения матриц. Напомним, что умножение матриц происходит по правилу строка на столбец и матрицу А можно умножить на матрицу В только в том случае, если количество столбцов матрицы А равно количеству строк матрицы В. Кроме того, при умножении матриц важен порядок сомножителей, т.е. АВ≠ВА.
Перейдём ко второму шагу мастера функций. Появившееся диалоговое окно содержит два поля ввода Массив1 и Массив2. В поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, обратная матрица, а в поле Массив2 ячейки, содержащие вторую матрицу, вектор b.
Если поля ввода заполнены, можно нажать кнопку OK. В первой ячейке выделенного диапазона появится соответствующее число результирующего вектора. Для того чтобы получить весь вектор, необходимо нажать клавишу F2, а затем одновременно клавиши Ctrl+Shift+Enter.
Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор x и получить в результате вектор b. Умножение матрицы A на вектор x осуществляется при помощи функции МУМНОЖ, так как было описанной выше.
3.5 Решение системы линейных алгебраических уравнений с использование пакета математического моделирования Matlab.
3.5.1 Метод Гаусса: Решение системы линейных уравнений при помощи метода Гаусса основывается на том, что от заданной системы, переходят к системе эквивалентной, которая решается проще, чем исходная.
Метод Гаусса состоит из двух этапов:
· Первый этап - это прямой ход, в результате которого расширенная матрица системы путем элементарных преобразований (перестановка уравнений системы, умножение уравнений на число, отличное от нуля, и сложение уравнений) приводится к ступенчатому виду.
· На втором этапе (обратный ход) ступенчатую матрицу преобразуют так, бы в первых n столбцах получилась единичная матрица. Последний, n +1 столбец этой матрицы содержит решение системы линейных уравнений.
Порядок решения задачи в MATLAB следующий:
· Сформировать матрицу коэффициентов 
и вектор свободных членов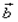 
заданной системы;
· Сформировать расширенную матрицу системы, объединив 
и 
;
· Используя функцию rref, привести расширенную матрицу к ступенчатому виду;
· Найти решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте;
3.5.2 Метод обратной матрицы: для системы из n уравнений с n неизвестными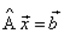 
, при условии что определитель матрицы 
не равен нулю, единственное решение можно представить в виде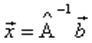 
. Для того чтобы решить систему линейных уравнений методом обратной матрицы, необходимо выполнить следующие действия:
· сформировать матрицу коэффициентов и вектор свободных членов заданной системы;
· решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы, и вектора свободных членов.
3.6 Решение заданных уравнений с помощью MatLab.
3.6.1 Решение первого уравнения.
- Листинг m-файла.
Рис.5
- Выполнение программы.
Рис.6
3.6.2 Решение второго уравнения.
- Листинг m-файла.
Рис.7
- Результат выполнения программы.
Рис.8
3.7 Описание решения уравнений.
Сформируем матрицу А и вектор b из коэффициентов исходного уравнения.
3.7.1 Метод обратной матрицы.
С помощью функции inv найдем обратную матрицу к исходной. Полученную матрицу необходимо умножить для нахождения решения уравнения. Умножив исходную матрицу на тот Х, который мы получили, при правильном решении, это произведение будет равно вектору b.
3.7.2 Метод Гаусса.
С использованием функции rref в переменную С положим сведенную к треугольному виду исходную матрицу. Выделив у получившейся матрицы последний столбец, получим решение исходного уравнения. Если мы умножим матрицу А на решение уравнения и вычтем столбец b, при правильном решении, получи нулевой столбец.
4 Сравнение результатов, полученных при решении. Выводы по работе.
После проведения расчетов указанных систем уравнений, можно сказать, что решения уравнений полученных с помощью пакета математического моделирования MatLab и с помощью электронной таблицы Excel совпадают между собой. Из этого можно сделать вывод о том, что решения систем уравнений не зависит ни от среды решения, ни от способа решения, а отличается лишь функциональным набором и графическим представлением решения.
В данной курсовой работе я более подробно изучила команды и функции в пакете математического моделирования MatLab и Excel,используемых для решения различных математических задач, предназначенных для работы с матрицами.
3.5.2