Получим явное выражение для 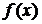 . Поскольку
. Поскольку
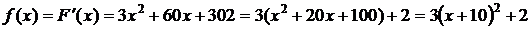 ,
,
имеем:

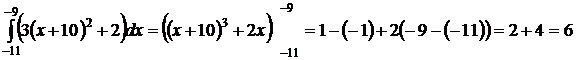
Примечание.
Этот подход можно несколько усовершенствовать. Заметим, что график функции 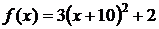 получен сдвигом графика функции
получен сдвигом графика функции 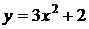 на 10 единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции
на 10 единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции 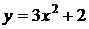 и отрезком
и отрезком 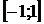 оси абсцисс. Имеем:
оси абсцисс. Имеем:

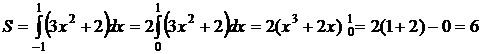
Ответ: 6.
 Задание 8 № 27124
Задание 8 № 27124
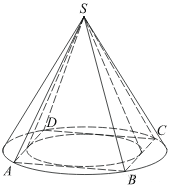
Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Решение
Объемы данных конусов соотносятся как площади их оснований, и, следовательно, как квадраты их диаметров. Диаметр вписанного конуса равен стороне квадрата, диаметр описанного — диагонали квадрата, длина которой равна  длины стороны. Поэтому объем описанного конуса в 2 раза больше объема вписанного.
длины стороны. Поэтому объем описанного конуса в 2 раза больше объема вписанного.
Ответ: 2.
Задание 9 № 26807
Найдите 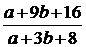 , если
, если 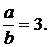
Решение
Из условия 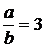 находим, что
находим, что 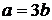 , и подставляем в дробь:
, и подставляем в дробь:
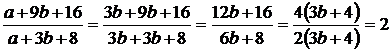
Ответ: 2.
Задание 10 № 27975
В розетку электросети подключены приборы, общее сопротивление которых составляет R 1 = 90 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R 2 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R 1 Ом и R 2 Ом их общее сопротивление даётся формулой 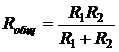 (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в омах.
(Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в омах.
Решение
Задача сводится к решению неравенства 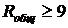 Ом при известном значении сопротивления приборов R 1 = 90 Ом:
Ом при известном значении сопротивления приборов R 1 = 90 Ом:
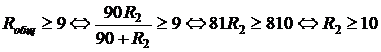 Ом
Ом
Ответ: 10.
Задание 11 № 99595
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
Решение
Пусть v км/ч – скорость второго пешехода, тогда скорость первого – v + 1,5 км/ч. Пусть через t часов расстояние между пешеходами станет равным 0,3 километра. Таким образом,
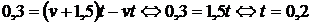 , t = 0,2 часа или 12 минут.
, t = 0,2 часа или 12 минут.
Ответ: 12.
Задание 12 № 26710
Найдите точку минимума функции 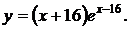
Решение
Найдем производную заданной функции:
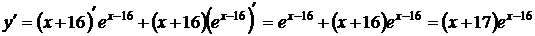 .
.
Найдем нули производной:
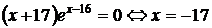 .
.
Определим знаки производной функции и изобразим на рисунке поведение функции:
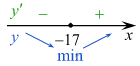
Искомая точка минимума
Ответ: –17.
Задание 13 (С1) № 501215
а) Решите уравнение 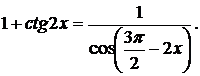
б) Укажите корни этого уравнения, принадлежащие промежутку 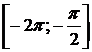 .
.
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в обоих пунктах. | |
| Обоснованно получен верный ответ в пункте а), ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). | |
| Решение не соответствует ни одному из критериев, перечисленных выше. | |
| Максимальный балл |
а) 
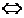
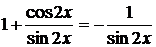
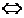
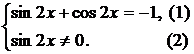
Из уравнения (1) находим:
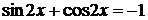
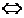
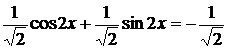
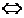
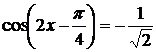
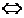
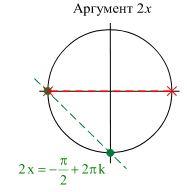
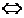
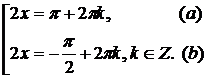
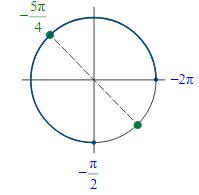 Так как решение (а) не удовлетворяет условию (2), окончательно получаем
Так как решение (а) не удовлетворяет условию (2), окончательно получаем 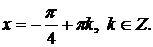
б) Из решений, найденных в пункте а), промежутку 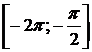 принадлежит только одно число:
принадлежит только одно число: 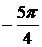 .
.
Ответ: а) 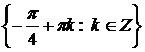 ; б)
; б) 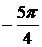 .
.
Задание 14 (С2) № 513920
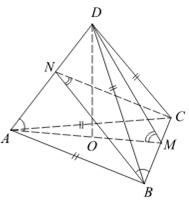
В треугольной пирамиде ABCD двугранные углы при ребрах AD и BC равны. AB = BD = DC = AC = 5.
а) Докажите, что AD = BC.
б) Найдите объем пирамиды, если двугранные углы при AD и BC равны 60°.
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получены верные ответы в пунктах а) и б) | |
| Выполнен только один из пунктов а) или б) | |
| Решение не соответствует ни одному из критериев, приведённых выше | |
| Максимальный балл |
 *Критерии распространяются и на случай использования координатного метода.
*Критерии распространяются и на случай использования координатного метода.
а) Треугольник BAC – равнобедренный. Проведём AM ⊥ BC. M –середина BC, тогда DM ⊥ BC, так как треугольник BDC равнобедренный. ∠ AMD = φ – линейный угол двугранного угла при ребре BC. Аналогично ∠ BNC = φ – линейный угол двугранного угла при ребре AD. Δ ABC = Δ DBC по трём сторонам, тогда MA = MD и 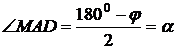
Аналогично Δ BAD = Δ CAD и NB = NC, а
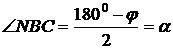 .
.
Треугольники ANM и BMN равны по общему катету MN и острому углу α, тогда AN = BM. Но 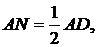
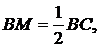 следовательно, AD = BC.
следовательно, AD = BC.
б) По условию φ = 60°, тогда треугольник AMD равносторонний. Пусть AD = AM = MD = BC = a, тогда 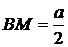 . В треугольнике AMB имеем
. В треугольнике AMB имеем
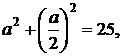 откуда
откуда 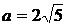 и AD = AM = MD = BC =
и AD = AM = MD = BC = 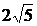 .
.
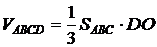 .
.
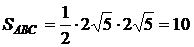 .
.
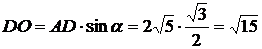 .
.
Тогда
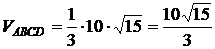 .
.
Ответ: 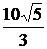 .
.
Задание 15 (С3) № 514625
Решите неравенство 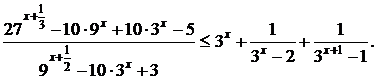
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ | |
| обоснованно получен ответ, отличающийся от верного исключением точки 0, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше. | |
| Максимальный балл |
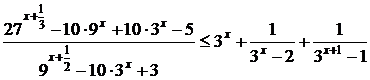
Пусть 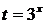 , тогда неравенство примет вид:
, тогда неравенство примет вид:
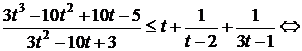
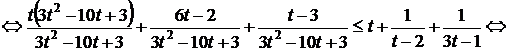
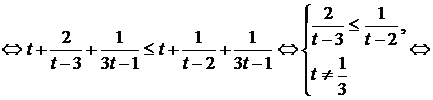
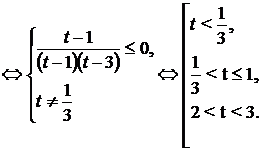
При 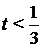 получим:
получим: 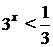 , откуда
, откуда 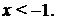
При 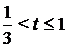 получим:
получим: 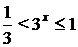 , откуда
, откуда 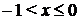 .
.
При 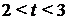 получим:
получим: 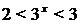 , откуда
, откуда 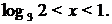
Решение исходного неравенства: 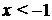 ,
, 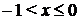 ,
, 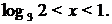
Ответ: 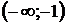 ;
; 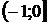 ;
; 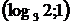 .
.
Задание 16 (С4) № 519661
В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8, AC = 7.
а) Докажите, что вокруг этого четырёхугольника можно описать окружность.
б) Найдите BD.
| Критерии оценивания выполнения задания | Баллы |
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | |
| Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, приведённых выше | |
| Максимальный балл |
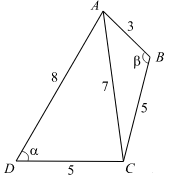
Найдём косинусы углов ABC и ADC в треугольниках ABC и ADC соответственно:
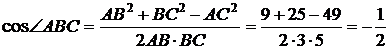 ,
,
поэтому 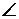 ABC = 120°.
ABC = 120°.
Далее,
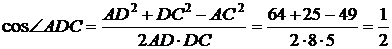 , поэтому
, поэтому 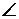 ADC = 60°.
ADC = 60°.
Тем самым, сумма противоположных углов четырехугольника равна 180°, поэтому вокруг него можно описать окружность.
Для вписанного четырёхугольника справедлива теорема Птолемея: произведение диагоналей четырёхугольника равно сумме произведений его противоположных сторон. Тогда АС × BD = AB × DC + AD × BC, то есть 7 BD =
= 3 × 5 + 8 × 5, откуда 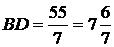 .
.
Ответ: б) 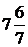 .
.
Приведем решение пункта б) без использования теоремы Птолемея.
Заметим, что 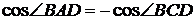 , поскольку
, поскольку 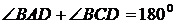 . Пусть
. Пусть  .
.
В треугольнике BAD по теореме косинусов
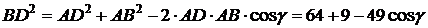 .
.
В треугольнике BCD по теореме косинусов
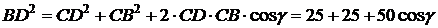
Приравнивая выражения для BD2, получим
 .
.
Тогда 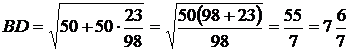 .
.
Ответ: б) 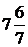 .
.
Задание 17 (С5) № 514450
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен верный ответ | |
| Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат: – неверный ответ из-за вычислительной ошибки; – верный ответ, но решение недостаточно обосновано | |
| Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Пусть повышающий коэффициент 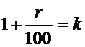 .
.
В соответствии с этим обозначением и условием задачи заполним таблицу:
| Месяц | Долг на 1-е число, млн. руб | Выплата, млн. руб | Долг на 15-е число, млн. руб |
| Январь | |||
| Февраль | k | 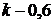
| 0,6 |
| Март | 0,6 k | 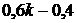
| 0,4 |
| Апрель | 0,4 k | 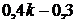
| 0,3 |
| Май | 0,3 k | 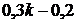
| 0,2 |
| Июнь | 0,2 k | 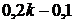
| 0,1 |
| Июль | 0,1 k | 0,1 k |
Найдём общую сумму выплат, сложив ежемесячные выплаты:
(k – 0,6) + (0,6 k – 0,4) + (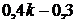 ) + (
) + (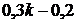 ) + (
) + (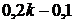 ) + 0,1 k =
) + 0,1 k =
= k (1 + 0,6 + 0,4 + 0,3 + 0,2 + 0,1) – (0,6 + 0,4 + 0,3 + 0,2 + 0,1) = 2,6 k – 1,6
По условию:
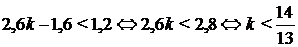
Значит,
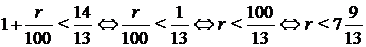 .
.
Откуда наибольшее целое значение
Тем самым, ежемесячно остаток долга возрастал на 7%.
Ответ: r = 7.
Задание 18 (С6) № 505453
Найдите все значения a, при которых уравнение
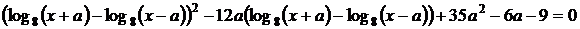 имеет ровно два решения.
имеет ровно два решения.
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен правильный ответ. | |
С помощью верного рассуждения получено множество значений а, отличающееся от искомого только включением точек 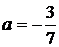 и/или и/или 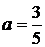 . .
| |
С помощью верного рассуждения получен один из промежутков множества значений а: 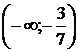 или или 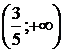 ; возможно, с включением граничных точек и/или исключением точки ; возможно, с включением граничных точек и/или исключением точки 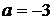 . .
| |
Верно найдена хотя бы одна из граничных точек множества а: 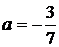 или или 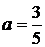 .
ИЛИ
Получено хотя бы одно из уравнений .
ИЛИ
Получено хотя бы одно из уравнений 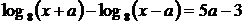 или или 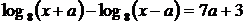 . .
| |
| Решение не соответствует ни одному из критериев, перечисленных выше. | |
| Максимальный балл |
Пусть 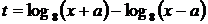 , тогда, используя теорему, обратную теореме Виета, получим:
, тогда, используя теорему, обратную теореме Виета, получим:
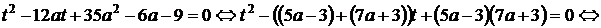
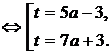
Значит, исходное уравнение имеет два различных корня тогда и только тогда, когда график функции 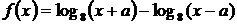 имеет с горизонтальными прямыми
имеет с горизонтальными прямыми 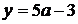 и
и 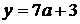 ровно две общие точки. Эти прямые совпадают, если
ровно две общие точки. Эти прямые совпадают, если 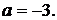
При 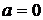 уравнение не имеет решений. Если а > 0, то при х > а, а если а < 0, то при х > – а, имеем:
уравнение не имеет решений. Если а > 0, то при х > а, а если а < 0, то при х > – а, имеем:
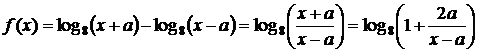 .
.
При неограниченном увеличении х значения функции стремятся к нулю, причём, для а < 0 функция f является возрастающей, а при а > 0 – убывающей. Эскизы графиков изображены на рисунке.
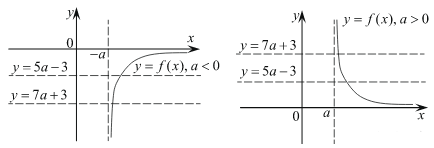
Тем самым, при а > 0, должны быть выполнены неравенства 5 а – 3 > 0, 7 а + 3 > 0, откуда 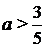 , при а < 0, должны быть выполнены неравенства
, при а < 0, должны быть выполнены неравенства 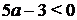 ,
, 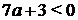 , откуда
, откуда 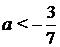 .
.
Ответ: 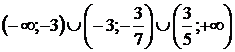 .
.
Приведём авторское решение.
Пусть 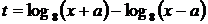 , тогда получим:
, тогда получим:
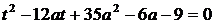
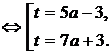
Значит, решение исходного уравнения – это решение уравнений 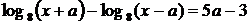 или
или 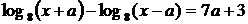 .
.
Исследуем сколько решений имеет уравнение 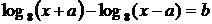 в зависимости от а и b. При
в зависимости от а и b. При 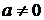 и
и 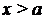 , и
, и 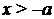 , то есть при
, то есть при 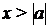 , левая часть определена и принимает вид
, левая часть определена и принимает вид 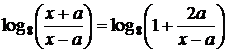 .
.
При 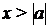 выражение
выражение 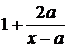 принимает по одному все значенияиз промежутка
принимает по одному все значенияиз промежутка 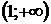 для
для 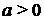 и принимает по одному разу все значения из промежутка (0; 1) для а < 0. Значит, при
и принимает по одному разу все значения из промежутка (0; 1) для а < 0. Значит, при 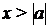 выражение
выражение 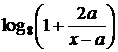 принимает по одному разу все значения промежутка
принимает по одному разу все значения промежутка 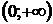 при
при 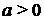 и принимает по одному разу все значения из промежутка
и принимает по одному разу все значения из промежутка 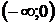 при а < 0. Таким образом, уравнение
при а < 0. Таким образом, уравнение 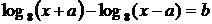 имеет одно решение при
имеет одно решение при 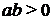 и не имеет решений при
и не имеет решений при 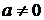 и
и 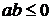 . При
. При 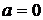 и
и 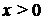 уравнение принимает вид
уравнение принимает вид 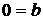 и либо имеет бесконечно много решений, либо не имеет решений.
и либо имеет бесконечно много решений, либо не имеет решений.
Уравнение
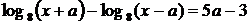 и
и 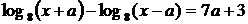 могут иметь общие решения при
могут иметь общие решения при 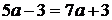 , то есть при
, то есть при 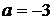 . При
. При 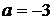 оба уравнения принимают вид
оба уравнения принимают вид 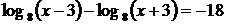 и имеют одно решение.
и имеют одно решение.
При других значениях а исходное уравнение имеет два решения, если оба уравнения 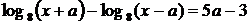 и
и 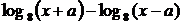 =
=
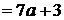 имеют по одному решению. Получаем систему неравенств:
имеют по одному решению. Получаем систему неравенств:
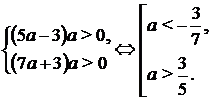
Таким образом, исходное уравнение имеет ровно два решения при а принадлежащем множеству 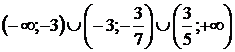 .
.
Задание 19 (С7) № 501734
а) Чему равно число способов записать число 1292 в виде 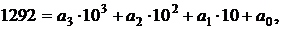 где числа
где числа 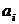 – целые, 0 ≤
– целые, 0 ≤ 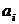 ≤ 99, i = = 0; 1; 2; 3?
≤ 99, i = = 0; 1; 2; 3?
б) Существуют ли 10 различных чисел N таких, что их можно представить в виде 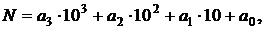 где числа
где числа 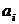 – целые, 0 ≤
– целые, 0 ≤ 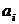 ≤ 99, i = = 0; 1; 2; 3равно 130 способами?
≤ 99, i = = 0; 1; 2; 3равно 130 способами?
в) Сколько существует чисел N таких, что их можно представить в виде 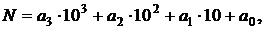 где числа
где числа 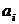 – целые, 0 ≤
– целые, 0 ≤ 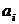 ≤ 99, i = = 0; 1; 2; 3равно 130 способами?
≤ 99, i = = 0; 1; 2; 3равно 130 способами?
| Критерии оценивания выполнения задания | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получен один из следующих результатов: – обоснованное решение п. а; – обоснованное решение п. б; – обоснованная оценка количества задуманных чисел в п. е; – оба набора задуманных чисел в п. в | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Каждое число 0 ≤ 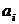 ≤ 99 однозначно представляется в виде
≤ 99 однозначно представляется в виде 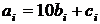 , где 0 ≤
, где 0 ≤ 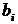 ≤ 9 и 0 ≤
≤ 9 и 0 ≤ 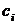 ≤ 9 (i = 0; 1; 2; 3). Значит, для каждого представления некоторого числа N в виде
≤ 9 (i = 0; 1; 2; 3). Значит, для каждого представления некоторого числа N в виде 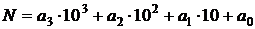 имеет место единственное представление N в виде
имеет место единственное представление N в виде 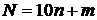 , где
, где 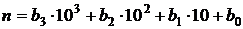 и
и 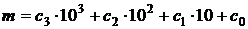 – произвольные целые числа от 0 до 9999. Число способов записать число N в виде
– произвольные целые числа от 0 до 9999. Число способов записать число N в виде 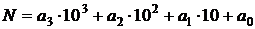 равно числу способов записать число N в виде
равно числу способов записать число N в виде 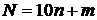 .
.
а) Для представления числа 1292 в виде 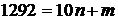 в качестве п можно взять любое целое число от 0 до 129. При этом
в качестве п можно взять любое целое число от 0 до 129. При этом 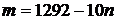 определено однозначно. Таким образом, искомое число способов равно 130.
определено однозначно. Таким образом, искомое число способов равно 130.
б) Повторяя рассуждения предыдущего пункта, несложно показать, что каждое из чисел от 1290 до 1299 представимо в требуемом виде ровно 130 способами.
в) Рассмотрим представление некоторого числа N в виде 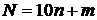 , где п и т – некоторые целые числа от 0 до 9999. Представим т в виде
, где п и т – некоторые целые числа от 0 до 9999. Представим т в виде 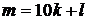 , где l – цифра единиц числа т, а k – некоторое целое число от 0 до 999. Тогда выполнено:
, где l – цифра единиц числа т, а k – некоторое целое число от 0 до 999. Тогда выполнено:
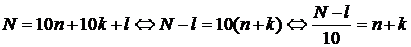 .
.
Найдём все числа К, представимые ровно 130 способами в виде 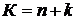 , где п –некоторое целое число от 0 до 9999, а k - некоторое целое число от 0 до 999.
, где п –некоторое целое число от 0 до 9999, а k - некоторое целое число от 0 до 999.
Пусть для некоторого числа К представления 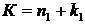 и
и 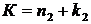 таковы, что п 1 – наименьшее возможное п, а п 2 – наибольшее возможное п. Тогда п 1 = 0 или
таковы, что п 1 – наименьшее возможное п, а п 2 – наибольшее возможное п. Тогда п 1 = 0 или 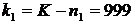 , иначе бы было представление
, иначе бы было представление 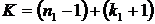 . Аналогично, п 2 = 9999 или
. Аналогично, п 2 = 9999 или 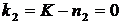 .
.
Заметим, что для любого целого п 0 такого, что 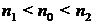 , имеется представление
, имеется представление 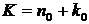 , поскольку
, поскольку 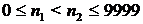 ,
, 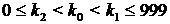 . Таким образом, количество представлений равно п 2 – – п 1 + 1. Если п 1 = 0; п 2 = 9999 или k 1 = 999, k 2 = 0, то представлений больше. Значит, или п 1 = 0; п 2 = 129; K = 129;
. Таким образом, количество представлений равно п 2 – – п 1 + 1. Если п 1 = 0; п 2 = 9999 или k 1 = 999, k 2 = 0, то представлений больше. Значит, или п 1 = 0; п 2 = 129; K = 129; 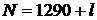 , или п 2 = 9999; п 1 = 9870; k 1 = 999, К = 10869;
, или п 2 = 9999; п 1 = 9870; k 1 = 999, К = 10869; 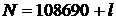 , где l – произвольная цифра. Таким образом, искомое количество чисел равно 20.
, где l – произвольная цифра. Таким образом, искомое количество чисел равно 20.
Ответ: а) 130; б) да; в) 20.