Таблица 1
| № | А | Б | В | Г | А | Б | В | Г | |
 ,
м ,
м
|  ,
м ,
м
| k 03, МН/м3 | k 02, МН/м2 | k 12, МН/м3 | k 30, МН/м3 | k 20, МН/м2 | k 21, МН/м3 | k 11, МН/м2 | |
| -1 | -3 | ||||||||
| -2 | -1 | ||||||||
| -3 | -1 | -1 | |||||||
| -3 | -4 | -4 |
Основные положения теории упругости
 В теории упругости из конструкции сечениями выделяется бесконечно-малый элемент (см.рис.2). На него со всех сторон соседние элементы воздействуют распределенными по поверхности напряжениями σх, σу, σz,…. Они определяются из системы уравнений, которые в общем случае представляют собой совокупность уравнений равновесия, законы Гука, Дюгамеля-Неймана, кинематические соотношения Коши или условия совместности деформаций. Эти уравнения составляются для всех малых элементов и являются объектом изучения теории упругости.
В теории упругости из конструкции сечениями выделяется бесконечно-малый элемент (см.рис.2). На него со всех сторон соседние элементы воздействуют распределенными по поверхности напряжениями σх, σу, σz,…. Они определяются из системы уравнений, которые в общем случае представляют собой совокупность уравнений равновесия, законы Гука, Дюгамеля-Неймана, кинематические соотношения Коши или условия совместности деформаций. Эти уравнения составляются для всех малых элементов и являются объектом изучения теории упругости.
Рассмотрим плоскую задачу теории упругости. Ниже приводятся соотношения для плоского напряженного состояния (ПНС), которое возникает в тонких плитах, балках-стенках, оболочках. Здесь принимают:  (см. рис.3).
(см. рис.3).
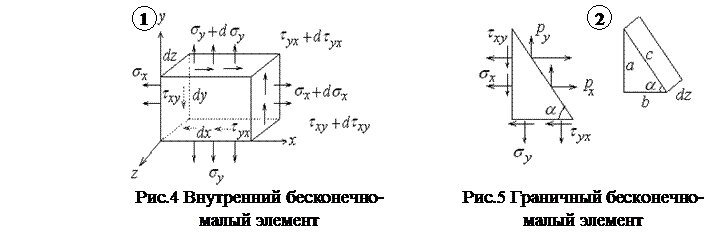
 Дифференциальные уравнения равновесия внутреннего бесконечно-малого элемента 1 (см.рис.2 и рис.4) имеют вид.
Дифференциальные уравнения равновесия внутреннего бесконечно-малого элемента 1 (см.рис.2 и рис.4) имеют вид.
 (1)
(1)
где  - проекции внешней объемной силы на оси координат.
- проекции внешней объемной силы на оси координат.
Алгебраические уравнения равновесия граничного элемента 2 (см.рис.2 и рис.5) имеют вид:


 (2)
(2)
Кинематические соотношения Коши имеют вид:
 (3)
(3)
Закон Гука для ПНС:
 (4)
(4)
где  ,
,  - модуль упругости,
- модуль упругости, 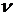 - коэффициент Пуассона
- коэффициент Пуассона
Следствием из соотношений Коши и закона Гука является уравнение совместности деформаций:

 (5)
(5)
где  - Модуль сдвига,
- Модуль сдвига,  - модуль упругости
- модуль упругости
Метод коллокаций
Для решения плоской задачи теории упругости
Суть метода. Искомые напряжения представляются в виде суммы функций с неизвестными коэффициентами. Например:
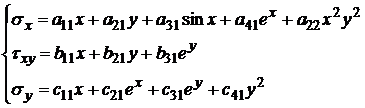 (6)
(6)
Функции при коэффициентах выбираются на усмотрение вычислителя из соображений простоты или точности решения. Обычно удобными являются степенные и тригонометрические функции. Коэффициенты aij, bij, cij – отыскиваются из уравнений равновесия.
Запишем уравнения равновесия (1) для внутреннего элемента i (см.рис.6). Подставляем сюда заданные нами функции для σx, τxy, σy. Тогда получим:
 (7)
(7)


Нашли два уравнения относительно искомых коэффициентов.
Аналогично для i –ого элемента записываются условия совместности деформаций (5):
 (8)
(8)
Кроме внутренних элементов аналогичным образом необходимо записать уравнения равновесия граничных элементов. Например, для граничного элемента j (см. рис.7) уравнения равновесия примут вид:
 (9)
(9)
Обеспечить выполнение этих уравнений во всех элементах обычно не представляется возможным, поэтому удовлетворяем их только в некоторых элементах – элементах коллокации. Поскольку элементы бесконечно малы, то координаты центров этих элементовназываются точками коллокаций. В них мы и удовлетворяем уравнения равновесия.
Число всех точек коллокаций выбирается так, чтобы число уравнений было равно числу всех неизвестных коэффициентов. Из системы алгебраических уравнений (7)-(9) определяются неизвестные aij, bij, cij. Подставляя их в (6), можно получить выражения для напряжения в любой точке.
Пример расчет балки-стенки методом коллокаций
Проведем расчет балки-стенки высотой  и шириной
и шириной  . Поверхностная нагрузка по граням балки-стенки (см. рис.1) меняется по линейному закону. Примем, например,
. Поверхностная нагрузка по граням балки-стенки (см. рис.1) меняется по линейному закону. Примем, например,
 (10)
(10)
Таким образом, для поверхностной нагрузки имеем:
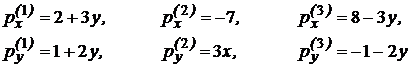 (11)
(11)
 Решение будем искать в виде:
Решение будем искать в виде:
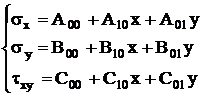 (12)
(12)
В этом случае условие совместности (5) удовлетворяется автоматически (тождественно).
Необходимо определить неизвестные коэффициенты  .
.
Из уравнений равновесия (1) внутреннего элемента 1 (см. рис.8) (первая точка коллокации) получаем:
 (13)
(13)
Составим уравнение равновесия граничного элемента 2 с координатами (0,y):
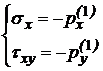
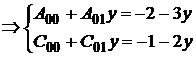 (14)
(14)
Аналогично для граничного элемента 3 с координатами (x,h):
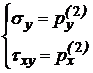
 (15)
(15)
Для граничного элемента 4 с координатами (b,y):

 (16)
(16)
Таким образом, неизвестны 9 коэффициентов  согласно выражениям (12). Необходимо составить 9 алгебраических уравнений. Для этого берем следующие конкретные точки коллокации граничных элементов.
согласно выражениям (12). Необходимо составить 9 алгебраических уравнений. Для этого берем следующие конкретные точки коллокации граничных элементов.
Согласно (14) для второй точки коллокации с координатами (0,0):
 (17)
(17)
По уравнениям (15) для третьей точки коллокаций с координатами (0,h):
 (18)
(18)
Согласно (15) для четвертой точки коллокаций с координатами (b,h):
 (19)
(19)
По выражениям (16) для пятой точки коллокаций с координатами (b,h/2):
 (20)
(20)
Таким образом, из 10 уравнений одно можно убрать (на усмотрение расчетчика), поскольку решение получается приближенное.
Разрешив систему уравнений (13), (17)-(20), получаем следующие искомые константы:
 (21)
(21)
Окончательно выражения для напряжений примут вид:
 (22)
(22)
На рис.9, рис.10, рис.11 построены эпюры напряжений  в сечениях
в сечениях 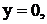
 ,
, 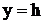 .
.
Расчет на прочность
Для бетона в случае ПНС применим критерий Г.А. Гениева, который имеет вид:
 (23)
(23)
Здесь  -расчетные значения сопротивлению бетона сжатию и растяжению соответственно,
-расчетные значения сопротивлению бетона сжатию и растяжению соответственно,  - -главные напряжения.
- -главные напряжения.
Например, примем в расчетах марку бетона B30, для которого  .
.
Главные напряжения  , как известно, определяются по формулам:
, как известно, определяются по формулам:
 (24)
(24)
Определим по эпюрам напряжений (рис.9 - рис.11) опасные точки в поперечном сечении. На рис. 12 изображены опасные точки. Проверим прочность в каждой из них.
 Прочность в точке А
Прочность в точке А


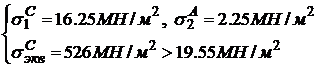

ВЫВОД
Прочность нарушается в каждой из опасных точек. Таким образом, заданное нагружение балки-стенки неприемлемо.

Ниже в приложении 1 приведен пример численного расчета рассмотренной задачи с применением прикладного пакета MATHEMATICA 5.
Приложение 1
Пример численного расчета данного задания
с применением прикладного пакета MATHEMATICA 5.
<<Graphics`FilledPlot`
"ВЫСОТА И ШИРИНА ПОПЕРЕЧНОГО СЕЧЕНИЯ БАЛКИ-СТЕНКИ";
h=3;
b=5;
"ВХОДНЫЕ ПАРАМЕТРЫДЛЯ ПОВЕРХНОСТНОЙ НАГРУЗКИ";
k11:=1;
k12=1;
k21=0;
k02=-1;
k20=0;
k30=1;
k03=-1;
"ВЫРАЖЕНИЯ ДЛЯ ПОВЕРХНОСТНОЙ НАГРУЗКИ НА ЛЕВОЙ,ПРАВОЙ И ВЕРХНЕЙ ГРАНИ ПОПЕРЕЧНОГО СЕЧЕНИЯ БАЛКИ-СТЕНКИ";
Px1[y_]:=-3*k03*y-2*k02;
Py1[y_]:=2*k12*y+k11;
Px3[y_]:=3*k03*y+2*k02+2*k12*b;
Py3[y_]:=-2*k12*y-2*k21*b-k11;
Px2[x_]:=-2*k21*x-2*k12*h-k11;
Py2[x_]:=3*k30*x+2*k20+2*k21*h;
"АППРОКСИМАЦИЯ НАПРЯЖЕНИЙ ЛИНЕЙНЫМИ ФУНКЦИЯМИ С НЕИЗВЕСТНЫМИ КОЭФФИЦИЕНТАМИ";


A10+C01Š0
B01+C10Š0
" РЕШЕНИЕ СИСТЕМЫЛИНЕЙНЫХ УРАВНЕНИЙ ДЛЯ ОПРЕДЕЛЕНИЯ НЕИЗВЕСТНЫХ КОЭФФИЦИЕНТОВ В ВЫРАЖЕНИЯХ ДЛЯ НАПРЯЖЕНИЙ";
"СИСТЕМА СОСТАВЛЕНА ИЗ УРАВНЕНИЙ РАВНОВЕСИЯ ДЛЯ ВНУТРЕННЕГО ЭЛЕМЕНТА И ИЗ УРАВНЕНИЙ РАВНОВЕСИЯ В ТОЧКАХ КОЛЛОКАЦИЙ ГРАНИЧНЫХ ЭЛЕМЕНТОВ ";

{{A00®-2,A10®2,A01®-3,B00®0,B10®3,B01®0,C00®-1,C10®0,C01®-2}}

-2+2 x-3 y
3 x
-1-2 y


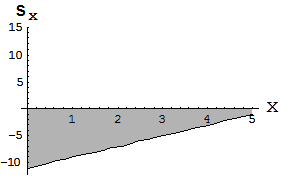
…Graphics…


…Graphics…


…Graphics…



…Graphics…


…Graphics…


…Graphics…



…Graphics…


…Graphics…

…Graphics…