Метод Власова. Из вариационных методов приведения дифференциальных уравнений в частных производных к обыкновенным дифференциальным уравнениям остановимся на методе В. З. Власова.
В исследуемой пластинке будем различать два направления; поперечное, совпадающее с направлением оси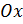 
, и продольное, совпадающее с направлением 
.
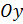На продольных краях пластинки могут быть заданы граничные условия как геометрические, так и статические, всего по два условия на каждом крае. Для всякой линии 
прогиб пластинки 
представляет собой непрерывную упругую линию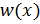 
, удовлетворяющую на концах (на продольных краях пластинки) заданным геометрическим граничным условиям. Пусть эта упругая линия 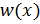может быть представлена при помощи 
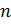линейно независимых функций 
, удовлетворяющих тем же геометрическим условиям, что и 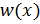, т.е.
(а)
Функции являются безразмерными, а коэффициенты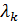 
имеют размерность прогиба 
.
Переходя от линии 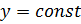к другой, смежной с ней, замечаем, что вследствие непрерывности функции 
значения числовых коэффициентов 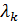будут меняться как непрерывные функции от 
. Следовательно, функция прогибов может быть представлена в виде разложения
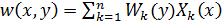(б)
Одну из двух систем функци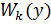й 
или 
можно выбрать заранее и в дальнейшем считать заданной. Будем считать заданной систему безразмерных функций : тогда функции 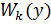, имеющие размерность прогиба, будут искомыми коэффициентами разложения.
В соответствии с размерностями и физическим смыслом формулы (б) функции 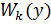называются обобщенными прогибами, а функции - функциями поперечного распределения прогибов.
Представление изогнутой срединной поверхности пластинки в виде разложения (б) при конечном числе 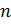означает, что пластинка заменена системой с конечным числом степеней свободы в поперечном направлении при сохранении бесконечного числа степеней свободы в продольном направлении. Это означает также приведение двухмерной задачи изгиба пластинки к одномерной, ибо после того, как найдены все 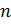функций 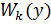, значение прогибов будут определены с известной степенью точности.
Выбор функции прогибов в виде конечного ряда (б) предполагает приближенное решение задачи. В общем случае функция (б) не будет удовлетворять уравнению Софи Жермен. Поэтому для определения функций 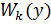воспользуемся вариационным методом Бубнова-Галернкина. Вариационное уравнение Бубнова- Галеркина (8.1) для решаемой задачи при обычном расположении осей можно представить в такой форме:
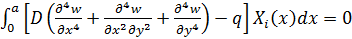. (в)
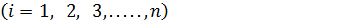
Согласно зависимостям между усилиями и прогибами теории изгиба пластинок, разность значений изгибающих моментов Mx и приведенных поперечных сил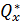 
, вычисленных для краевых сечений х=0 и х=а, составит: 
(г)
.
Применяя интегрирование по частям уравнения (в), с учетом соотношений (г), получим интегро-дифференциальное уравнение, в которое войдут в качестве свободных членов
и 
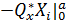, (д)
представляющие собой отнесенную к единице длины работу разности краевых изгибающих моментов Mx и приведенных поперечных сил 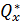,приложенных в сечениях х=0 и х=а пластинки. Причисляя эту работу к суммарной работе внешней нагрузке q и подставляя функцию (б), получим вариационное уравнение равновесия в окончательном виде:
- 2 
+ 
- 
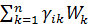=0. (e)
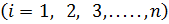
Здесь коэффициенты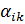 
, 
, 
определяются только выбранной системой функций поперечного распределения прогибов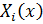 
и обладают свойством взаимности, а свободные члены зависят от нагрузки q, цилиндрической жесткости D и разности краевых усилий (г).
Метод Курдюмова-Кочанова. При использовании метода Бубнова-Галёркина линейно независимые функции в выражении для перемещений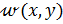 
должны быть выбраны так, чтобы все краевые условия рассматриваемой задачи тождественно выполнялись. При достаточно сложных граничных условиях выполнение этого требования становится весьма затруднительным. Этого недостатка лишен метод Курдюмова-Кочанова, который, как и метод Бубнова-Галёркина, применяем для получения приближенного решения как линейных, так и нелинейных одномерных и многомерных краевых задач.
Изложим сущность этого метода на примере решения одномерной задачи, описываемой дифференциальным уравнением
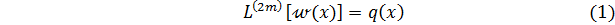
при краевых условиях
где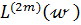 
, 
и 
‒заданные дифференциальные операторы;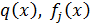 
и 
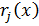‒ заданные функции.
Решение уравнения (1) ищем в виде
где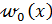 
‒ общий интеграл некоторого упрощенного дифференциального уравнения (линейного с постоянными коэффициентами) того же порядка, что и исходное уравнение,
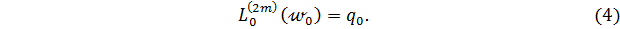
В частности, в качестве 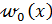можно взять общий интеграл простейшего дифференциального уравнения 
-го порядка:
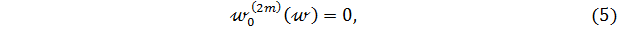
отсюда получим
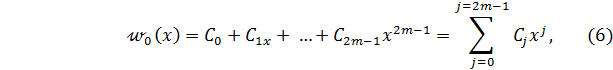
где 
‒ произвольные постоянные интегрирования.
С учетом зависимости (3) непосредственно из уравнения (1) можно получить дифференциальное уравнение для определения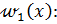 
Частное решение уравнения (7) будем искать в виде
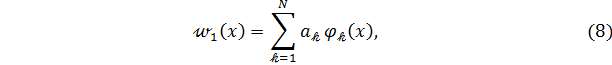
где 
неизвестные параметры, а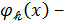 
система функций, удовлетворяю-щая лишь условиям полноты.
Целесообразно выбрать такую систему функций 
, которая приводила бы к максимальному упрощению процедуры определения частного решения уравнения (7). Этому требованию в наибольшей степени удовлетворяет система функций
Тогда
Для определения неизвестных 
воспользуемся методом Бубнова-Галёркина:
После подстановки (6) и (9) в (10) и выполнения преобразований, получим систему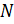 
алгебраических уравнений относительно неизвестных параметров (
) и постоянных интегрирования (
).
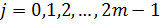Полученную систему 𝑁 уравнений необходимо дополнить системой алгебраических уравнений, которые найдем из граничных условий (2) после подстановки в них функции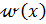 
, определяемой суммо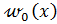й 
и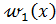 
.
Решая совместно эти две системы алгебраических уравнений, сможем определить неизвестные параметры 
и постоянные интегрирования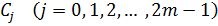 
, после чего по формулам (6) и (9) определяются функци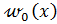и и 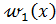, а по формуле (3) ‒ решение рассматриваемой краевой задачи .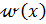