Томский государственный университет систем управления и радиоэлектроники
Приходовский М.А.
Математика - 1 семестр
Курс лекций
Учебное пособие
Для специальностей
Информатика и вычислительная техника»
Инфокоммуникационные технологии и системы связи»
Радиоэлектронные системы и комплексы»
Томск
ТУСУР
Элементы векторной алгебры.
Скалярное, векторное, смешанное произведение.
Скалярное произведение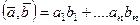 
хорошо известно из школьного курса.
Если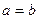 
то получаем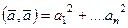 
.
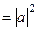Скалярное произведение обладает хорошо известным свойством:
.
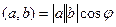Чтобы его запомнить, рассмотрим идею доказательства. Расположим первый вектор на оси Ох, пусть его координаты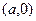 
, второй вектор 
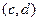. Тогда их скалярное произведение равно 
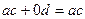. С другой стороны, произведение модулей на косинус угла:
.
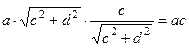Векторное произведение.
Определение. Вектор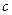 
называется векторным произведением векторов 
, обозначается 
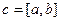, если выполнены 3 условия:
1) 
, 
.
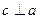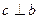2) Векторы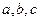 
образуют правоориентированную тройку, то есть с конца вектора 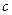кратчайший поворот от 
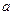к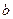 
виден против часовой стрелки.
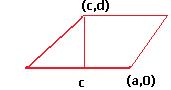
3) 
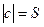параллелограмма, образованного парой векторов 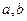, то есть 
.
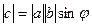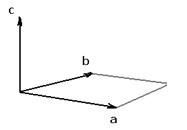
Таблица свойств скалярного и векторного произведений:
сходство и различия.
| 
|
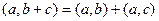
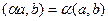
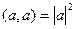
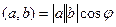
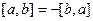
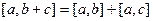
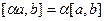
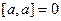
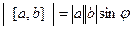
Метод нахождения векторного произведения с помощью определителя: Можно записать в 1-ю и 2-ю строку исходные два вектора, в третьей строке добавить произвольные обозначения осей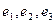 
, и вычислить этот определитель.
= 
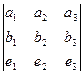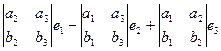. Миноры порядка 2 вычислятся, эти числа как раз и будут координатами 
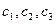нового вектора, который является векторным произведением.
Пример. Найти векторное произведение векторов (1,1,1) и (1,2,3)
= 
= 
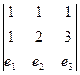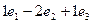. Ответ (1,-2,1).
Также можно проверить, что он действительно перпендикулярен исходным векторам (скалярно умножить на 1-й или на 2-й вектор, получим 0).
Примечание. Определитель можно вычислять либо разложением по 3-й строке, либо ранее известными методами, в том числе добавить копии двух первых столбцов справа.
Смешанное произведение. Определеятся так: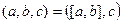 
.
Этот объект корректно определён и существует: векторное произведение первой пары есть какой-то вектор, и его можно скалярно умножить на ещё один, третий вектор, в итоге получится константа.
Смешанное произведение вычисляется с помощью определителя так: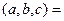 
.
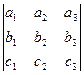Обоснование: Если рассмотреть разложение этого определителя по третьей строке, то получится
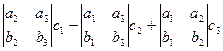, то есть 1-я координата векторного произведения 
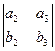как раз и умножается на 1-ю координату вектора 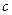, 2-я на 2-ю и т.д. то есть это и есть 
.
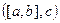Геометрический смысл: объём параллелепипеда, образованного тремя векторами.
Практика
Элементы векторной алгебры.
Задача 58. Найти скалярное и векторное произведение векторов (1,1,1) и (1,2,3).
Решение. Скалярное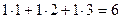 
.
Векторное = = .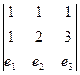
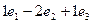Ответ. Скалярное 6, векторное (1,-2,1).
Замечание. Можно проверить, что (1,-2,1) перпендикулярен исходным векторам (скалярно умножить на 1-й или на 2-й вектор, получим 0).
Задача 59. Найти скалярное и векторное произведение векторов:
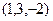и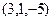 
.
Решение.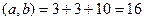 
.
Для поиска векторого произведения запишем определитель.
= 
= 
.
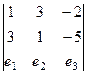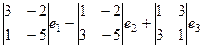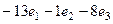Ответ. Скалярное: 16, векторное: (-13, -1, -8).
Задача 60. Дано: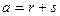 
, 
, 
, 
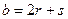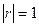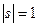, угол между векторами 
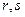45 градусов. Найти 
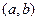и 
.
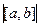Решение.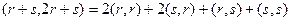 
= 
= 
.
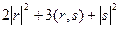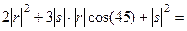
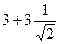Примечание. Как видим, можно вычислять скалярное произведение, даже не зная координат векторов. Здесь фактически 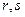служат в качестве базисных векторов, и через них выражены 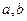, то есть (1,1) и (2,1) координаты 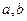относительно базиса 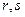. Вся эта система целиком может двигаться или вращаться, но углы между векторами и их длины при этом не поменяются. Поэтому конкретных координат и нет, и они для решения задачи и не нужны.
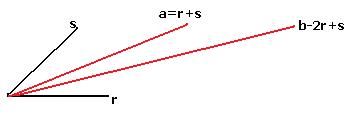
Пункт Б. =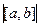 
= 
=
= 
= 
.
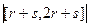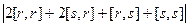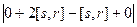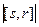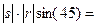
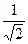Ответ. 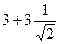и .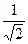
Задачи 61,62,63. Векторы a,b выражены через p,r: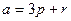 
, 
. 
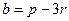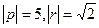, угол между ними 45 град.
Задача 61. Найти .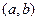
Задача 62. Найти | [a,b] |.
Задача 63. Найти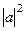 
.
Решение задачи 61.
= 
= 
.
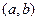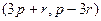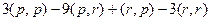Мы раскрыли скобки, используя свойства скалярного произведения. Далее, так как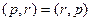 
то объединим их, и получим 
.
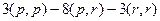Это можно выразить так:
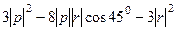и получаем 
.
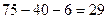Ответ. 29.
Решение задачи 62.
= 
= 
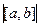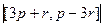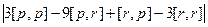
Несмотря на то, что скобки мы раскрыли похожим образом, дальше будет существенное отличие, т.к. свойства векторного произведения совсем другие, чем скалярного. Так,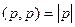 
, но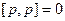 
. Кроме того, чтобы объединить 
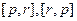в одно слагаемое, здесь надо сначала у одной из них сменить знак.
= 
=
= 
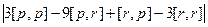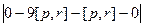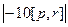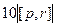. Модуль векторного произведения 
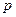и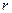 
это площадь параллелограмма, где эти векторы являются сторонами, поэтому далее можно продолжить так:
= 
= 
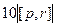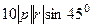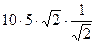= 50. Ответ. 50.
Решение задачи 63.
= 
= 
= 
=
= 
=
= 
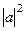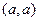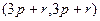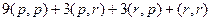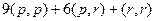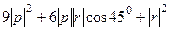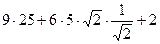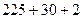= 257. Ответ. 257.
Задача 64. Найти смешанное произведение трёх векторов:
.
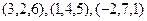Решение. Вычислим определитель:
= 
= 
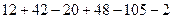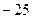. Ответ. .
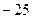Задача 65. Найти косинус угла между векторами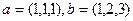 
.
Решение.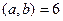 
, 
, 
,
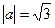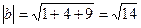учитывая ч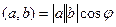то , то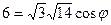 
.
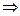
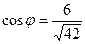Заметим, что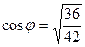 
, т.е. чуть меньше 1, угол близок к 0.
Ответ. .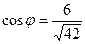
Задача 66. Найти косинус угла между векторами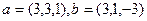 
.
Решение.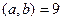 
, 
, 
,
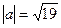учитывая ч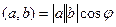то , то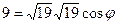 
.
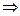
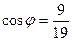Оценим приблизительно, какой это угол. Заметим, что если было бы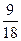 
то было бы 
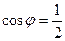и угол 600.
В данном случае косинус чуть меньше, а значит угол чуть больше 600.
Ответ. .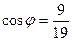
Задача 67. Вычислить площадь параллелограмма, образованного векторами 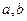, если 
, 
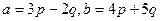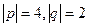, угол между p,q равен 
.
Решение.
Площадь параллелограмма - значит, надо вычислить модуль векторного произведения =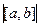 
= 
=
= 
= 
= 
=
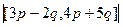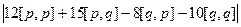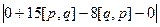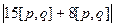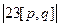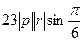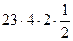= 92.
Ответ 92.
Задача 68 и 69. Векторы a,b выражены через p,q: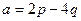 
, 
. 
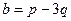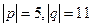, угол между ними 600.
Задача 68. Найти .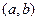
Решение. =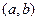 
= 
= 
= 
=
= 
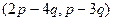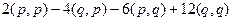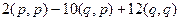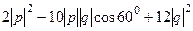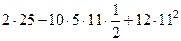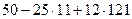= 1227.
Ответ. 1227.
Задача 69. Найти | [a,b] |.
Решение.
| [a,b] | = |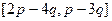 
|= | 
| = | 
| = | 
| = 
=
= 
.
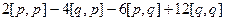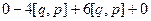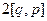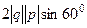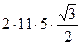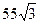Ответ. .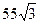
Задача 70. Вывести формулу проекции вектора на ось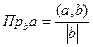 
.
Решение. 1) известно, что .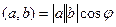
2) длина проекции 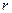это катет, 
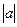гипотенуза треугольника, тогда получается, что 
.
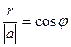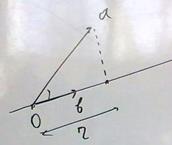
Сопоставим эти 2 факта.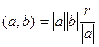 
, тогда 
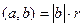, откуда и следует 
.
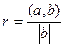Задача 71. Найти проекцию вектора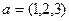 
на линию, порождаемую вектором 
.
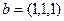Решение. По формуле =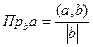 
= 
= 
.
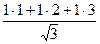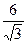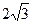Ответ. 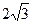.