Перейдем теперь к рассмотрению равновесных свойств электронной подсистемы в полупроводниках и металлах. Как отмечалось, приближение самосогласованного поля позволяет задачу об электронной подсистеме свести к задаче об идеальном электронном газе.
Начнем мы с рассмотрения электронов проводимости.Как мы знаем, в отсутствие внешних полей одноэлектронный базис мы можем сформировать из блоховских состояний. Эти состояния задаются двумя квантовыми числами - квазиволновым вектором  , определяющим координатную часть волновой функции, и спиновым квантовым числом
, определяющим координатную часть волновой функции, и спиновым квантовым числом  , определяющим спиновую компоненту волновой функции. Поскольку в состоянии термодинамиеского равновесия с подавляющей вероятностью реализуются микросостояния, в которых подавляющая часть электронов находится вблизи дна зоны проводимости, то в наших расчетах мы можем рассматривать только такие одноэлектронные состояния. Для простоты будем рассматривать случай невырожденной зоны с изотропным параболическим законом дисперсии.
, определяющим спиновую компоненту волновой функции. Поскольку в состоянии термодинамиеского равновесия с подавляющей вероятностью реализуются микросостояния, в которых подавляющая часть электронов находится вблизи дна зоны проводимости, то в наших расчетах мы можем рассматривать только такие одноэлектронные состояния. Для простоты будем рассматривать случай невырожденной зоны с изотропным параболическим законом дисперсии.
 , (1)
, (1)
где 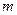 - эффективная масса у дна зоны проводимости. Энергию мы отсчитываем от дна зоны.
- эффективная масса у дна зоны проводимости. Энергию мы отсчитываем от дна зоны.
Найдем плотность одночастичных стационарных состояний. По определению она есть
 . (2)
. (2)
В рассматриваемом случае энергия  одночастичного стационарного состояния вырождена по спиновому квантовому числу. Поэтому выражение под знаком суммы не зависит от спинового квантового числа
одночастичного стационарного состояния вырождена по спиновому квантовому числу. Поэтому выражение под знаком суммы не зависит от спинового квантового числа  , и вся сумма разбивается на две независимые суммы - по
, и вся сумма разбивается на две независимые суммы - по  и
и 
 . (3)
. (3)
У электрона спиновое квантовое число может принимать только два значения  . Поэтому
. Поэтому
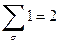 , (4)
, (4)
и таким образом,
 . (5)
. (5)
Пользуя квазинепрерывный характер спектра квазиволнового вектора, заменяем сумму на интеграл
 . (6)
. (6)
Подынтегральное выражение не зависит от направления волнового вектора  . Поэтому интеграл разумно вычислять в сферической системе координат. Тогда интегрирование по углам дает полный телесный угол, и мы получаем
. Поэтому интеграл разумно вычислять в сферической системе координат. Тогда интегрирование по углам дает полный телесный угол, и мы получаем
 . (7)
. (7)
Перейдя к новой переменной  интегрирования, находим
интегрирования, находим
 . (8)
. (8)
Воспользовавшись основным свойством дельта-функции Дирака, получаем
 , (9)
, (9)
где
 . (10)
. (10)
- тета-функция Хэвисайда.
Таким образом, для среднего числа частиц и внутренней энергии имеем
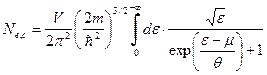 (11)
(11)
и
 . (12)
. (12)
Рассмотрим вначале электроны проводимости металла. В металле в качестве свободных носителей заряда выступают только электроны в зоне проводимости. Остальные электроны прочно связаны со своими ядрами и при обычных условиях не возбуждаются. Поэтому число электронов в зоне проводимости мы можем рассматривать как заданную постоянную величину, и определять химический потенциал из уравнения (11).
Начнем изучение термодинамических свойств нашего электронного газ с рассмотрения простейшего случая  .
.
Прежде всего, установим, как в этом случае выглядит распределение Ферми-Дирака.
В случае, когда газ находится при температуре  , среднее число частиц в одночастичном стационарном состоянии с волновым вектором
, среднее число частиц в одночастичном стационарном состоянии с волновым вектором  и спиновым числом
и спиновым числом  - оно же вероятность заполнения этого одночастичного стационарного состояния - имеет вид
- оно же вероятность заполнения этого одночастичного стационарного состояния - имеет вид
 . (13)
. (13)
Для того, чтобы получить распределение Ферми-Дирака при абсолютном нуле температуры, мы должны в выражении (13) перейти к пределу  .
.
Прежде всего, определим знак химического потенциала. В принципе, возможны три варианта – химический потенциал является отрицательным, равным нулю или положительным. Давайте посмотрим, что будет происходить в каждом из этих случаев.
Пусть химический потенциал является отрицательным. Поскольку все уровни энергии  , то для любого
, то для любого  числитель аргумента экспоненты
числитель аргумента экспоненты  , и, соответственно,
, и, соответственно,  . Но тогда мы получаем, что при абсолютном нуле температуры вероятность заполнения всех одночастичных состояний равна нулю. Это явное противоречие. Таким образом, мы приходим к выводу, что химический потенциал нашего электронного газа в принципе не может быть отрицательным.
. Но тогда мы получаем, что при абсолютном нуле температуры вероятность заполнения всех одночастичных состояний равна нулю. Это явное противоречие. Таким образом, мы приходим к выводу, что химический потенциал нашего электронного газа в принципе не может быть отрицательным.
Пусть теперь химический потенциал  . Тогда при
. Тогда при  отлична от нуля вероятность заполнения только двух состояний с
отлична от нуля вероятность заполнения только двух состояний с  =0. Однако принцип Паули позволяет в этих двух состояниях находиться только двум электронам, и мы вновь получаем явное противоречие.
=0. Однако принцип Паули позволяет в этих двух состояниях находиться только двум электронам, и мы вновь получаем явное противоречие.
Таким образом, мы приходим к выводу, что химический электронного газа в металле может быть только положительным.
Тогда устремив в выражении (78)  , получаем следующее выражение для распределения Ферми-Дирака при абсолютном нуле температуры
, получаем следующее выражение для распределения Ферми-Дирака при абсолютном нуле температуры
 . (14)
. (14)
Здесь обозначено
 . (15)
. (15)
Если теперь вспомнить, что согласно принципу запрета Паули в каждом одночастичном состоянии не может находиться более одного электрона, то легко видеть, что при абсолютном нуле температуры реализуются только микросостояния газа с наименьшей возможной энергией. То есть отлична от нуля только вероятность основного микросостояния. Вероятность же всех возбужденных состояний равна нулю. В основном микросостоянии электроны заполняют в соответствии с принципом Паули N низших по энергии одночпастичных стационарных состояний. Наибольшая энергия занятого одночастичного состояния в основном микросостоянии ферми-газа называется энергией Ферми. Таким образом, при абсолютном нуле температуры химический потенциал электронного газа в металле совпадает с его энергией Ферми.
Подставляя (14) в уравнение (11), получаем
 . (16)
. (16)
Отсюда энергия Ферми
 , (17)
, (17)
где
 (18)
(18)
- волновой вектор Ферми,  - концентрация газа.
- концентрация газа.
Внутренняя энергия при Т=0

 . (19)
. (19)

В соответствии с общим термодинамическим соотношением свободная энергия
 . (20)
. (20)
соответственно, при абсолютном нуле
 . (21)
. (21)
Тогда давление при Т=0

 (22)
(22)

При конечной температуре становится отличной от нуля также и вероятность возбужденных микросостояний. Как легко видеть непосредственно из распределения Ферми-Дирака (78), при конечной температуре вероятность заполнения одночастичного состояния с энергией, превышающей энергию Ферми, заметно отлична от нуля только тогда, когда энергия этого состояния отстоит от энергии Ферми на величину, меньшую, либо порядка  :
:  ~
~  . Поэтому с подавляющей вероятностью реализуются микросостояния газа, в которых подавляющая часть электронов заселяет одночастичные состояния с энергией
. Поэтому с подавляющей вероятностью реализуются микросостояния газа, в которых подавляющая часть электронов заселяет одночастичные состояния с энергией  ~
~  . В этих микросостояниях доля электронов, заселяющих одночастичные состояния с энергией, большей
. В этих микросостояниях доля электронов, заселяющих одночастичные состояния с энергией, большей  , определяется отношением
, определяется отношением  .
.
Поэтому для достаточно низких температур, когда 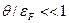 с подавляющей вероятностью реализуются микросостояния, в которых подавляющая часть электронов заселяет одночастичные состояния с энергией, не превышающей энергию Ферми. Такой электронный газ называется вырожденным.
с подавляющей вероятностью реализуются микросостояния, в которых подавляющая часть электронов заселяет одночастичные состояния с энергией, не превышающей энергию Ферми. Такой электронный газ называется вырожденным.
Параметр, определяющий степень вырождения, есть  . Чем меньше это отношение, тем сильнее вырожден газ. Максимальное вырождение газа имеет место при абсолютном нуле температуры.
. Чем меньше это отношение, тем сильнее вырожден газ. Максимальное вырождение газа имеет место при абсолютном нуле температуры.
Соответственно, условие вырождения газа есть
 . (23)
. (23)
Используя выражение (82) для энергии Ферми, условие вырождения можно записать как
 . (24)
. (24)
Отсюда видно, что чем больше концентрация, тем в большей области температур электронный газ можно считать вырожденным. Поскольку в металлах концентрация электронов достаточно велика, то газ электронов проводимости в металлах является сильно вырожденным даже при комнатных температурах, а во многих случаях и вплоть до температуры плавления.
Таким образом, при вычислении электронной теплоемкости металла мы можем считать электронный газ вырожденным. Найдем химический потенциал и теплоемкость вырожденного электронного газа.
Введем обозначение
 , (25)
, (25)
Тогда уравнение для химического потенциала и выражение для внутренней энергии можно записать в виде
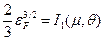 (26)
(26)
и
 , (27)
, (27)
Таким образом, наша задача свелась к вычислению интеграла
 , (28)
, (28)
где n-целое положительное число. Поскольку мы рассматриваем вырожденный газ, то при вычислении этого интеграла нужно воспользоваться тем, что  .
.
Выполнив обезразмеривающую замену переменной  , получаем
, получаем
 . (29)
. (29)
Точкой  разбиваем область интегрирования на две части
разбиваем область интегрирования на две части 
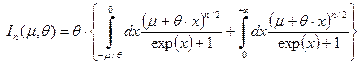 . (30)
. (30)
В первом интеграле делаем замену  , и после несложных преобразований находим
, и после несложных преобразований находим
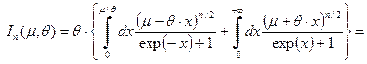 .
.

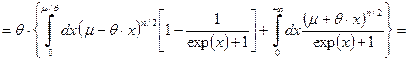
 (31)
(31)

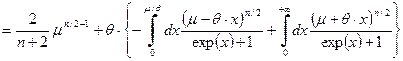 .
.
Мы рассматриваем вырожденный электронный газ. Поэтому у нас  . В знаменателе подынтегрального выражения присутствует экспонента. Поэтому подынтегральная функция быстро стремится к нулю с ростом х. Основной вклад в этот интеграл дают x<~1. Следовательно, второй интеграл как функция верхнего предела
. В знаменателе подынтегрального выражения присутствует экспонента. Поэтому подынтегральная функция быстро стремится к нулю с ростом х. Основной вклад в этот интеграл дают x<~1. Следовательно, второй интеграл как функция верхнего предела  быстро сходится к своему значению с бесконечно большим верхним пределом. При
быстро сходится к своему значению с бесконечно большим верхним пределом. При  этот интеграл практически не будет отличаться от своего значения с бесконечно большим пределом. Поэтому в случае вырожденного электронного газа верхний предел второго интеграла можно с большой точностью заменить на
этот интеграл практически не будет отличаться от своего значения с бесконечно большим пределом. Поэтому в случае вырожденного электронного газа верхний предел второго интеграла можно с большой точностью заменить на  .
.
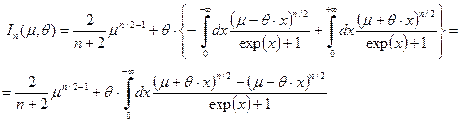 . (32)
. (32)
 .Поскольку основной вклад в интеграл дают x<~1 и
.Поскольку основной вклад в интеграл дают x<~1 и  , то функции
, то функции  под знаком интеграла можно разложить в ряд Тейлора в окрестности нуля. Ошибка будет очень мала. Вклад области интегрирования, в которой это разложение справедливо, очень мал. Ограничимся в разложении первым неисчезающим членом.
под знаком интеграла можно разложить в ряд Тейлора в окрестности нуля. Ошибка будет очень мала. Вклад области интегрирования, в которой это разложение справедливо, очень мал. Ограничимся в разложении первым неисчезающим членом.
 . (33)
. (33)
Интеграл  (табличный).
(табличный).
Таким образом,
 . (34)
. (34)
Соответственно, уравнение для химического потенциала принимает вид
 . (35)
. (35)
отсюда
 . (36)
. (36)
Поскольку 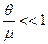 , то будем решать уравнение (105) методом последовательных приближений.
, то будем решать уравнение (105) методом последовательных приближений.
В нулевой приближении
 . (37)
. (37)
В первом приближении
 . (38)
. (38)
Ограничимся этой точностью.
Проведя разложение (107) по малому параметру 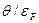 с точностью до линейного члена, находим
с точностью до линейного члена, находим
В результате получаем зависимость хим. потенциала вырожденного электронного газа от температуры
 . (39)
. (39)
Внутренняя энергия вырожденного электронного газа
 . (40)
. (40)
Нас интересует первая неисчезающая поправка по температуре. Поэтому
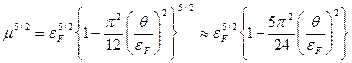 . (41)
. (41)
 . (42)
. (42)
 .(43)
.(43)
Таким образом,
 . (44)
. (44)
Соответственно, теплоемкость вырожденного электронного газа
 . (45)
. (45)