Два разложения для зависимой переменной

Парный регрессионный анализ

Y_i=β₁+β₂X_i+U_i – модель парной линейной регрессии

Β₁,β₂ - константы (параметры уравнения);

X_i – значение объясняющей переменной в наблюдении i;

U_i – случайный член.

Регрессия по методу наименьших квадратов

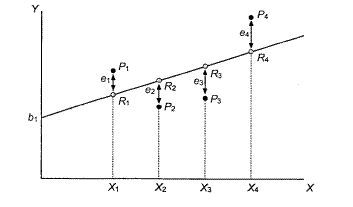
Ŷ=b₁+b₂X_i

Ŷ – оцененное значение Y в зависимости от X;

b₁ – оценка β₁; b₂ – угловой коэффициент прямой (оценка β₂);

R₁-R₄ – теоретические точки;

Необходимо определить, что понимается под остатком

e_i=Y_i-Ŷ_i, т.к. Ŷ=b₁+b₂X_i → e_i=Y_i-b₁-b₂X_i

значит, остаток в каждом наблюдении зависит от нашего выбора значений b₁ и b₂.

Очевидно, что мы хотим построить линию регрессии, т.е. выбрать значения b₁ и b₂ таким образом, чтобы эти остатки были минимальными.

Один из способов состоит в минимизации RSS (суммы квадратов остатков)

RSS=e²₁+e²₂+e²₃+e²₄ (чем меньше RSS, тем больше соответствие) т.е.

RSS=∑e²_i

Алгоритм построения

1. Запишем истинную модель Y_i=β₁+β₂X_i+U_i;

2. Запишем модель оценки для каждого i-го наблюдения Ŷ_i=b₁+b₂X_i;

3. Находим остатки e_i для каждого i-го наблюдения e_i=Y_i-Ŷ_i=Y_i-b₁-b₂X_i;

4. Упрощаем RSS;

5. Необходимо выбрать такие значения b₁ и b₂, чтобы значение RSS было минимальным т.е. необходимо взять частные производные и приравнять их к нулю(необходимые условия первого порядка для минимума) ∂RSS/∂b₁=, ∂RSS/∂b₂=0

6. Итог - получаем уравнение линейной регрессии.

Регрессия по методу наименьших квадратов с одной независимой переменной.

Рассмотрим случай, когда имеется n наблюдений двух переменных X и Y, предположив, что Y зависит от Х.

Можно обнаружить, что RSS минимальна, когда

b₁=Y_ср-b₂X_ср; b₂=(∑(X_i-X_ср)*(Y_i-Y_ср))/∑(X_i-X_ср)²

Два разложения для зависимой переменной

Y=β₁+β₂X – реальное значение, нам не известное;

Y=b₁+b₂X – наша оценка;

т.е. Y=β₁+β₂X_i+U_i – разложение чисто теоретическое (не стохастическая составляющая QT и случайный член PQ);

Y_i=Ŷ_i+e_i=b₁+b₂X_i+e_i – разложение относящееся к линии регрессии.

Y=β₁+β₂X

Ŷ=b₁+b₂X

RT – расчетное значение;

PR – остаток.

Качество оценивания: коэффициент R²

Цель регрессионного анализа состоит в объяснении поведения зависимой переменной Y. Разброс значений Y в любой выборке можно суммарно описать с помощью ∑(Y_i-Y_ср)², суммы квадратов отклонений от выборочного среднего.

∑(Y_i-Y_ср)²=∑(Ŷ_i-Ŷ_ср)²+∑e²_i таким образом TSS=ESS+RSS

TSS – общая сумма квадратов (дана в левой части уравнения);

ESS – «объясненная» сумма квадратов (слагаемое в правой части);

RSS – остаточная («необъясненная») сумма квадратов (слагаемое в правой части).

Замечание – было бы более правильно использовать выражение «видимое объяснение» вместо «объяснение».

R²=∑(Ŷ_i-Ŷ_ср)²/∑(Y_i-Y_ср)² – это часть общей суммы квадратов, объясненной уравнением регрессии. Это соотношение известно как коэффициент детерминации и его обычно обозначают как R².

Максимально возможное значение R²=1. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, так что Ŷ_i=Y_i для всех наблюдений и все остатки равны 0.

Тогда ∑(Ŷ_i-Ŷ_ср)²=/∑(Y_i-Y_ср)², ∑e²_i=0 – идеальное уравнение.

Если в выборке отсутствует видимая связь между Y и X, то R² будет близок к нулю.

При прочих равных условиях желательно, чтобы R² был как можно больше.

В частности, мы заинтересованы в таком выборе коэффициентов b₁ и b₂, чтобы максимизировать R² и при этом b₁ и b₂ должны быть выбраны таким образом, чтобы минимизировать сумму квадратов остатков. Легко показать, что эти критерии эквивалентны

R²=1-(∑e²_i/∑(Y_i-Y_ср)²)

Так же R² фактически равен квадрату коэффициента корреляции r_Y,Ŷ.

r_Y,Ŷ=√ R²