Проблема пятого постулата Евклида. Неевклидовы геометрии
Определения
1. Неевклидова геометрия - буквально, это любая геометрическая система, которая отличается от геометрии Евклида. Например, геометрия Лобачевского, сферическая геометрия, геометрия Римана, проективная геометрия (геометрия Евклида + понятие бесконечно удаленной точки и др.), недезаргова геометрия (в которой теорема Дезарга может не иметь места), неархимедова геометрия. Традиционно термин “неевклидова геометрия” применяется в более узком смысле и относится к двум геометрическим системам: геометрии Лобачевского (гиперболической геометрии) и геометрии Римана (эллиптической геометрии).
2. Геометрия Евклида, геометрия Римана (эллиптическая геометрия) и геометрия Лобачевского (гиперболическая геометрия) формируют 3 великие геометрии.
Аксиомы геометрии Евклида
Евклид в своей геометрии на плоскости дал 5 основных аксиом (потом их изменяли и дополняли, но у Евклида было 5):
1. От всякой точки до всякой точки можно провести прямую. Современная формулировка - через 2 любые точки на плоскости можно провести прямую, и притом только одну.
2. Ограниченную прямую можно непрерывно продолжать по прямой. Современная формулировка: для любых трех точек прямой одна и только одна лежит между двумя другими.
3. Из всякого центра всяким раствором может быть описан круг.
4. Все прямые углы равны между собой.
5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых. Современная формулировка: через точку, не лежащую на прямой, можно провести единственную прямую, параллельную данной.
Геометрия Лобачевского
Геометрия Лобачевского отрицает пятый постулат Евклида. В ней он звучит следующим образом: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. Лобачевский в своей работе “О началах геометрии” (1829) заявил, что пятый постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную и свободную от противоречий, как и евклидова. Одновременно к таким выводам пришли Я. Бойяи и К. Гаусс.
Геометрия Римана
Риман в 1854 г. заметил, что из неограниченности пространства не следует его бесконечная протяженность. У Римана прямые - это большие окружности. Если перемещаться по прямой, то точка в конце концов вернется в исходное положение. Луч OP не имеет предельного положения. Геометрия Римана была известна ещё до геометрии Лобачевского (в частности, засчет её связи со сферической геометрией). Роль прямых на сфере играют окружности. Здесь сумма углов треугольника больше суммы двух прямых. В геометрии Римана любые две прямые имеют общую точку.
Философское значение неевклидовой геометрии
Нельзя абсолютизировать представления о пространстве, и только практика может показать, какое же на самом деле физическое пространство
Немецкий философ Иммануил Кант (1724 – 1804), родоначальник немецкого классического идеализма утверждал, что человек упорядочивает явления реального мира согласно априорным представлениям. Под априорными представлениями Кант понимал идеи, которые врожденны человеческому уму, т.е. раз и навсегда зафиксированы в человеческом разуме, а не зависят от практики или опыта. Геометрические идеи и представления Кант считал априорными. Поэтому Кант, да и многие другие считали, что Евклидова геометрия является непоколебимой вечной истиной. Открытие неевклидовых геометрий показало, что Евклидова геометрия не является единственно возможной. Итак, в основе геометрии лежат не априорные, врожденные уму понятия и аксиомы, а такие понятия, которые связаны с деятельностью человека, с человеческой практикой. Только практика может решить вопрос о том, какая геометрия - вернее излагает свойства физического пространства.
Таким образом, неевклидовы геометрии разрушили идеалистические представления, восходящие ещё к Платону, о том, что геометрия является умозрительной наукой, которая исходит из очевидных аксиом и безукоризненно строго приходит к более достоверным и точным знаниям о мире, чем это может дать эксперимент. Мы не можем точно измерить стороны треугольника, и лишь теоретически можно вывести, что гипотенуза равна сумме квадратов катетов. Т.е. по Платону, логические рассуждения и строгая дедукция - это более строгий метод познания мира. Но неевклидовы геометрии показали, что возможны разные системы аксиом, причем в одной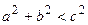 
(геометрия Лобачевского), в другой - 
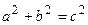(геометрия Евклида) и 
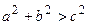(геометрия Римана). То же самое касается суммы углов треугольника (у Лобачевского меньше 180 градусов, у Евклида – равна, у Римана – меньше). И только практика может установить, что же на самом деле истинно. Речь, конечно, не о том, что надо бегать измерять стороны треугольников (погрешности очень малы, мы их не заметим). Однако если будет установлена плотность масс в наблюдаемой части Вселенной, то мы установим, что реально соответствует истине. Общая теория относительности провозгласила, что геометрия нашего мира является неевклидовой, и кривизна пространства зависит от средней плотности масс наблюдаемого вещества во Вселенной. Другое дело, что в нашей повседневной жизни, как правило Евклидовой геометрии достаточно для описания систем и явлений, с которыми мы сталкиваемся в повседневной жизни.