ЦЕНТРАЛЬНЫЙ ФИЛИАЛ
 |
Кафедра правовой информатики, информационного права
И естественнонаучных дисциплин
Утверждаю
Зам. директора по учебной
и воспитательной работе
к.в.н., доцент
В.Д. Ерёменко
31 августа 2011 г.
ПЛАН
Практического занятия
Дисциплина: «Информационные технологии в юридической деятельности».
Тема 4.2: «Общие сведения о системах счисления».
Разработал:
заведующий кафедрой
к.т.н., доцент
А.В. Мишин
Материалы обсуждены и одобрены
на заседании кафедры ПИИПЕД,
протокол № 1 от «29 » августа 2011 г.
Воронеж - 2011
План проведения занятия
Тема № 4: «Основные закономерности создания информационных процессов».
Занятие № 2: «Общие сведения о системах счисления».
| Учебные вопросы | Время, мин |
| Вступительная часть.................................... 1. Понятие системы счисления............................. 2. Перевод чисел из одной системы счисления в другую....... Заключительная часть................................... |
Литература:
основная:
1. Мишин А.В. Информатика и математика: математика: учеб. пособие / А.В. Мишин, Л.Е. Мистров, А.Ю. Кузьмин. – Воронеж: Научная книга, 2006. – С. 9-14.
дополнительная:
2. Горбатов В.А. Дискретная математика: Учебник / В.А. Горбатов, А.В. Горбатов, М.В. Горбатова. – М.: ООО «Издательство АСТ»: ООО «Издательство Астрель», 2003. – С. 43-56.
Содержание занятия и методика его проведения
Вступительная часть. Преподаватель проверяет наличие и готовность студентов к проведению занятия, делает соответствующие записи в журнале. Объявляется тема, цель и план проведения занятия. Акцентируется внимание студентов на важности изучаемой темы для усвоения последующего материала учебной дисциплины.
Основная часть. Преподаватель проверяет усвоение студентами ранее изученного учебного материала и выполнение ими домашнего задания.
1. Для множеств 
и 
: А È В = {-10, -3, -2, -1, 0, 4, 5, 8}. А Ç В = {4, 8}. В \ А = {-3, -1, 0}. A D B = {-10, -3, -2, -1, 0, 5}.
2. Для множеств A = {2, 4} и B ={1, 5, 7}: 
= {(2, 1), (2, 5), (2, 7), (4, 1), (4, 5), (4, 7)}.
3. Диаграммы Эйлера-Венна множеств:
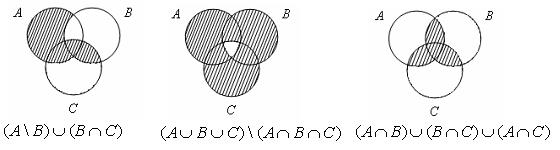
Доводит основные теоретические сведения и организует выполнение заданий по теме.
Заключительная часть. В заключительной части практического занятия преподаватель подводит итоги, отмечает ошибки в действиях студентов, оценивает работу и отвечает на их вопросы, выдаёт задание на самоподготовку.
Задача. Найти результат вычисления выражения 
.
Тема 4.2. Общие сведения о системах счисления
Цель занятия – изучить первичные понятия представления чисел в позиционных системах счисления, необходимые для последующего восприятия закономерностей создания информационных процессов.
Теоретические сведения
Понятие системы счисления
Системой счисления (или нумерацией) называют совокупность приёмов построения, обозначения и наименования чисел. Каждая система счисления включает:
1) определённый набор символов (цифр) для записи чисел; эти символы составляют конечный алфавит;
2) определённый способ чтения (наименования) чисел.
Каждой цифре в записи числа однозначно сопоставляется количество, выражаемое этой цифрой. Это количество будем называть количественным эквивалентом цифры [1].
По способу определения количественного эквивалента цифры в записи числа все системы счисления можно разбить на два класса: непозиционные и позиционные.
Система счисления называется непозиционной, если каждой цифре и в любом месте в записи числа однозначным образом сопоставлен некоторый количественный эквивалент. Таким образом, в непозиционных системах счисления местоположение цифры в записи числа (позиция) не влияет на её количественный эквивалент.
Примером непозиционной системы счисления является римская система[2]. Количественные эквиваленты цифр римской системы счисления равны: (I) = l; (V) = 5; (X) = 10; (L) = 50; (С) = 100; (D) = 500; (М) = 1000.
Количественный эквивалент числа в римской системе счисления определяется по следующему правилу: если в записи числа слева от символа находится символ, имеющий не меньший количественный эквивалент, то этот количественный эквивалент включается в сумму со знаком «плюс», в противном случае - со знаком «минус». Например,количественные эквиваленты чисел CCXXXIX и DCCXL равны: …….(CCXXXIX) = 10 - 1 + 10 + 10 + 10 + 100 + 100 = 239,
(DCCXL) = 50 –10 + 100 + 100 + 500 = 740.
Исторически вначале появились непозиционные системы счисления. Общим недостатком этих систем счисления является трудность записи в них больших чисел: либо эти записи слишком громоздки, либо алфавит цифр весьма велик. Именно поэтому непозиционные системы счисления в вычислительной технике практически не нашли применения.
Система счисления называется позиционной, если количественный эквивалент цифры определяется не только видом самой цифры, но и её местоположением в записи числа - позицией.
Примером такой системы является широко используемая нами десятичная система. При смене позиции (места) цифры в числе меняется её количественный эквивалент. Например, у числа 333,3 первая цифра справа означает «три десятых долей единицы», вторая «три единицы», третья – «три десятка», а четвёртая – «три сотни». Сама же запись 333,3 означает сокращённую запись выражения 300 + 30 + + 3 + 0,3 = 3×102 + 3×101 + 3×100 + 3×10 –1 = 333,3.
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления – это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание системы можно принять любое натуральное число – два, три, четыре и т.д.
Наиболее широкое использование имеют следующие системы счисления:
· десятичная (используются цифры 0, 1, 2,..., 9);
· двоичная (используются цифры 0, 1);
· восьмеричная (используются цифры 0, 1, 2,..., 7);
· шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, 2,..., 9, а для следующих чисел – от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).
Любое число А в позиционной системе счисления можно записать в общем виде [3]:
А ( p ) = 
,
где ai – цифра в i -том разряде записи числа в системе счисления с основанием р.
Для определения номера разряда (значения i) используется простое правило (см. рис. 4.7): первый слева от запятой разряд (точка отсчёта) является нулевым; номера остальных разрядов равны их порядковому номеру относительно нулевого разряда: влево (целая часть числа) – со знаком «+» (при записи опускается); вправо (дробная часть числа) – со знаком «–». Например,
324,54(10) = 3×102 + 2×101 + 4×100 + 5×10–1 + 4×10–2,
1101,01(2) = 1×23 + 1×22 + 0×21 +1×20 + 0×2–1 + 1×2–2,
352,51(8) = 3×82 + 5×81 + 2×80 + 5×8-1 + 1×8–2,
A4C,3F(16) = 10×162 + 4×161 + 12×160 + 3×16–1 + 15×16–2.
Рис. 4.7. Принцип нумерации разрядов записи числа