Окружность и ее свойства

3.1 Общие сведения

Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.

Данная точка называется центром окружности.

Круг – часть плоскости, ограниченная окружностью.

Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом окружности.

Отрезок, соединяющий две точки окружности, называется хордой.

Хорда, проходящая через центр окружности, называется диаметром окружности.

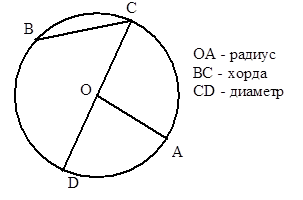
Прямая, имеющая с окружностью две общие точки, называется секущей.

Прямая, имеющая с окружностью одну общую точку, называется касательной.

Отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей (число «пи», ).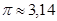

Длина окружности: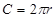

Длина дуги окружности: .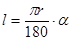

Площадь круга: .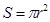

Круговым сектором (сектор) называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Круговым сегментом называется часть круга, ограниченная дугой и хордой, соединяющей концы этой дуги.

Площадь сектора: .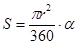

Центральный угол – угол, вершина которого центр окружности, а стороны пересекают эту окружность.

Вписанный угол – угол, вершина которого лежите на окружности, а стороны пересекают эту окружность.

3.2 Свойства окружности и ее элементов (хорд, касательных, секущих, вписанных и центральных углов)
Если диаметр окружности перпендикулярен хорде, то точка пересечения – середина этой хорды. Обратно: Если диаметр пересекает хорду в ее середине, то он перпендикулярен этой хорде.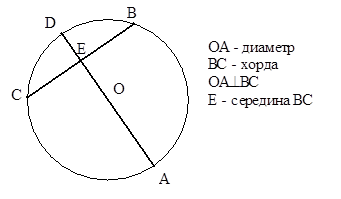
Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.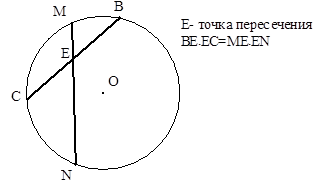
Дуги, заключенный между параллельными хордами равны.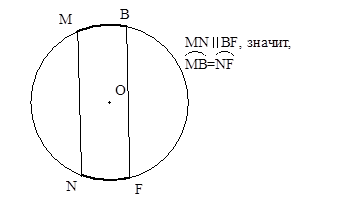
Центральный угол измеряется дугой, на которую он опирается.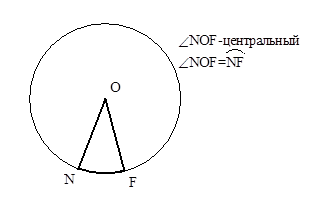
Вписанный угол измеряется половиной дуги, на которую он опирается.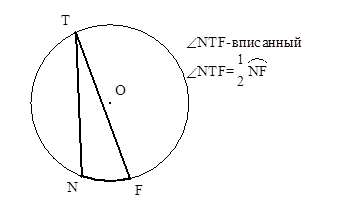
Вписанные углы, опирающиеся на одну и ту же дугу, равны.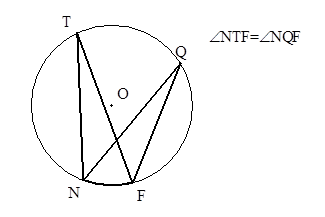
Вписанный угол, опирающийся на полуокружность (на диаметр), прямой.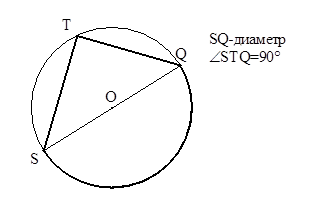
Угол, между пересекающимися хордами равен полусумме дуг, заключенных между ними.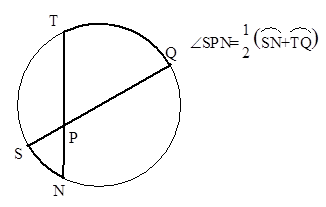
Угол, между секущими равен полуразности дуг, заключенных между ними.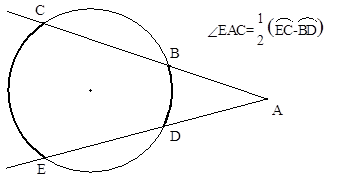
Угол между касательной и секущей, проведенных из одной точки к данной окружности, равен половине дуги, заключенной между ними.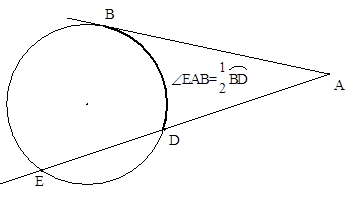
Угол между касательной и хордой, проведенной из точки касания, равен половине дуги, заключенной между ними.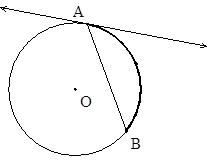
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.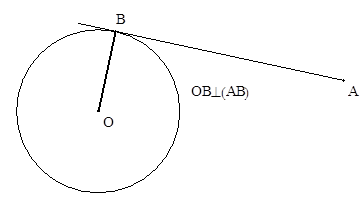
Отрезки касательных, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.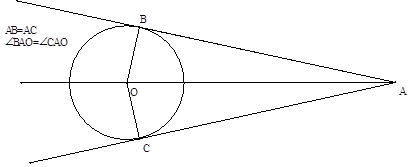
Если из точки, не лежащей на данной окружности, провести две секущие, то произведение отрезка секущей и ее внешней части, будет равно произведению отрезка другой секущей на ее внешнюю часть.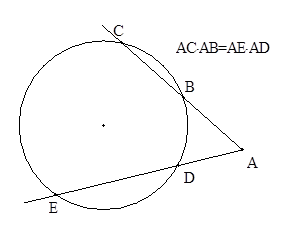
Квадрат отрезка касательной равен произведению отрезка секущей, проведенной из той же точки, что и касательная, на ее внешнюю часть.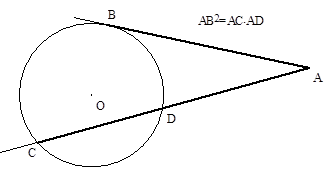

3.3 Касание и пересечение окружностей

Внешнее касание	Внутреннее касание
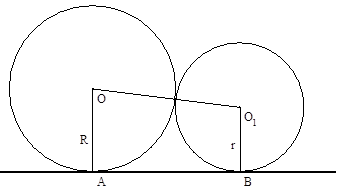
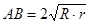АВ – внешняя касательная (окружности располагаются по одну сторону от касательной)
Центры касающихся окружностей и точка касания окружностей лежат на одной прямой.
Пересечение окружностей, когда общая хорда лежит между их центрами.	Пересечение окружностей, когда общая хорда не лежит между их центрами.

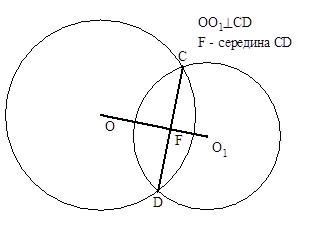
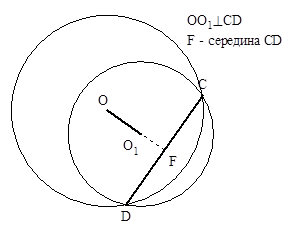
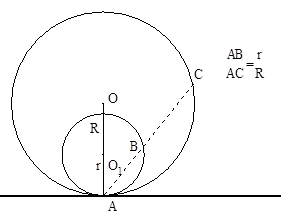
Векторы и координаты

Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором.

Ненулевые векторы коллинеарны, если они лежат на одной прямой или на параллельных прямых.

Векторы равны, если они сонаправлены, и длины их равны.

От любой точки плоскости можно отложить вектор равный данному и притом только один.

Если ненулевые векторы 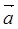и 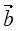коллинеарны, то существует, отличное от нуля число k, что .

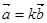Суммой векторов 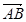и 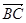является вектор .

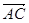Любой вектор 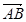можно представить как разность двух векторов с заданным началом, например, M: .

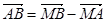Для любых чисел m, n и любых векторов 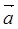и 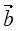справедливы равенства:

· ,

· ,

· .

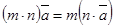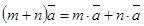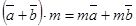Если С – середина отрезка АВ, и О – произвольная точка, то .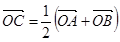

Если С – делит отрезок АВ, в отношении m: n, считая от точки А, то для любой точки О справедливо равенство .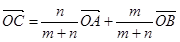

Любой вектор можно разложить единственным образом по двум данным неколлинеарным векторам: .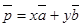

Есл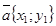и и ,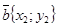

· ,

· ,

· ,

· ,

· ,

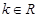
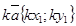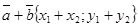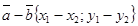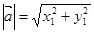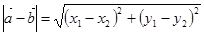Скалярное произведение векторов

· ,

· ,

· .

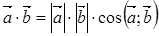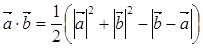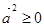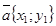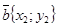· Если и , то .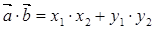

Середина отрезка АВ, где А (х₁;у₁) и В (х₂;у₂), имеет координаты .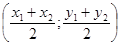

Множество точек (х;у), координаты которых удовлетворяют уравнению 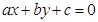(a и b не равны нулю одновременно), есть прямая. (Уравнение прямой: ).

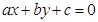Уравнение прямой, проходящей через две точки: .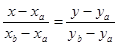

Угол 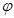между двумя прямыми :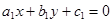

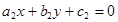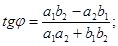
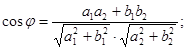
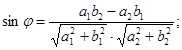
(Угол 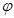отсчитывается от первой прямой ко второй, против часовой стрелки).

Если 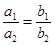, то прямые параллельны.

Если 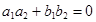, то прямые перпендикулярны.

Расстояние от точки А (х₀;у₀) до прямой l, задаваемой уравнением 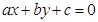, равно .

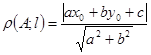Если 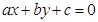уравнение некоторой прямой, то вектор с координатами (a;b) перпендикулярен этой прямой.

Множество точек (х;у), координаты которых удовлетворяют уравнению 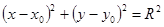, есть окружность с центром в точке (х₀;у₀) и радиусом R (Уравнение окружности: ).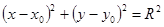