Шкала наименований
Собственно измерений, отвечающих определению этого действия, в шкале наименований не производится. Здесь речь идет о группировке объектов, идентичных по определенному признаку,и о присвоении им обозначений. Не случайно, что другое название этой шкалы—номинальное (от латинского слова nome — имя).
Обозначениями, присваиваемыми объектам, являются числа. Например, легкоатлеты-прыгуны в длину в этой шкале могут обозначаться номером 1, прыгуны в высоту — 2, прыгуны тройным — 3,прыгуны с шестом — 4.
При номинальных измерениях вводимая символика означает,что объект 1 только отличается от объектов 2, 3 или 4. Однако насколько отличается и в чем именно, по этой шкале измерить нельзя.
Шкала порядка
Если какие-то объекты обладают определенным качеством, то порядковые измерения позволяют ответить на вопрос о различиях в этом качестве. Например, соревнования в беге на 100 м — это
определение уровня развития скоростно-силовых качеств. У спортсмена, выигравшего забег, уровень этих качеств в данный момент выше, чем у пришедшего вторым. У второго, в свою очередь, выше, чем у третьего, и т. д.
Но чаще всего шкала порядка используется там, где невозможны качественные измерения в принятой системе единиц.
При использовании этой шкалы можно складывать и вычитать ранги или производить над ними какие-либо другие математические действия.
Шкала интервалов
Измерения в этой шкале не только упорядочены по рангу, но и разделены определенными интервалами. В интервальной шкале установлены единицы измерения (градус, секунда, и т. д.). Измеряемому объекту здесь присваивается число, равное количеству единиц измерения, которое он содержит.
Здесь можно использовать любые методы статистики, кроме определения отношений. Связано это с тем, что нулевая точка этой шкалы выбирается произвольно.
Шкала отношений
В шкале отношений нулевая точка не произвольна, и, следовательно, в некоторый момент времени измеряемое качество может быть равно нулю. В связи с этим при оценке результатов измерений в этой шкале возможно определить «во сколько раз» один объект больше другого.
В этой шкале какая-нибудь из единиц измерения принимается за эталон, а измеряемая величина содержит столько этих единиц, во сколько раз она больше эталона. Результаты измерений в этой шкале могут обрабатываться любыми методами математической статистики.
Основные единицы СИ Единица
Величина Размерность Название Обозначение
русское международное
Длина L Метр м m
Масса M Килограмм кг kg
Время T Секунда с S
Сила эл. тока Ампер А A
Температура Кельвин К K
Кол-во вещ-ва Моль моль mol
Сила света Канделла Кд cd
3.Точность измерений. Погрешности и их разновидности и методы устранения.
Никакое измерение не может быть выполнено абсолютно точно. Результат измерения неизбежно содержит погрешность, величина которой тем меньше, чем точнее метод измерения и измерительный прибор.
Основная погрешность — это погрешность метода измерения или измерительного прибора, которая имеет место в нормальных условиях их применения.
Дополнительная погрешность — это погрешность измерительного прибора, вызванная отклонением условий его работы от нормальных.
Величина D А=А-А0, равная разности между показанием измерительного прибора (А) и истинным значением измеряемой величины (А0), называется абсолютной погрешностью измерения. Она измеряется в тех же единицах, что и сама измеряемая величина.
Относительная погрешность — это отношение абсолютной погрешности к значению измеряемой величины:
Систематической называется погрешность, величина которой не меняется от измерения к измерению. В силу этой своей особенности систематическая погрешность часто может быть предсказана заранее или в крайнем случае обнаружена и устранена по окончании процесса измерения.
Тарированием (от нем. tarieren) называется проверка показаний измерительных приборов путем сравнения с показаниями образцовых значений мер (эталонов*) во всем диапазоне возможных значений измеряемой величины.
Калибровкой называется определение погрешностей или поправка для совокупности мер (например, набора динамометров). И при тарировании, и при калибровке к входу измерительной системы вместо спортсмена подключается источник эталонного сигнала известной величины.
Рандомизацией (от англ. random — случайный) называется превращение систематической погрешности в случайную. Этот прием направлен на устранение неизвестных систематических погрешностей. По методу рандомизации измерение изучаемой величины производится несколько раз. При этом измерения организуют так, чтобы постоянный фактор, влияющий на их результат, действовал в каждом случае по-разному. Скажем, при исследовании физической работоспособности можно рекомендовать измерять ее многократно, всякий раз меняя способ задания нагрузки. По окончании всех измерений их результаты усредняются по правилам математической статистики.
Случайные погрешности возникают под действием разнообразных факторов, которые ни предсказать заранее, ни точно учесть не удается.
4.Основы теории вероятностей. Случайное событие, случайная величина, вероятность.
Теория вероятностей - теорию вероятностей можно определить как раздел математики, в котором изучаются закономерности, присущие массовым случайным явлениям.
Условная вероятность - условной вероятностью РА(В) события В называется вероятность события В, найденная в предположении, что событие А уже наступило.
Элементарное событие - события U1, U2,..., Un, образующие полную группу попарно несовместимых и равновозможных событий, будем называть элементарными событиями.
Случайное событие - событие называется случайным, если оно объективно может наступить или не наступить в данном испытании.
Событие - результат (исход) испытания называется событием.
Любое случайное событие обладает какой-то степенью воз-можности, которую в принципе можно измерить численно. Что-бы сравнивать события по степени их возможности, нужно связать с каждым из них какое-то число, которое тем боль-ше, чем больше возможность события. Это число мы и назовем вероятностью события.
Характеризуя вероятности событий числами, нужно устано-вить какую-то единицу измерения. В качестве такой единицы естественно взять вероятность достоверного события, т.е. такого события, которое в результате опыта неизбежно долж-но произойти.
Вероятность какого либо события – численное выражение возможности его наступления.
В некоторых простейших случаях вероятности событий могут быть легко определены непосредственно исходя из условий испытаний.
Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.
5.Генеральная и выборочная совокупности. Объем выборки. Неупорядоченная и ранжированная выборки.
В выборочном наблюдении используются понятия «генеральная совокупность» -- изучаемая совокупность единиц, подлежащая изучению по интересующим исследователя признакам, и «выборочная совокупность» -- случайно выбранная из генеральной совокупности некоторая ее часть. К данной выборке предъявляется требование репрезентативности, т.е. при изучении лишь части генеральной совокупности полученные выводы можно применять ко всей совокупности.
Характеристиками генеральной и выборочной совокупностей могут служить средние значения изучаемых признаков, их дисперсии и средние квадратические отклонения, мода и медиана и др. Исследователя могут интересовать и распределение единиц по изучаемым признакам в генеральной и выборочной совокупностях. В этом случае частоты называются соответственно генеральными и выборочными.
Система правил отбора и способов характеристики единиц изучаемой совокупности составляет содержание выборочного метода, суть которого состоит в получении первичных данных при наблюдении выборки с последующим обобщением, анализом и их распространением на всю генеральную совокупность с целью получения достоверной информации об исследуемом явлении.
Репрезентативность выборки обеспечивается соблюдением принципа случайности отбора объектов совокупности в выборку. Если совокупность является качественно однородной, то принцип случайности реализуется простым случайным отбором объектов выборки. Простым случайным отбором называют такую процедуру образования выборки, которая обеспечивает для каждой единицы совокупности одинаковую вероятность быть выбранной для наблюдения для любой выборки заданного объема. Таким образом, цель выборочного метода -- сделать вывод о значении признаков генеральной совокупности на основе информации случайной выборки из этой совокупности.
Объем выборки - в аудите - количество единиц, отбираемых аудитором из проверяемой совокупности.
Выборка называется неупорядоченной, если порядок следования элементов в ней не существенен.
6.Основные статистические характеристики положения центра ряда.
Показатели положения центра распределения. К ним относятся степенная средняя в виде средней арифметической и структурные средние – мода и медиана.
Средняя арфметическая для дискретного ряда распределения рассчитывается по формуле:

В отличие от средней арифметической, рассчитываемой на основе всех вариант, мода и медиана характеризует значение признака у статистической единице, занимающей определенное положение в вариационном ряду.
Медиана ( Me ) - значение признака у статистической единицы, стоящей в середине ранжированного ряда и делящей совокупность на две равные по численности части.
Мода (Mo) - наиболее часто встречаемое значение признак в совокупности. Мода широко используется в статистической практике приизучении покупательского спроса, регистрации цен и др.
Для дискретных вариационных рядов Mo и Me выбираются в соответствии с определениями: мода - как значение признака с наибольшей частотой  : положение медианы при нечетном объеме совокупности определяется ее номером
: положение медианы при нечетном объеме совокупности определяется ее номером  , где N – объем статистической совокупности. При четном объеме ряда медиана равна средней из двух вариантов, находящихся в середине ряда.
, где N – объем статистической совокупности. При четном объеме ряда медиана равна средней из двух вариантов, находящихся в середине ряда.
Медиану используют как наиболее надежный показатель типичного значения неоднородной совокупности, так как она нечувствительна ккрайним значениям признака, которые могут значительно отличаться отосновного массива его значений. Кроме этого, медиана находитпрактическое применение вследствие особого математического свойства:  Рассмотрим определение моды и медианы на следующем примере:имеется ряд распределения рабочих участка по уровню квалификации.
Рассмотрим определение моды и медианы на следующем примере:имеется ряд распределения рабочих участка по уровню квалификации.
7.Основные статистические характеристики рассеивания (вариации).
Однородность статистических совокупностей характеризуется величиной вариации (рассеяния) признака, т.е. несовпадением его значений у разных статистических единиц. Для измерения вариации в статистике используются абсолютные и относительные показатели.
К абсолютным показателям вариации относятся:
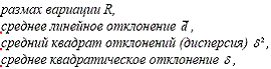
Размах вариации R является наиболее простым показателем вариации: 
Этот показатель представляет собой разность между максимальным и минимальным значениями признаков и характеризует разброс элементов совокупности. Размах улавливает только крайние значения признака в совокупности, не учитывает повторяемость его промежуточных значений, а также не отражает отклонений всех вариантов значений признака.
Размах часто используется в практической деятельности, например, различие между max и min пенсией, заработной платой в различных отраслях и т.д.
Среднее линейное отклонение d является более строгой характеристикой вариации признака, учитывающей различия всех единиц изучаемой совокупности. Среднее линейное отклонение представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической. Этот показатель рассчитывается по формулам простой и взвешенной средней арифметической:

В практических расчетах среднее линейное отклонение используется для оценки ритмичности производства, равномерности поставок. Так как модули обладают плохими математическими свойствами, то на практике часто применяют другие показатели среднего отклонения от средней – дисперсию и среднее квадратическое отклонение.
Среднее квадратическое отклонение представляет собой среднюю квадратическую из отклонений отдельных значений признака от их средней арифметической:

8.Достоверность различий статистических показателей.
В статистике величину называют статисти́чески зна́чимой, если вероятность её случайного возникновения мала, то есть нулевая гипотеза может быть отклонена. Разница называется «статистически значимой», если имеются данные, появление которых было бы маловероятно, если предположить, что эта разница отсутствует; это выражение не означает, что данная разница должна быть велика, важна, или значима в общем смысле этого слова.
9.Графическое изображение вариационных рядов. Полигон и гистограмма распределения.
Графики являются наглядной формой отображения рядов распределения. Для изображения рядов применяются линейные графики и плоскостные диаграммы, построенные в прямоугольной системе координат.
Для графического представления атрибутивных рядов распределения используются различные диаграммы: столбиковые, линейные, круговые, фигурные, секторные и т. д.
Для дискретных вариационных рядов графиком является полигон распределения.
Полигоном распределения называется ломаная линия, соединяющая точки с координатами или где - дискретное значение признака, - частота, - частость. Полигон применяют для графического изображения дискретного вариационного ряда, и этот график является разновидностью статистических ломаных. В прямоугольной системе координат по оси абсцисс откладываются варианты признака, а по оси ординат – частости каждого варианта. На пересечении абсциссы и ординаты фиксируют точки, соответствующие данному ряду распределения. Соединив эти точки прямыми, получим ломаную, которая и является полигоном, или эмпирической кривой распределения. Для замыкания полигона крайние вершины соединяют с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе, или с серединами предыдущего (перед начальным) и последующим (за последним) интервалов.
Для изображения интервальных вариационных рядов применяют гистограммы, представляющие собой ступенчатые фигуры, состоящие из прямоугольников, основания которых равны ширине интервала, а высота - частоте (частости) равноинтервального ряда или плотности распределения неравноинтервального Построение диаграммы аналогично построению столбиковой диаграммы Гистограмма применяется для графического изображения непрерывных (интервальных) вариационных рядов. При этом на оси абсцисс откладывают интервалы ряда. На этих отрезках строят прямоугольники, высота которых по оси ординат в принятом масштабе соответствует частотам. При равных интервалах по оси абсцисс откладывают прямоугольники, сомкнутые друг с другом, с равными основаниями и ординатами, пропорциональными весам. Данный ступенчатый многоугольник и называется гистограммой. Его построение аналогично построению столбиковых диаграмм. Гистограмма может быть преобразована в полигон распределения, для чего середины верхних сторон прямоугольников соединяют отрезками прямых. Две крайние точки прямоугольников замыкают по оси абсцисс на середине интервалов аналогично замыканию полигона. В случае неравенства интервалов график строится не по частотам или частостям, а по плотности распределения (отношению частот или частостей к величине интервала), и тогда высоты прямоугольников графика будут соответствовать величинам этой плотности.
При построении графиков рядов распределения большое значение имеет соотношение масштабов по оси абсцисс и оси ординат. В этом случае и необходимо руководствоваться «правилом золотого сечения», в соответствии с которым высота графика должна быть примерно в два раза меньше его основания
10.Нормальный закон распределения (сущность, значение). Кривая нормального распределения и ее свойства. https://igriki.narod.ru/index.files/16001.GIF
Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равна
,
где m - математическое ожидание случайной величины;
σ2 - дисперсия случайной величины, характеристика рассеяния значений случайной величины около математического ожидания.
Условием возникновения нормального распределения являются формирование признака как суммы большого числа взаимно независимых слагаемых, ни одно из которых не характеризуется исключительно большой по сравнению с другими дисперсиями.
Нормальное распределение является предельным, к нему приближаются другие распределения.
Математическое ожидание случайной величины Х. распределено по нормальному закону, равно
mx = m, а дисперсия Dx = σ2.
Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервале (α, β) выражается формулой
где - табулированная функция
11.Правило трех сигм и его практическое применение.
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.
Это правило называется правилом трех сигм.
Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
12.Виды статистической взаимосвязи.
Качественный анализ изучаемого явления позволяет выделить основные причинно-следственные связи данного явления, установить факторные и результативные признаки.
Взаимосвязи, изучаемые в статистике, могут быть классифицированы по ряду признаков:
1)По характеру зависимости: функциональные (жесткие), корреляционные (вероятностные)
Функциональные связи – это связи, при которых каждому значению факторного признака соответствует единственное значение результативного признака.
При корреляционных связях отдельному значению факторного признака могут соответствовать разные значения результативного признака.
Такие связи проявляются при большом количестве наблюдений, через изменение средней величины результативного признака под воздействием факторных признаков.
2) По аналитическому выражению: прямолинейные, криволинейные.
3) По направлению: прямые, обратные.
4) По числу факторных признаков, которые оказывают влияние на результативный признак: однофакторные, многофакторные.
Задачи статистического изучения взаимосвязей:
-Установление наличия направления связи;
-количественное измерение влияния факторов;
-измерение тесноты связи;
-оценка достоверности полученных данных.
13.Основные задачи корреляционного анализа.
1. Измерение степени связности двух и более переменных. Наши общие знания об объективно существующих причинных связях должны дополняться научно обоснованными знаниями о количественной мере зависимости между переменными. Данный пункт подразумевает верификацию уже известных связей.
2. Обнаружение неизвестных причинных связей. Корреляционный анализ непосредственно не выявляет причинных связей между переменными, но устанавливает силу этих связей и их значимость. Причинный характер выясняют с помощью логических рассуждений, раскрывающих механизм связей.
3. Отбор факторов, существенно влияющих на признак. Самые важные те факторы, которые сильнее всего коррелируют с изучаемыми признаками.
14.Корреляционное поле. Формы взаимосвязи.
Вспомогательное средство анализа выборочных данных. Если даны значения двух признаков xl... хn и yl... уn, то при составлении К. п. точки с координатами (xl, yl) (хn... уn) наносят на плоскость. Расположение точек позволяет сделать предварительное заключение о характере и форме зависимости.
Для описания причинно-следственной связи между явлениями и процессами используется деление статистических признаков, отражающих отдельные стороны взаимосвязанных явлений, нафакторные и результативные. Факторными считаются признаки, обуславливающие изменение других, связанных с ними признаков,являющихся причинами и условиями таких изменений. Результативными являются признаки, изменяющимися под воздействием факторных.
Формы проявления существующих взаимосвязей весьма разнообразны. В качестве самых общих их видов выделяют функциональную и статистическую связи.
Функциональной называют такую связь, при которой определённому значению факторного признака соответствует одно и только одно значение результативного. Такая связь возможна приусловии, что на поведение одного признака (результативного) влияеттолько второй признак (факторный) и никакие другие.Такие связи являются абстракциями, в реальной жизни онивстречаются редко, но находят широкое применение в точных науках и впервую очередь, в математике. Например: зависимость площади круга отрадиуса: S=π∙ r 2
Функциональная связь проявляется во всех случаях наблюдения и для каждой конкретной единицы изучаемой совокупности. В массовых явлениях проявляются статистические связи, при которых строго определённому значению факторного признака ставится в соответствие множество значений результативного. Такие связиимеют место, если на результативный признак действуют несколькофакторных, а для описания связи используется один или несколькоопределяющих (учтённых) факторов.
Строгое различие между функциональной и статистической связью можно получить при их математической формулировке.
Функциональную связь можно представить уравнением:  вследствие действия неконтролируемых факторов или ошибок измерения.
вследствие действия неконтролируемых факторов или ошибок измерения.
Примером статистической связи может служить зависимость себестоимости единицы продукции от уровня производительности труда: чем выше производительность труда, тем ниже себестоимость. Но на себестоимость единицы продукции помимо производительности труда влияют и другие факторы: стоимость сырья, материалов, топлива, общепроизводственные и общехозяйственные расходы и т.д. Поэтому нельзя утверждать, что изменение производительности труда на 5% (повышение) приведет к аналогичному снижению себестоимости. Может наблюдаться и обратная картина, если на себестоимость будут влиять в бóльшей степени другие факторы, - например, резко возрастут цены на сырье и материалы.
Любую статистическую связь можно представить в виде набора локальных распределений результативного признака при фиксированных значениях факторного.
По форме (аналитическому выражению) связи делятся на линейные (прямолинейные) и нелинейные (криволинейные) связи. Линейные связи выражаются уравнением прямой, а нелинейные – уравнением параболы, гиперболы, степенной и т. п.
15. Методы вычисления коэффициентов взаимосвязи. Вычисление парного линейного коэффициента корреляции Бравэ-Пирсона.
В качестве оценки генерального коэффициента корреляции р используется коэффициент корреляции r Браве-Пирсона. Для его определения принимается предположение о двумерном нормальном распределении генеральной совокупности, из которой получены экспериментальные данные. Это предположение может быть проверено с помощью соответствующих критериев значимости. Следует отметить, что если по отдельности одномерные эмпирические распределения значений xi и yi согласуются с нормальным распределением, то из этого еще не следует, что двумерное распределение будет нормальным. Для такого заключения необходимо еще проверить предположение о линейности связи между случайными величинами Х и Y. Строго говоря, для вычисления коэффициента корреляции достаточно только принять предположение о линейности связи между случайными величинами, и вычисленный коэффициент корреляции будет мерой этой линейной связи.
Коэффициент корреляции Браве-Пирсона () относится к параметрическим коэффициентам и для практических расчетов вычисляется по формуле:
Из формулы видно, что для вычисления необходимо найти средние значения признаков Х и Y, а также отклонения каждого статистического данного от его среднего. Зная эти значения, находятся суммы. Затем, вычислив значение, необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным для f = n -2. Если, то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если, то между признаками наблюдается недостоверная корреляционная взаимосвязь[
16.Вычисление рангового коэффициента корреляции Спирмена.
Коэффициент ранговой корреляции Спирмена (Spearman rank correlation coefficient) — мера линейной связи между случайными величинами. Для оценки силы связи между величиными используются не численные значения, а соответствующие им ранги.
Этот коэффициент определяет степень тесноты и направленность связи признаков. Величина коэффициента лежит в интервале от +1 до -1. Абсолютное значение характеризует тесноту связи, а знак - направленность связи между двумя признаками.
Преимущество
Можно ранжировать по признакам, которые нельзя выразить численно: субъективные оценки, предпочтения и т.д. При экспертных оценках можно ранжировать оценки разных экспертов и найти их корреляции друг с другом, чтобы затем исключить из рассмотрения оценки эксперта, слабо коррелирующие с оценками других. Коэффициент корреляции рангов применяется для оценки устойчивости тенденции динамики.
Недостатки
Недостатком коэффициента корреляции рангов является то, что одинаковым разностям рангов могут соответствовать совершенно отличные разности значений (в случае количественных признаков). Недоучет размеров отклонений признаков от их средних величин занижает меру тесноты связи. Поэтому для количественных признаков корреляция рангов обладает меньшей информативностью, чем коэффициент корреляции числовых значений этих признаков.
Свойства
· инвариантен (не изменен) по отношению к любому монотонному преобразованию шкалы измерения;
· относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале;
· при расчете не требуется никаких предположений о характере распределений признаков в генеральной совокупности.
Коэффициент корреляции рангов Спирмэна (р) основан на рассмотрении разности рангов значений результативного и факторного признаков и может быть рассчитан по формуле
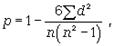
где d = Nx - Ny, т.е. разность рангов каждой пары значений х и у; n - число наблюдений.
17.Статистическая проверка гипотез (цель, сущность), критерии их проверки.
Смысл проверки статистической гипотезы состоит в том, чтобы по имеющимся статистическим данным принять или отклонить статистическую гипотезу с минимальным рисков ошибки. Эта проверка осуществляется по определенным правилам.
Проверка статистических гипотез осуществляется с помощью статистического критерия (назовем его в общем виде К), являющегося функцией от результатов наблюдения.
Статистический критерий – это правило (формула), по которому определяется мера расхождения результатов выборочного наблюдения с высказанной гипотезой Н 0.
Как уже отмечалось выше, следует иметь в виду, что статистическая проверка гипотез имеет вероятностный характер, так как принимаемые вывод основываются на изучении свойств распределения случайной переменной по данным выборки, а потому всегда существует риск допустить ошибку. Однако с помощью статистической проверки гипотез можно определить вероятность принятия ложного решения. Если вероятность последнего невелика, то можно считать, что применяемый критерий обеспечивает малый риск ошибки.
При проведении проверки статистических гипотез в первую очередь приходится решать задачи статистической проверки гипотез о:
1) принадлежности «выделяющихся» единиц исследуемой выборочной совокупности генеральной совокупности;
2) виде распределения изучаемых признаков;
3) величине средней арифметической и доли;
4) наличии и тесноте связи между изучаемыми признаками;
5) о форме корреляционной связи.
18. Понятие об уровне значимости в статистических расчетах.
Значимости уровень статистического критерия, вероятность ошибочно отвергнуть основную проверяемую гипотезу, когда она верна. В теории статистической проверки гипотез Значимости уровень называется вероятностью ошибки первого рода. Понятие «Значимости уровень » возникло в связи с задачей проверки согласованности теории с опытными данными. Если, например, в результате наблюдений регистрируются значения n случайных величин X1,..., Xn и если требуется по этим данным проверить гипотезу Н, согласно которой совместное распределение величин X1,..., Xn обладает некоторым определённым свойством, то соответствующий статистический критерий конструируется с помощью подходящим образом подобранной функции Y = f (X1,..., Xn); эта функция обычно принимает малые значения, когда гипотеза Н верна, и большие значения, когда Н ложна. В частности, если X1,..., Xn — результаты независимых измерений некоторой известной постоянной а и гипотеза Н представляет собой предположение об отсутствии в результатах измерений систематических ошибок, то для проверки Н разумно в качестве Y выбрать (2m — n) 2, где m — количество тех результатов измерений X1, которые превышают истинное значение а. Наблюдаемое в опыте большое значение Y можно рассматривать как значимое статистическое опровержение гипотетического согласия между результатами наблюдений и проверяемой гипотезой. Соответствующий критерий значимости представляет собой правило, согласно которому значимыми считаются значения Y, превосходящие заданное критическое значение у. В свою очередь выбор величины у определяется заданным Значимости уровень, который в случае справедливости гипотезы Н совпадает с вероятностью события { Y > y }.
Уровень значимости - это вероятность того, что мы сочли различия существенными, а они на самом деле случайны.
Если перевести все это на более формализованный язык, то уровень значимости - это вероятность отклонения нулевой гипотезы, в то время как она верна.
В статистике величину называют статистимчески знамчимой, если мала вероятность чисто случайного возникновения её или ещё более крайних величин. Здесь под крайностью понимается степень отклонения от нуль-гипотезы. Разница называется «статистически значимой», если имеются данные, появление которых было бы маловероятно, если предположить, что эта разница отсутствует; это выражение не означает, что данная разница должна быть велика, важна, или значима в общем смысле этого слова.
Уровень значимости обыкновенно обозначают греческой буквой б (альфа). Популярными уровнями значимости являются 5%, 1%, и 0.1%. Если тест выдаёт p-величину меньше б-уровня, то нуль-гипотеза отклоняется. Такие результаты неформально называют «статистически значимыми». Например, если кто-то говорит что «шансы того, что случившееся является совпадением, равны одному из тысячи», то имеется в виду 0.1 % уровень значимости.
19. Сравнение двух средних малых независимых выборок (цель, сущность).
t-критерий является наиболее часто используемым методом, позволяющим выявить различие между средними двух выборок. Еще раз напомним, переменные должны быть измерены в достаточно богатой шкале, например, количественной.
Конечно, применение t-критерия имеет некоторые ограничения, впрочем, очень слабые.
Теоретически t-критерий может применяться, даже если размер выборки очень небольшой (например, 10; некоторые исследователи утверждают, что можно исследовать и меньшие выборки) и если переменные нормально распределены (внутри групп), а дисперсии наблюдений в группах не слишком различны. Известно, что t-критерий устойчив к отклонениям от нормальности.
Предположение о нормальности можно проверить, исследуя распределение (например, визуально с помощью гистограмм) или применяя критерий нормальности. Следует заметить, что эффективно проверить гипотезу о нормальности можно для достаточно большого объема данных (см. замечание Фишера о проверке нормальности, цитированное нами в главе Элементарные понятия анализа данных).
Пусть M 1, M 2 — средние арифметические, σ1,σ2 — стандартные отклонения, а N 1, N 2 — размеры выборок.
В случае с незначительно отличающимся размером выборки применяется упрощённая формула приближенных расчётов:

В случае, если размер выборки отличается значительно, применяется более сложная и точная формула:
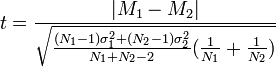
Количество степеней свободы рассчитывается как

20. Сравнение двух средних малых попарно зависимых выборок (цель, сущность).
Для вычисления эмпирического значения t-критерия в ситуации проверки гипотезы о различиях между двумя зависимыми выборками (например, двумя пробами одного и того же теста с временным интервалом) применяется следующая формула:

где Md — средняя разность значений, σ d — стандартное отклонение разностей, а N — количество наблюдений
Количество степеней свободы рассчитывается как

21. Доверительный интервал для оценки генерального среднего нормального распределения. Критерий Стьюдента.
t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.
Если исходная генеральная совокупность н