Для оценки пригодности СИ к измерениям в известном диапазоне с известной точностью вводят метрологические характеристики (далее — MX) СИ с целью:
- обеспечения возможности установления точности измерений;
- достижения взаимозаменяемости СИ, сравнения СИ между собой и выбора нужных СИ по точности и другим характеристикам;
- определения погрешностей измерительных систем и установок на основе MX входящих в их СИ;
- оценки технического состояния СИ при поверке.
По ГОСТ 8.009—84 устанавливают перечень MX, способы их нормирования и формы представления. Каждая из видов MX по назначению может быть представлена более детально с учетом видов самих измерений и СИ в зависимости от изменений влияющих величин или неинформативных параметров входного сигнала.
Неинформативным называется параметр входного сигнала СИ, не связанный функционально с измеряемым параметром. Например, частота переменного тока при измерении его амплитуды.
Нормальные метрологические характеристики (далее — НМХ) устанавливаются документами. MX, определенные документами, считаются действительными. На практике наиболее распространены следующие MX СИ.
Диапазон измерения — область значений измеряемой величины, для которой нормированы допускаемые пределы погрешности СИ (для преобразователей — это диапазон преобразования).
Предел измерения — наибольшее или наименьшее значение диапазона измерения. Для мер — это номинальное значение воспроизводимой величины.
Шкала средств измерения — это упорядоченная совокупность отметок и цифр, соответствующая ряду последовательных значений измеряемой величины.
В шкале Цельсия за начало отсчета принята температура таяния льда, в качестве основного интервала (опорной точки) — температура кипения воды. Одна сотая часть этого интервала — градус Цельсия.
Различают несколько разновидностей шкал:
- шкала наименований — это качественные шкалы, которые не содержат нуля и единиц измерений, здесь присутствуют отношения типа «больше – меньше». Примером может служить шкала цветов (атлас цветов, в графических программах — палитра цветов). Измерение заключается в визуальном сравнении окрашенного предмета с образцами цветов (эталонными образцами атласа цветов). Так как каждый цвет имеет множество оттенков, такое сравнение под силу эксперту, который имеет не только опыт, но и обладает соответствующими особыми характеристиками возможностей визуального наблюдения;
- шкала порядка — свойства величин описывают как отношением эквивалентности, так и отношением порядка по возрастанию или убыванию количественного проявления свойства. В таких шкалах может присутствовать нулевая отметка, но отсутствуют единицы измерения, поскольку невозможно установить, в какое число раз больше или меньше проявляется свойство величины. Обычно шкалы порядка характеризуют значение измеряемой величины (сила ветра, сила землетрясения и т.д.);
- шкала интервалов (разностей). Описывать свойства величин можно не только с помощью отношений эквивалентности и порядка, но и с применением суммирования и пропорциональности интервалов (разностей) между количественными проявлениями данного свойства. Шкалы интервалов имеют условные нулевые значения, а интервалы устанавливаются по согласованию. Такими шкалами являются шкалы времени и длины;
- шкала отношений имеет естественное нулевое значение, а единица измерений устанавливается по согласованию. Например, шкала весов, начинаясь с нулевой отметки, может быть проградуирована по-разному в зависимости от требуемой точности взвешивания;
- абсолютные шкалы всегда имеют определение единицы измерения ФВ;
- условные шкалы — это шкалы ФВ, исходные значения которых выражены в условных единицах, иногда их называют несимметричными. К ним относят шкалы твердости минералов и металлов.
Различают равномерные и неравномерные шкалы. Последние делятся на существенно неравномерные и степенные. Под существенно неравномерной шкалой понимают шкалу с сужающимися делениями, на которой отметка, соответствующая полусумме начального и конечного значения рабочей части шкалы, расположена между 65 и 100 % длины этой рабочей части. Под степенной шкалой понимают шкалу с расширяющимися или сужающимися делениями, но не попадающими под определение существенно неравномерных.
Например, у шкалы на рис.3.6 начальный участок (~20 %) сжат, потому производить отсчеты на нем неудобно. Тогда предел измерения по шкале составляет 50 ед., а диапазон — 10...50 ед.

Рис. 3.6. Неравномерная шкала СИ
Цена деления шкалы — разность значений величин, соответствующих двум соседним отметкам шкалы. Приборы с равномерной шкалой имеют постоянную цену деления, а с неравномерной — переменную. В этом случае нормируется минимальная цена деления.
Чувствительность — отношение изменения сигнала dу на выходе СИ к вызвавшему это изменение изменению dх сигнала на входе:
S = dу/dх. (3.2)
Например, для стрелочного СИ — это отношение перемещения dl конца стрелки к вызвавшему его изменению dx измеряемой величины:
S = dl/dx. (3.3)
Таким образом, для неравномерных шкал величина S = var, и степень неравномерности шкалы оценивают через коэффициент: J = Smax/Smin.
Для равномерных шкал
S = S ср = const и S ср = l / xn, (3.4)
где xn — диапазон измерений.
Чувствительность нельзя отождествлять с порогом чувствительности — наименьшим значением измеряемой величины, вызывающим заметное изменение показаний прибора.
Величину, обратную чувствительности, называют постоянной прибора C =1/ S.
Как правило, выходным сигналом СИ является отсчет (показание) в единицах величины. В этом случае постоянная прибора С равна цене деления. Поэтому для СИ с неравномерной шкалой чувствительность — величина переменная.
Вариация (гистерезис) — разность между показаниями СИ в данной точке диапазона измерения при возрастании и убывании измерений величины и неизменных внешних условиях:
H =| x в – x у | (3.5)
где xв, xу — значения измерений образцовыми СИ при возрастании и убывании величины x. Следует иметь в виду, что, хотя вариация показаний СИ вызывается случайными факторами, сама она — не случайная величина.
Зависимость между выходным и входным сигналом СИ, полученную экспериментально, называют градуировочной характеристикой, которая может быть представлена аналитически, графически или в виде таблицы. Градуировочная характеристика может изменяться под воздействием внешних и внутренних причин. Например, при быстром изучении тока подвижная часть СИ, вследствие инерции, не успевает «следить» за изменением тока. Градуировочная характеристика в этом случае должна выражаться дифференциальным уравнением.
Точность измерения — это степень приближения результатов измерения к некоторому действительному значению физической величины. Чем меньше точность, тем больше погрешность измерения и, соответственно, чем меньше погрешность, тем выше точность.
Класс точности — это обобщенная метрологическая характеристика, определяющая различные свойства средств измерения. Например, у показывающих электроизмерительных приборов класс точности помимо основной погрешности включает вариацию показаний, а у мер электрических величин – величину нестабильности (процентное изменение значение меры в течение года). Класс точности уже включает систематическую и случайную погрешности. Однако он не является непосредственной характеристикой точности измерения, выполняемых с помощью этих СИ, поскольку точность измерения зависит от метода измерения, взаимодействия СИ с объектом, условий измерений и т.д. В частности, для того чтобы измерить величину с точностью до 1%, недостаточно выбрать СИ с погрешностью 1%. Выбранное СИ должно обладать гораздо меньшей погрешностью, так как нужно учесть как минимум еще погрешность метода. Определяя класс точности, нормируют прежде всего пределы допускаемой основной погрешности d осн. В связи с большим разнообразием как самих СИ, так и их МХ, ГОСТ 8.401— 80 устанавливает несколько способов назначения классов точности.
Основная MX СИ — погрешность СИ — есть разность между показаниями СИ и истинными (действительными) значениями ФВ.
Классификация погрешностей СИ:
по отношению к внешним воздействиям:
- основная
- от внешних факторов
- от внутренних факторов
- дополнительная
- случайная
- нестабильность режима работы объекта
- электромагнитные наводки
- неинформативные параметры процесса
- изменение свойств линии связи измерительных калибров
- сбои
- колебание параметров источников питания
- прогрессирующая
- от температуры
- от влаги
- от давления
- от вибрации и ударов
по способу выявления:
- случайная
- систематическая
- методическая
- косвенного измерения
- передачи размера
- квантования по уровню и времени
- вычисления
- алгоритма контрольных операций
- инструментальная
- воздействия СИ на объект
- конечной разрешающей способности
- нормированная погрешность СИ
- постоянная
- периодическая
по характеру режима измерения:
- статическая
- динамическая
- периодических процессов (амплитудная, фазовая, частотная)
- переходных процессов
по способу нормирования МХ:
- абсолютная
- относительная
- приведенная
по взаимодействию с выходным сигналом:
- мультипликативная
- аддитивная.
Все погрешности СИ в зависимости от внешних условий делятся на основные и дополнительные.
Основная погрешность — это погрешность СИ при нормальных условиях эксплуатации. Как правило, нормальными условиями эксплуатации являются: температура 293 ± 5 К или 20 ± 5 °С, относительная влажность воздуха 65 ± 15 % при 20 °С, напряжение в сети питания 220 В ±10 % с частотой 50 Гц ±1 %, атмосферное давление от 97,4 до 104 кПа, отсутствие электрических и магнитных полей (наводок).
В рабочих условиях, зачастую отличающихся от нормальных более широким диапазоном влияющих величин, при необходимости нормируется дополнительная погрешность СИ.
Существуют три способа нормирования основной погрешности СИ:
- нормирование пределов допускаемой абсолютной (±D) или приведенной (± у) погрешностей, постоянных во всем диапазоне измерения;
- нормирование пределов допускаемой абсолютной (±D) или относительной (±s) погрешностей в функции измеряемой величины;
- нормирование постоянных пределов допускаемой основной погрешности, различных для всего диапазона измерений одного или нескольких участков.
В качестве предела допускаемой погрешности выступает наибольшая погрешность, вызываемая изменением влияющей величины, при которой СИ по техническим требованиям может быть допущено к применению. То же самое относится и к дополнительным погрешностям. При этом исходят из следующих положений:
- дополнительная погрешность имеет такой же вид, что и основная (абсолютная, относительная и приведенная);
- дополнительные погрешности, вызванные различными влияющими факторами, должны нормироваться раздельно.
Иногда дополнительную погрешность нормируют в виде коэффициента, указывающего, «на сколько» или «во сколько» изменяется погрешность при отклонении номинального значения. Например, указание, что температурная погрешность вольтметра составляет ±1% на 10 °С, означает, что при изменении среды на каждые 10 °С добавляется дополнительная погрешность 1 %.
Вследствие сложности разделения дополнительных и основных погрешностей поверку СИ выполняют только при нормальных условиях (т. е. дополнительные погрешности исключены).
Случайной погрешностью СИ называют составляющую, изменяющуюся при повторных измерениях одной и той же величины случайным образом (например, вызванные неправильным функционированием механических или электрических элементов измерительного устройства).
Систематическая погрешность СИ — это составляющая общей погрешности, которая остается постоянной или закономерно изменяется при многократных измерениях одной и той же величины (например, если тензосопротивление (изменяется сопротивление от приложенного давления)* плохо наклеено на упругий элемент, то деформация его решетки не будет соответствовать деформации упругого элемента и датчик будет постоянно неправильно реагировать). Различают следующие составляющие систематической погрешности:
- методическая — обусловлена несовершенством метода измерения, приемами использования средств измерения, некорректностью расчетных формул и округления результатов,
- инструментальная — возникает из-за собственной погрешности средств измерения, определяемой классом точности, влиянием средств измерения на результат и ограниченной разрешающей способности средств измерения,
- постоянная
- периодическая.
Выделяют также грубые погрешности которые, как правило, допускаются самим исполнителем, который из-за неопытности или усталости неправильно считывает показания приборов или ошибается при обработке информации. Их причиной могут стать и неисправность средств измерения, и резкое изменение условий измерения.
Статистические погрешности возникают при измерении постоянных величин после завершения переходных процессов в элементах СИ.
Динамическая погрешность — разница между погрешностями СИ в динамическом режиме и его статистической погрешностью.
В соответствии с ГОСТ 8.401—80 для пределов допускаемой основной (и дополнительной) погрешностей предусмотрены различные способы выражения в виде абсолютной, относительной и приведенной погрешности.
Абсолютная погрешность — разность между показаниями x СИ и действительным значением x д измеряемой величины. Выражается она в единицах измеряемой ФВ и может быть задана:
- одним числом D = ± a — аддитивная погрешность или погрешность нуля (неизменна во всем диапазоне измерения);
- в виде линейной зависимости D = ± (a + bx) — мультипликативная погрешность (изменяется пропорционально);
- в виде функции D = f (x), графика или таблицы — присутствует аддитивная и мультипликативная составляющие (рис. 3.7);
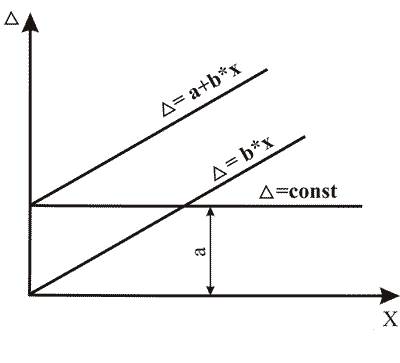
Рис. 3.7. Формирование аддитивной и мультипликативной
составляющих погрешности
Поскольку абсолютная погрешность выражается в абсолютных единицах ФВ, то это не дает возможность сравнивать СИ и измеряющие разные ФВ. Для этой цели можно использовать относительные погрешности D как отношение абсолютной погрешности к действительному x д значению, выраженные в процентах
d = ± (D / x д ) · 100 %. (3.6)
Эта формула показывает, что для одного и того же СИ d уменьшается с ростом x д и приближается к бесконечности (¥) при x д ®0. То есть при измерении на начальном участке шкалы с начальной нулевой отметкой погрешности измерения могут быть сколь угодно велики. Поэтому в метрологии существует принцип запрета измерений на таких участках.
Специфическим видом погрешности цифровых СИ и дискретных преобразователей является погрешность квантования, которая вносится округлением значения измеряемой величины и номинального значения на рис.3.8 приведена текущая разность (погрешность квантования) номинальной (линия 1) и реальной (линия 2) характеристик цифрового СИ в полосе (штриховые линии) погрешностей. Поскольку измеряемая величина x может принимать случайные значения в интервале от от +D до –D, то погрешность квантования есть случайная аддитивная статическая погрешность. Она не зависит ни от текущего значения х, ни от скоростей измерения х во времени. На рисунке 3.8 величина q — шаг квантования по уровню.
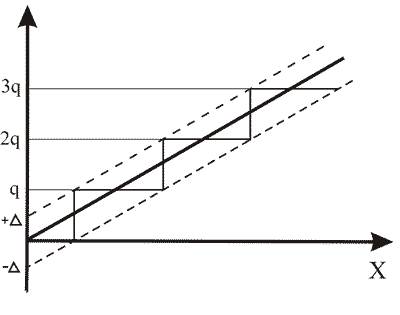
Рис. 3.8. Квантование погрешности цифровых СИ
При многократных измерениях в качестве истинного значения, как правило, используют среднее арифметическое значение.
Калибровка средств измерения
Калибровка средства измерения — совокупность операций, выполняемых с целью определения и подтверждения действительных значений метрологических характеристик и (или) пригодности к применению средства измерения, не подлежащего государственному метрологическому контролю и надзору (далее — ГМНиК).
Из определения можно сделать два вывода:
- калибровка проводится для тех СИ, которые не используются в сферах ГМКиН (установленных ст. 13 Закона РФ от 27.04.93 № 4871—1 «Об обеспечении единства измерений»), а значит, не подлежат поверке;
- калибровка выполняет две функции:
- определение и подтверждение действительных значений метрологических характеристик СИ;
- определение и подтверждение пригодности СИ к применению.
В первом случае лаборатория, калибрующая по заявке (договору) заказчика СИ, не делает вывода о пригодности прибора. Установленные характеристики могут отличаться от паспортных, и только в компетенции заказчика определять, в каких условиях и для каких целей можно и нужно использовать данные СИ.
Во втором случае СИ признается пригодным, если действительное значение его метрологических характеристик соответствует техническим требованиям, установленным в НД или заказчиком. Вывод о пригодности СИ в этом случае делает калибровочная лаборатория.
В решаемых на практике измерительных задачах калибровка может сводиться только к проверке пригодности СИ, т.е. его работоспособности. В частности, требуется знать не действительные значения измеряемой величины, нужно лишь констатировать наличие величины измеряемого сигнала определенного уровня. Примером может служить калибровка устройств — сигнализаторов предельного значения температуры. В сигнализаторах, имеющих одну или несколько сигнальных лампочек, включение или выключение последних свидетельствует о достижении предельных значений величины. В устройствах, имеющих шкалу в виде нескольких цветовых секторов (подобных посуде фирмы «Цептер»), положение указательной стрелки в пределах конкретного сектора означает определенное состояние объекта измерений.
Калибровка может быть возложена как на МС юридического лица, так и на любую другую организацию, способную выполнить калибровочные работы.
Результаты калибровки СИ удостоверяются калибровочным знаком, наносимым на СИ, записью в эксплуатационных документах или сертификатом о калибровке.
На основе договоров, заключаемых с государственными научными метрологическими центрами или органами ГМС, заинтересованные МС юридических лиц могут быть аккредитованы на право проведения калибровочных работ. В этих случаях последним предоставляется право выдавать сертификаты о калибровке от имени органов и организаций, которые их аккредитовали.
Аккредитация — процедура добровольная. В каких случаях она необходима? Прежде всего, тогда, когда предприятие поставляет продукцию на зарубежные рынки. В этом случае торговый партнер (покупатель) может потребовать от продавца подтверждения того, что характеристики продукции измерялись приборами, проверенными аккредитованной МС.
В 1994—1995 гг. в России сформировалась Российская система калибровки (РСК). В «Положении о Российской системе калибровки» регламентированы следующие вопросы:
- организация, структура и функции РСК;
- права и обязанности входящих в нее юридических лиц независимо от форм собственности и пр.
В создании РСК соблюден ряд принципов:
- Во-первых, система создается на добровольной основе. Никто не вправе навязывать аккредитацию МС. Добровольность вступления в РСК предусматривает процедуру признания, а следовательно, и выполнения всех действующих в системе НД.
- Во-вторых, в качестве аккредитующих органов могут выступать государственные научные метрологические центры и органы ГМС.
- В-третьих, аккредитованная МС выдает сертификаты и ставит оттиски калибровочных клейм от имени аккредитующего органа.
- В-четвертых, РСК строится на принципе компетентности, в соответствии с которым аккредитацию МС проводят аккредитующие органы, компетентные в заявленной области аккредитации.
- В-пятых, это принцип самоокупаемости. Он означает, что аккредитация МС является платной услугой.