Пусть задана СЛАУ, в которой число уравнений равно числу неизвестных:
 (2)
(2)
Рассмотрим матрицу А из коэффициентов при неизвестных (матрицу системы), матрицу-столбец X из неизвестных величин и матрицу-столбец, составленную из свободных членов системы:
 ,
,  ,
,  .
.
Тогда левую часть системы (2) можно записать в виде произведения матриц A·X, а правую – в виде матрицы B. Следовательно, исходная система запишется в эквивалентной ей матричной форме:
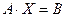 (3)
(3)
Равнозначность записей (2) и (3) легко проверяется с помощью операции умножения матриц (проверьте!).
Таким образом, решить СЛАУ (2) значит найти матрицу X, удовлетворяющую уравнению (3).
Если определитель матрицы системы det A ≠ 0, то матрица A имеет обратную матрицу  .
.
Обратной для матрицы А называется такая матрица  , которая удовлетворяет условию:
, которая удовлетворяет условию:
 ,
,
где Е – единичная матрица, т.е. матрица, на главной диагонали которой стоят единицы, а все остальные элементы равны нулю).
Умножим обе части матричного уравнения (3) слева на матрицу  , получим:
, получим:
 .
.
Так как  , а по свойству единичной матрицы
, а по свойству единичной матрицы  , то
, то
 (4)
(4)
Нетрудно проверить, что матрица X, определяемая формулой (4), является решением уравнения (3), и это решение единственно.
Формулу (4) называют матричной записью решения системы линейных уравнений. Чтобы воспользоваться формулой (4), необходимо сначала найти обратную матрицу  .
.
Рассмотрим
АЛГОРИТМ НАХОЖДЕНИЯ ОБРАТНОЙ МАТРИЦЫ
Первый шаг. Вычислить определитель матрицы системы.
Если det A≠0, то  существует.
существует.
Второй шаг. Построить матрицу  , состоящую из алгебраических дополнений соответствующих элементов матрицы A:
, состоящую из алгебраических дополнений соответствующих элементов матрицы A:
 ,
,
где  ,
,
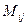 – минор элемента
– минор элемента  , для всех i, j =1, 2, …, n.
, для всех i, j =1, 2, …, n.
Третий шаг. Транспонировать матрицу  , то есть построить присоединенную матрицу
, то есть построить присоединенную матрицу 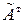 :
:

Четвертый шаг. Разделить каждый элемент присоединенной матрицы 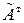 на величину определителя det A.
на величину определителя det A.
Таким образом, получена обратная матрица по формуле:
 .
.
Для отыскания решения СЛАУ (1) теперь необходимо вернуться к уравнению (4) и перемножить найденную матрицу  и матрицу-столбец B.
и матрицу-столбец B.
Пример 2.1. Решить матричным способом систему линейных уравнений:
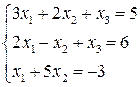
Решение. Найдем предварительно обратную матрицу системы  .
.
1. 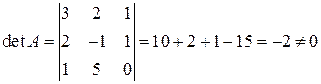 , следовательно,
, следовательно,  существует.
существует.
2. Найдем алгебраические дополнения элементов матрицы А:
 ;
;  ;
;  ;
;
 ;
;  ;
; 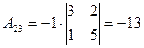 ;
;
 ;
;  ;
;  .
.
Строим матрицу,  , состоящую из алгебраических дополнений:
, состоящую из алгебраических дополнений:
 .
.
3. Транспонированием матрицы  получаем присоединенную матрицу:
получаем присоединенную матрицу:
 .
.
4. Определяем матрицу  :
:
 =
=  .
.
Решение системы находим по формуле (4):
 =
= 

 .
.
Ответ: 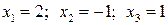 .
.
Пример 2.2. Решить матричным способом систему линейных уравнений:
 .
.
Решение будем искать, в соответствии с формулой (3), в виде:
 .
.
Запишем матрицы:
 ,
,
где А – матрица коэффициентов при неизвестных;
Х – матрица-столбец неизвестных х1, х2, х3;
B – матрица-столбец из свободных членов.
1°. Определитель матрицы А
 ,
,
следовательно, обратная матрица для матрицы А существует. Построим ее.
2°. Найдем алгебраические дополнения элементов матрицы А:
 ;
;  ;
;  ;
;
 ;
;  ;
; 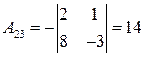 ;
;
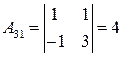 ;
;  ;
;  .
.
Запишем матрицу  , состоящую из алгебраических дополнений:
, состоящую из алгебраических дополнений:
 .
.
3°. Транспонируем матрицу  и получаем присоединенную матрицу:
и получаем присоединенную матрицу:
 .
.
4°. Строим обратную матрицу:  =
=  .
.
Подставив в уравнение (3) соответствующие матрицы, имеем
 ,
,
откуда х 1=2, х 2=4, х 3= – 1.
Проверка.
 Все уравнения системы обратились в тождества.
Все уравнения системы обратились в тождества.
Ответ:  .
.
Пример 2.3. Решить систему линейных алгебраических уравнений методом обратной матрицы

Решение.
1°. Запишем определитель матрицы A и вычислим его:
 .
.
Так как определитель не равен нулю, то матрица А имеет обратную. Найдем обратную матрицу.
2°. Найдем алгебраические дополнения элементов матрицы А:
 ;
;  ;
;  ;
;
 ;
;  ;
; 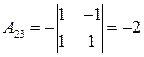 ;
;
 ;
;  ;
; 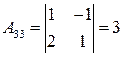 .
.
Составим матрицу  из алгебраических дополнений:
из алгебраических дополнений:
 .
.
3°. Транспонируем матрицу  и получим присоединенную матрицу:
и получим присоединенную матрицу:
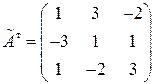 .
.
4°. Строим обратную матрицу:  =
= 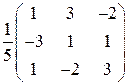 .
.
Найдем решение системы:

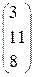 =
= 
 =
=  .
.
Таким образом, решением системы является тройка чисел: х 1=4, х 2=2, х 3=1.
Проверка.
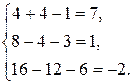 Все уравнения системы обратились в тождества.
Все уравнения системы обратились в тождества.
Ответ: х 1=4, х 2=2, х 3=1.
Примеры для самостоятельного решения (под контролем преподавателя).
Решить системы линейных алгебраических уравнений матричным способом:
Пример 2.4. 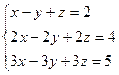 .
.
Решение.
1°. Определитель матрицы системы:
 ,
,
следовательно, обратной матрицы не существует.
Проанализируем систему уравнений. Умножим второе уравнение на  и вычтем его из третьего. Получим:
и вычтем его из третьего. Получим:  , что невозможно, то есть второе и третье уравнения противоречивы.
, что невозможно, то есть второе и третье уравнения противоречивы.
Ответ: система несовместна.
Пример 2.5. 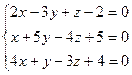 .
.
Решение.
1°. Определитель матрицы A:
 .
.
Определитель не равен нулю, матрица А имеет обратную.
2°. Алгебраические дополнения элементов матрицы А:
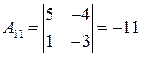 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
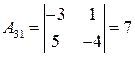 ;
;  ;
;  .
.
Составим матрицу  алгебраических дополнений:
алгебраических дополнений:
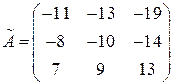 .
.
3°. Запишем присоединенную матрицу:
 .
.
4°. Обратная матрица:  =
=  .
.
Решение системы:
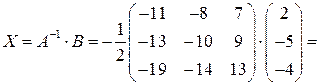
 .
.
Проверка
 .Все уравнения системы обратились в тождества.
.Все уравнения системы обратились в тождества.
Ответ:  .
.
Задание на самоподготовку:
1. Решить системы линейных уравнений с помощью определителей:
а)  ; б)
; б) 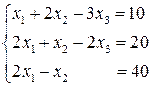 ; в)
; в) 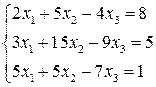 .
.
Ответы:
а)  ;
;
б)  ;
;
в) Решений нет (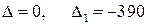 ).
).
2. Решить системы линейных уравнений матричным способом:
а)  б)
б) 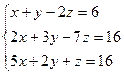
Ответы: а)  ; б)
; б) 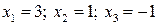 .
.