Рассмотрим на координатной плоскости окружность радиуса 1 с центром в начале координат. Ее называют единичной окружностью. Введем понятие поворота точки единичной окружности во круг начала координат на угол α радиан, где α – любое действительное число.
1. 1. Пусть α>0. Предположим, что точка, двигаясь поединичной окружности от точки Р против часовой стрелки, прошла путь длиной α (рис. 1). Конечную точку пути обозначим М.
В этом случае будем говорить, что точка М получена из точки Р поворотом вокруг начала координат на угол α радиан.
2. 2. Пусть α<0. В этом случае поворот на угол α радиан означает, что движение совершалось по часовой стрелке и точка прошла путь длинной (рис. 2).
Поворот на 0 рад означает, что точка остается на месте.
15. Вопрос: Определение синуса, косинуса, тангенса и котангенса угла. Основное тригонометрическое тождество.
Ответ:
Синус угла - это отношение противолежащего катета к гипотенузе;
Косинус угла - это отношение прилежащего катета к гипотенузе;
Тангенс угла - это отношение противолежащего катета к прилежащему;
Котангенс угла – этоотношение прилежащего катета к противолежащему.
Основное тригонометрическое тождество:

16. Вопрос: Формулысложенияcos(a±b), sin(a±b),tg(a±b),cosa±cosb, sina±sinb
Ответ:

17. Вопрос: Формулы синуса, косинуса, тангенса двойного и половинного угла.
Ответ:
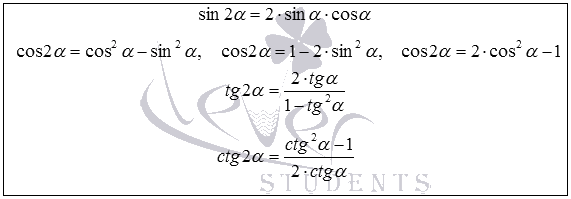

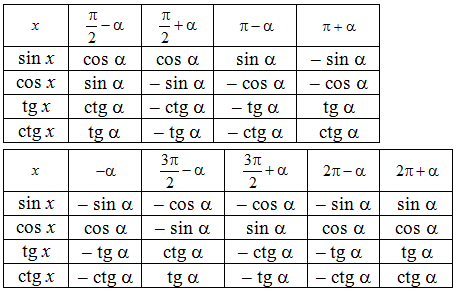
18. Вопрос: Формулы приведения, вывод, примеры.
Ответ:

19. Вопрос: Уравнения вида cosx = a, sinx = a, tgx = a. Общие виды решений и частные случаи.
Ответ:
Решение уравнения sin x = a
| Обычная форма записи решения | 
|
| Более удобная форма записи решения | 
|
| Ограничения на число a | В случае, когда  , уравнение решений не имеет , уравнение решений не имеет
|
Графическое обоснование решения уравнения sin x = a представлено на рисунке 1

Рис. 1
Частные случаи решения уравнений sin x = a
| Уравнение | Решение |
| sin x = – 1 | 
|

| 
|
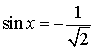
| 
|

| 
|
| sin x = 0 | 
|

| 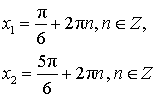
|

| 
|

| 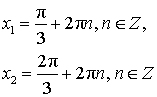
|
| sin x = 1 | 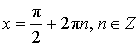
|
Решение уравнения cos x = a
| Обычная форма записи решения | 
|
| Более удобная форма записи решения | 
|
| Ограничения на число a | В случае, когда  , уравнение решений не имеет , уравнение решений не имеет
|
Графическое обоснование решения уравнения cos x = a представлено на рисунке 2
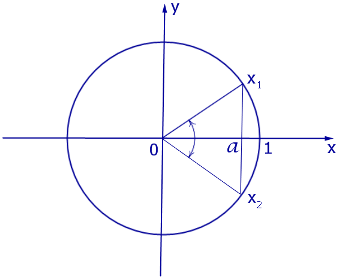
Рис. 2
Частные случаи решения уравнений cos x = a
| Уравнение | Решение |
| cos x = – 1 | 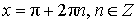
|

| 
|

| 
|
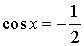
| 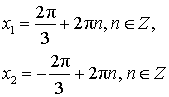
|
| cos x = 0 | 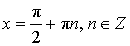
|
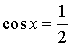
| 
|
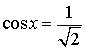
| 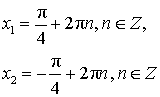
|

| 
|
| cos x = 1 | 
|
Решение уравнения tg x = a
| Обычная форма записи решения | 
|
| Более удобная форма записи решения | 
|
| Ограничения на число a | Ограничений нет |
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3

Рис. 3
Частные случаи решения уравнений tg x = a
| Уравнение | Решение |

| 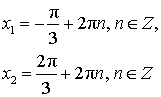
|
| tg x = – 1 | 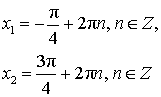
|

| 
|
| tg x = 0 | 
|

| 
|
| tg x = 1 | 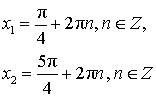
|
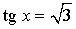
| 
|
20(1). Вопрос: Определение производной, правила дифференцирования, примеры.
Ответ: Производная функции − одно из основных понятий математики, а в математическом анализе производная наряду с интегралом занимает центральное место. Процесс нахождения производной называется дифференцированием. Обратная операция − восстановление функции по известной производной − называется интегрированием.
Производная функции в некоторой точке характеризует скорость изменения функции в этой точке.
f′(x)=y′(x)=df/dx=dy/dx

Геометрия
1. Вопрос: Аксиомы стереометрии. Следствия из аксиом (доказать одно из них).
Ответ: А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
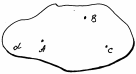
| А   В В   (точки А, В, С лежат в плоскости (точки А, В, С лежат в плоскости  ) С ) С  
|
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
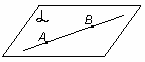
| АB   Прямая АВ лежит в плоскости Прямая АВ лежит в плоскости 
|
Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.

| а   = М Прямая а и плоскость = М Прямая а и плоскость  пересекаются в точке М. пересекаются в точке М.
|
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

|    = a = a  и и  пересекаются по прямой а. пересекаются по прямой а.
|
Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Доказательство:
1) Рассмотрим прямую a и точку A, которая не находится на этой прямой.
2) На прямой a выберем точки B и C.
3) Так как все 3 точки не находятся на одной прямой, из второй аксиомы следует, что через точки A, B, C и можно провести одну единственную плоскостьα.
4) Точки прямой a, B и C, лежат на плоскости α, поэтому из третьей аксиомы следует, что плоскость проходит через прямую a и, конечно, через точку A.
Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
2. Вопрос: Теорема о параллельности трех прямых (формулировка и доказательство).
Ответ: Две прямые, параллельные третьей прямой, параллельны.
Дано: a ∥ c и b ∥ c
Доказать: a ∥ b
Доказательство:
Выберем точку M на прямой b.
Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
Пусть прямая b пересекает плоскость α.
Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a ∥ c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным.
Значит, прямая b находится в плоскости α.
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L.
Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по теореме (Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и при том только одну.) это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
3. Вопрос: Параллельные прямые в пространстве(определение). Теорема о параллельных прямых.
Ответ: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Теорема о параллельных прямых: Через любую точку пространства, не лежащую на данной прямой проходит прямая, параллельная данной, и притом только одна.
4. Вопрос: Параллельность прямой и плоскости(определение). Признак параллельности прямой и плоскости.
Ответ: Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости: Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то прямая параллельна самой плоскости.
5. Вопрос: Расположение прямых в пространстве(виды). Признак скрещивающихся прямых.
Ответ: 
Признак скрещивающихся прямых: Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.
6. Вопрос: Углы с сонаправленными сторонами. Определение, теорема.
Ответ:


7. Вопрос: Признак параллельности двух плоскостей.
Ответ: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то плоскости параллельны.
8. Вопрос: Свойства параллельности плоскостей(доказать одно из них)
Ответ: Всего 3 свойства.
С1: Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Доказательство:
Пусть даны параллельные плоскости  и
и  и плоскость
и плоскость  , которая пересекает плоскости
, которая пересекает плоскости  и
и  по прямым а и b соответственно (Рис. 1.).
по прямым а и b соответственно (Рис. 1.).

Рис. 1.
Прямые а и b лежат в одной плоскости, а именно в плоскости γ. Докажем, что прямые а и b не пересекаются.
Если бы прямые а и b пересекались, то есть имели бы общую точку, то эта общая точка принадлежала бы двум плоскостям и  , и
, и  , что невозможно, так как они параллельны по условию.
, что невозможно, так как они параллельны по условию.
Итак, прямые а и b параллельны, что и требовалось доказать.
С2: Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

Рис. 2.
Доказательство:
Пусть даны параллельные плоскости  и
и  и параллельные прямые АВ и СD, которые пересекают эти плоскости (Рис. 2.). Докажем, что отрезки АВ и СD равны.
и параллельные прямые АВ и СD, которые пересекают эти плоскости (Рис. 2.). Докажем, что отрезки АВ и СD равны.
Две параллельные прямые АВ и СD образуют единственную плоскость γ, γ = АВDС. Плоскость γ пересекает параллельные плоскости  и
и  по параллельным прямым (по первому свойству). Значит, прямые АС и ВD параллельны.
по параллельным прямым (по первому свойству). Значит, прямые АС и ВD параллельны.
Прямые АВ и СD также параллельны (по условию). Значит, четырехугольник АВDС – параллелограмм, так как его противоположные стороны попарно параллельны.
Из свойств параллелограмма следует, что отрезки АВ и СD равны, что и требовалось доказать.
С3: Параллельные плоскости рассекают стороны угла на пропорциональные части.
Доказательство:
Пусть нам даны параллельные плоскости  и
и  , которые рассекают стороны угла А (Рис. 3.). Нужно доказать, что
, которые рассекают стороны угла А (Рис. 3.). Нужно доказать, что 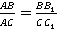 .
.
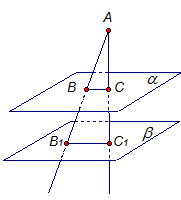
Рис. 3.
Параллельные плоскости  и
и  рассечены плоскостью угла А. Назовем линию пересечения плоскости угла А и плоскости
рассечены плоскостью угла А. Назовем линию пересечения плоскости угла А и плоскости  – ВС, а линию пересечения плоскости угла А и плоскости
– ВС, а линию пересечения плоскости угла А и плоскости  – В1С1. По первому свойству, линии пересечения ВС и В1С1 параллельны.
– В1С1. По первому свойству, линии пересечения ВС и В1С1 параллельны.
Значит, треугольники АВС и АВ1С1 подобны. Получаем:
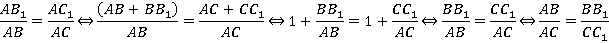 .
.
9. Вопрос: Тетраэдр и параллелепипед. Определения. Свойства параллелепипеда.
Ответ: Тетраэдр - поверхность, составленная из четырёх треугольников DАВ, DВС, DАС и АВС.

| 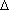 АВС, АВС,  DАС, DАС,  DВС, DВС,  DАВ - грани. отрезки DА, DВ, АВ и т.д. - рёбра. точки А, В, С и т.д. - вершины. Рёбра АD и ВС - противоположные. Считается DАВ - грани. отрезки DА, DВ, АВ и т.д. - рёбра. точки А, В, С и т.д. - вершины. Рёбра АD и ВС - противоположные. Считается  АВС - основание, остальные грани - боковые. АВС - основание, остальные грани - боковые.
|
Параллелепипед. АВСDA1B1C1D1: поверхность, составленная из двух равных параллелограммов АВСD и A1B1C1D1, лежащих в параллельных плоскостях и четырёх параллелограммов.
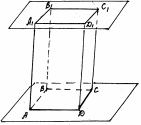
| все параллелограммы - грани, их стороны - рёбра, их вершины - вершины параллелепипеда. Считается: АВСD и A1B1C1D1 - основания, остальные грани - боковые. |
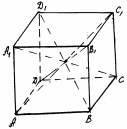 рис. 29 рис. 29
| Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда: A1C, D1B, AC1, DB1. |
Свойства:
1. Противоположные грани параллелепипеда параллельны и равны.
Доказательство:
Для любой пары противолежащих граней параллелепипеда имеем: соответствующие углы равны (например,  ,
,  и т. д.); соответствующие стороны равны и параллельны (
и т. д.); соответствующие стороны равны и параллельны ( и
и  ,
,  и
и  и т. д. как противолежащие стороны параллелограммов). Отсюда
и т. д. как противолежащие стороны параллелограммов). Отсюда 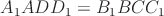 и их плоскости параллельны.
и их плоскости параллельны.
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
10. Вопрос: Признак перпендикулярности прямой и плоскости.
Ответ:Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
11. Вопрос: Теорема о трёх перпендикулярах.
Ответ: Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

12. Вопрос: Признак перпендикулярности двух плоскостей.
Ответ: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
13. Вопрос: Призма. Основные элементы, Sбок, Sполн, Vпризмы.
Ответ: Призма — это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани — параллелограммами.
Sбок=Pосн*h,
Sполн= 2Sосн+Sбок,
Vпризмы =Sосн*h.
14. Вопрос: Пирамида. Основные элементы, Sбок, Sполн, Vпирамиды.
Ответ: Пирамида – многогранник, одна из граней которого (называется основанием) – произвольный многоугольник, а остальные грани соединяются в одной точке(вершине).
Sбок=Pосн*l
Sполн = Sбок +Sосн
Vпирамиды = (1/3)*Sосн*h
15. Вопрос: Усечённаяпирамида. Основные элементы, Sбок, Sполн.
Ответ: Усечённой пирамидой называется часть пирамиды, заключенная между её основанием и сечением пирамиды, параллельным основанию.
Sбок. ус. = (1/2)(P1осн+P2осн)l, l–апофема.
Sполн=Sбок. ус.+S1осн+S2осн.
16. Вопрос: Двугранный угол. Градусная мера двугранного угла.
Ответ: Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой.Двугранный угол измеряется величиной своего линейного угла.Чтобы найти величину двугранного угла или угла между плоскостями, нужно построить линейный угол и найти величину этого линейного угла.
17. Вопрос: Прямоугольный параллелепипед. Свойства прямоугольного параллелепипеда (доказать одно из них).
Ответ: Прямоугольный параллелепипед - многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником. Противолежащие грани параллелепипеда равны.
Свойства прямоугольного параллелепипеда:
С1: В прямоугольном параллелепипеде все шесть граней прямоугольники.
АВСD и А1В1С1D1 – прямоугольники по определению.
С2: Боковые ребра перпендикулярны основанию. Значит, все боковые грани прямоугольного параллелепипеда - прямоугольники.
С3: Все двугранные углы прямоугольного параллелепипеда прямые.
Рассмотрим, например, двугранный угол прямоугольного параллелепипеда с ребром АВ, т. е. двугранный угол между плоскостями АВВ1 и АВС.
АВ – ребро, точка А1 лежит в одной плоскости – в плоскости АВВ1, а точка D в другой – в плоскости А1В1С1D1. Тогда рассматриваемый двугранный угол можно еще обозначить следующим образом: ∠А1АВD.
Возьмем точку А на ребре АВ. АА1 – перпендикуляр к ребру АВ в плоскости АВВ1, AD перпендикуляр к ребру АВ в плоскости АВС. Значит, ∠А1АD –линейныйуголданногодвугранногоугла. ∠А1АD = 90°, значит, двугранныйуголприребреАВравен 90°.
∠(АВВ1, АВС) = ∠(АВ) = ∠А1АВD= ∠А1АD = 90°.
Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые.
18. Вопрос: Понятие многогранника. Виды. Примеры.
Ответ: Если поверхности геометрических тел составлены из многоугольников, то такие тела называются многогранниками.
Виды:
1. Пирамида
· Усечённая пирамида
2. Призма
3. Параллелепипед
· Куб
· Прямоугольный параллелепипед
4. Конус
· Усеченный конус
19. Вопрос: Правильная пирамида. Определение, Sбок.
Ответ: Пирамида называется правильной, если её основанием является правильный многоугольник, при этом вершина такой пирамиды проецируется в центр ее основания.
Sбок=Pосн*l, l – апофема.
20. Вопрос: Симметрия в пространстве. Правильные многогранники.
Ответ: Точки А и A1 называются симметричными относительно точки О (центра симметрии), если О – середина отрезка AA1. Точка О симметрична сама себе.
Точки А и A1 называются симметричными относительно прямой а (ось симметрии) если прямая а проходит через середину отрезка AA1 и перпендикулярна ему. Каждая точка прямой a симметрична сама себе.
Точки А и A1 называются симметричными относительно плоскости a (плоскость симметрии) если плоскость a проходит через середину отрезка AA1 и перпендикулярна ему. Каждая точка плоскости a симметрична сама себе.
Правильные многоугольники:
· Куб
· Правильный тетраэдр
· Правильная пирамида
· Правильный октаэдр
· Правильный икосаэдр
· Правильный додекаэдр
21. Вопрос: Уравнение сферы. Взаимное расположение сферы и плоскости.
Ответ: Уравнение сферы: (x-x0)2+(y-y0)2+(z-z0)2=R2
Взаимное расположение сферы и плоскости:
1. Плоскость не пересекает сферу;
2. Плоскость касается сферы;
3. Плоскость пересекает сферу.

22. Вопрос: Касательная плоскость к сфере. Свойство с доказательством.
Ответ: Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Свойство: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
Доказательство: Из условия свойства следует, что данный радиус является перпендикуляром, проведенным из центра сферы к данной плоскости. Поэтому расстояние от центра сферы до плоскости равно радиусу сферы, и, следовательно, сфера и плоскость имеют только одну общую точку. Это и означает, что данная плоскость является касательной к сфере.
23. Вопрос: Цилиндр. Основные элементы, Sбок, Sполн, Vцилиндра.
Ответ: Цилиндр – тело, которое состоит из двух кругов, лежащих в параллельных плоскостях и всех отрезков, соединяющих соответствующие линии этих кругов.
Sбок=2πrh, r– радиус, h– высота;
Sполн= Sбок+ 2Sосн=2πrh+2πr2=2πr(h+r)
Vцилиндра= Sосн*h=πr2h
24. Вопрос: Конус. Основные элементы, Sбок, Sполн, Vконуса.
Ответ: Конусом называется тело, которое состоит из круга, точки и всех отрезков, соединяющих эту точку с точкой круга. Круг называется основанием, а отрезки - образующими. Точка называется вершиной, а высота конуса перпендикуляр, проведённый из вершины конуса к основанию.
Sбок= πrl;
Sполн= Sбок+ Sосн= πrl + πr2 = πr(l+r)
Vконуса = (1/3)*πr2h
25. Вопрос:Шар и сфера, основные элементы, Sсферы, Vшара.
Ответ: Сфера – геометрическое место точек в пространстве, равноудалённых от некоторой заданной точки (центра сферы). Расстояние между любой точкой сферы и её центром называется радиусом. Геометрическое тело, ограниченное сферой, называется шаром.
Sсферы = 4*πR2
Vшара = (4/3)* πR3