11.2.1 Телефонной нагрузкой (ТН) называется случайная величина, которая определяется числом вызовов, поступающих на коммутатор телефонной станции от абонентов телефонной сети в единицу времени с учетом времени обслуживания каждого вызова. Время 
обслуживания 
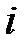-го вызова включает интервалы времени установления соединения абонентов, предоставления им канала связи на время переговоров и разъединения.
Важнейшей характеристикой ТН является её интенсивность (часо-занятие), которая равна произведению математического ожидания числа вызовов, поступающих в единицу времени, 
на среднее время 
обслуживания одного вызова, отнесенная к интервалу времени 1 час, т.е. 
.
Единицей измерения интенсивности ТН служит эрланг (1 Эрл), который равен ТН в одно часо-занятие канала за промежуток времени равный одному часу. Следовательно, если ТН превышает 1Эрл, то в канале возникают очереди на обслуживание или отказы в обслуживании, если организация очередей не предусмотрена.
Одним из первопроходцев анализа телекоммуникационного трафика был датчанин Агнер К. Эрланг (1878 ÷ 1929). На примере небольшой деревни он оценил ту часть абонентов местной телефонной станции, которая пыталась установить соединение с абонентами за пределами деревни. В 1909 году он опубликовал работу «Теория вероятностей и телефонные соединения», в которой были приведены формулы расчета параметров телефонного трафика, принятые Английским Почтамтом. Единица измерения телекоммуникационного трафика была названа в его честь «Эрланг».
Поскольку ТН – величина случайная и не стационарная, то разработчиков и специалистов по обслуживанию сетей интересует структура вызовов в часы наибольшей нагрузки, когда сеть максимально нагружена. Оценка телекоммуникационного трафика в Эрлангах позволяет вычислить количество необходимых каналов в конкретной зоне обслуживания абонентов района, области, базовой станции и т.п.
|
|
Телефонная нагрузка подвержена значительным колебаниям по месяцам года, дням недели и особенно по часам суток. Непрерывный интервал времени длительностью 60 мин в пределах суток, в течение которого наблюдается, в среднем, наибольшая величина ТН, называется часом наибольшей нагрузки (ЧНН). Обычно ТН в ЧНН в 2÷5 раз превышает среднесуточную ТН, её доля от суммарной суточной нагрузки достигает в крупных городах 0,1.
Статистические исследования характера ТН, проводимые среди одинаковых абонентских групп, позволяют выявить вероятностные распределения ТН и ЧНН по величине, времени суток, каналам связи и т.д. По этим данным аналитически выводится, так называемое, расчётное значение (
) интенсивности ТН, используемое при установлении масштаба телефонных сетей, необходимого для обеспечения требуемого качества обслуживания абонентов: количества единиц оборудования телефонных станций; количества и распределения каналов связи, объема кабельной системы, объема сооружений и пр.
В телефонной сети с полнодоступными неблокируемыми абонентскими линиями вероятность потерь при обслуживании абонентов (вероятность получения коротких гудков в ответ на вызов абонента) можно рассчитать по первой формуле Эрланга
,
где 
– расчётное значение интенсивности телефонной нагрузки (в Эрл), поступающей на коммутатор АТС, по любой из v абонентских линий; 
– порядковый номер активной абонентской линии.
|
|
Вероятность того, что все каналы в сети будут свободны (в среднем доля времени в течение суток, когда сеть не загружена) вычисляется по формуле
,
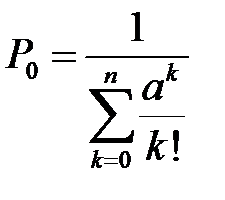где 
.
Для облегчения расчетов первая формула Эрланга табулирована и представлена на рисунке 11.1.
Рисунок 11.1 – Зависимость вероятности отказов от предлагаемой ТН для сетей с числом v абонентских линий
Эта формула рассматривается в первой концепции теории Эрланга – Erlang В, которая относится к телефонным сетям и служит для предсказания вероятности блокирования вызова. Она дает возможность при известной интенсивности ТН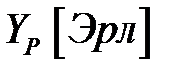 
определить число требуемых каналов связи 
которые обеспечат приемлемую заданную вероятность отказов 
. При этом в модели сети, согласно концепции Erlang В, приняты следующие допущения:
– количество абонентов (пользователей) бесконечно велико;
– интервалы между вызовами случайные;
– длительность вызовов – случайная величина;
– время установления соединения ничтожно мало;
– блокированные вызовы (отказы) не рассматриваются;
– ресурсы предоставляются в соответствие с порядком поступления запроса.
11.2.2 В общем случае закон Эрланга формулируется следующим образом. Пусть имеется n независимых случайных величин xi, каждая из которых имеет экспоненциальное (показательное) распределение с одним и тем же параметром 
(лямбда) 
, 
. Тогда сумма этих случайных величин – величина 
, будет иметь распределение плотности вероятностей значений x по диапазону их возможных значений в виде
|
|
.
Среднее значение и дисперсия случайной величины x равны соответственно 
и 
.
Этот закон получил название «Распределение Эрланга» в честь А. Эрланга (A. Erlang), впервые применившего его в задачах теории массового обслуживания и телефонии. Закон Эрланга широко используется в задачах анализа систем телекоммуникаций для моделирования входящего потока данных или вызовов (нагрузки на сеть) при установлении связи.
11.2.3 Рассмотрим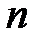 
-канальную систему массового обслуживания с отказами, т.е. с невозможностью обслуживания заявок при сохранении физической работоспособности. Пусть на вход системы поступает простейший поток заявок с плотностью 
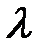заявок в секунду. Время обслуживания заявки является случайной величиной, например, из-за случайного объема заявки на обслуживание (в компьютерной сети – пакета), и имеет экспоненциальное распределение с параметром 
, где 
– среднее время обслуживания заявки (в компьютерной сети – среднее время коммутации пакета).
Сразу после включения системы, режим ее работы будет нестационарным, поскольку начнется «переходный», процесс, как во всякой динамической системе, описываемой дифференциальными уравнениями. Однако по истечении определенного времени, переходный процесс затухнет, и система перейдет на стационарный «установившийся» режим, вероятностные характеристики которого уже не будут зависеть от времени.
На практике большой интерес представляют характеристики систем телекоммуникаций в установившемся режиме обслуживания. В теории массового обслуживания доказано, что для любой системы с отказами установившийся режим существует. Это значит, что при устремлении времени анализа системы к бесконечности все вероятности 
стремятся к своим предельным значениям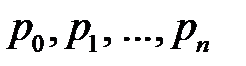 
, а все производные вероятностей – к нулю.
Чтобы найти предельные значения вероятностей состояний системы в установившемся режиме, в дифференциальных уравнениях, описывающих процессы в ней, все вероятности заменяются их предельными значениями, а производные приравниваются нулю. После такой замены анализируется система алгебраических уравнений вида
К этим уравнениям добавляется условие нормировки в виде 
, смысл которого состоит в том, что сумма вероятностей всех n возможных состояний системы должна быть равна единице.
Из системы уравнений, выражая неизвестные вероятности 
через 
и параметры 
и 
, путём последовательной их подстановки получим:
– из первого уравнения 
;
– из второго уравнения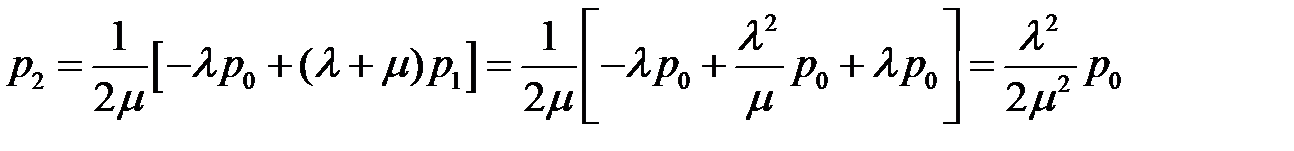 
;
– и т.д.;
– в общем случае 
для любого 
.
Полученные выражения можно преобразовать в более удобную для вычислений форму путём подстановки параметра 
, который именуется приведенной плотностью потока заявок, и определяется как среднее число заявок, приходящееся на среднее время обслуживания одной заявки, поскольку .
В новых обозначениях формулы для расчёта вероятностей состояний системы при известной вероятности состояния 
примут вид
.
Чтобы определить используем очевидное равенство 
, откуда следует, что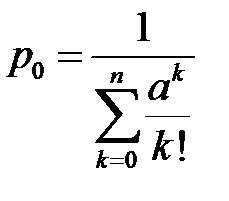 
.
Окончательно, выражение для расчета вероятностей состояний системы, содержащее только параметры 
принимает вид
Полученное выражение называется формулой Эрланга, которая позволяет вычислить вероятность количества k занятых каналов в системе массового обслуживания, содержащей n каналов, в зависимости от характеристик потока заявок и производительности системы.
Полагая k = n, получим формулу вероятности отказа обслуживания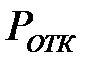 
системой поступающей заявки, т.е. вероятность того, что все каналы окажутся занятыми при поступлении заявки на обслуживание.
.
В частности, для одноканальной системы при n=1 вероятность отказа обслуживания определяется из выражения
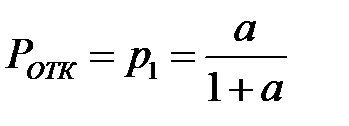, а относительная пропускная способность определится как 
.
Формулы Эрланга и их следствия выведены для случая показательного распределения времени обслуживания. Однако исследования последних лет показали, что эти формулы остаются справедливыми и при любом законе распределения времени обслуживания, лишь бы входной поток был простейшим (пуассоновским).
Несмотря на то, что формулы Эрланга в точности справедливы только при простейшем потоке заявок, ими можно с известным приближением пользоваться и в случае, когда поток заявок отличается от простейшего, например, является стационарным потоком с ограниченным последействием, т.е. зависимостью последующего состояния системы от ограниченного числа предшествовавших состояний. Расчеты показывают, что замена произвольного стационарного потока с не очень большим последействием простейшим потоком той же плотности, как правило, мало влияет на характеристики пропускной способности системы.
Кроме того, можно пользоваться формулами Эрланга в приближенных вычислениях, когда система массового обслуживания реализует ожидание заявки в очереди на обслуживание, но при этом, срок ожидания мал по сравнению со средним временем обслуживания одной заявки.
11.2.4 Рассмотрим примеры использования теории Эрланга для оценки вероятностей отказа на обслуживание и процент времени, когда система не загружена.
Пример 1. Автоматическая телефонная станция имеет 4 линии связи. На станцию поступает простейший поток заявок с интенсивностью вызовов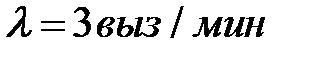 
. Вызов, поступивший на интервале времени, когда все линии заняты, получает отказ на обслуживание (короткие гудки). Среднее время занятости канала (средняя длительность телефонного разговора) 
. Приведенная к интервалу времени занятости канала плотность потока заявок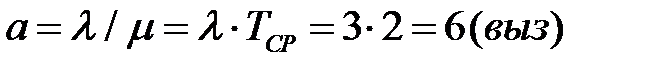 
.
Вероятность отказа на обслуживание определится из выражения:
.
Вероятность того, что станция окажется свободной, т.е. доля времени, в течение которой телефонная станция вообще не загружена, определится из выражения
.
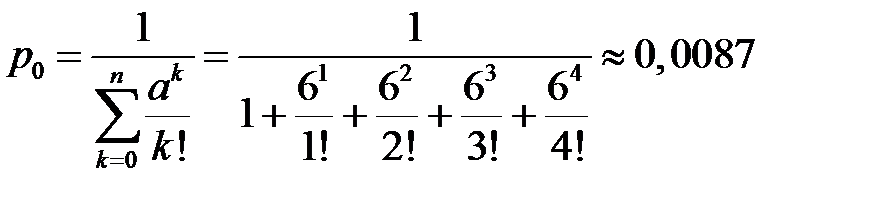Пример 2. В микросегментированной сети Ethernet коммутатор обрабатывает (коммутирует) пакеты данных без предварительной буферизации («на лету»). На три его порта из трех микросегментов могут независимо поступать пакеты, которые во времени не перекрываются и представляют собой поток заявок на обслуживание с интенсивностью 
. Каждый пакет в соответствии с таблицей коммутации пересылается на адресуемый выходной порт, в среднем, за время 
. При этом в каждый данный момент времени может коммутироваться только один пакет.
Вероятность того, что поступающий пакет не будет передан на адресуемый выходной порт (будет обслужен) определяется из выражения
.
Из этой формулы получим оценку вероятности отказа в обслуживании поступающего пакета от любого из трех микросегментов сети при условии, что все каналы окажутся занятыми, т.е.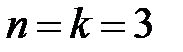 
, показатель закона распределения времени обслуживания заявки 
, приведенная плотность потока заявок, т.е. среднее число пакетов, приходящееся на среднее время обслуживания одного пакета 
,
.
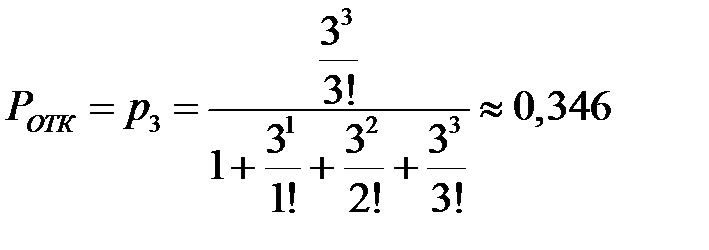11.2.5 Вторая концепция теории Эрланга (Erlang С) предполагает, что вызовы в системе могут удерживаться до тех пор, пока не обслужатся. То есть может быть сформирована очередь, что реализовано, в частности, во всех протоколах транкинговых радиосистем связи.
При этом в модели сети приняты следующие допущения:
– количество абонентов (пользователей) бесконечно велико;
– интервалы между вызовами случайные;
– длительность вызовов – величина случайная;
– время установления соединения ничтожно мало;
– вызов, поступивший первым в очередь, покидает её первым;
– ресурсы предоставляются в соответствие с порядком поступления запроса.
В этом случае вероятность удержания вызова (вероятность, что вызов будет поставлен в очередь)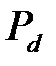 
вычисляется по формуле:
. (1)
Вероятность 
того, что удерживаемый вызов будет находиться в очереди время W, превышающее 
, определяется из выражения:
, (2)
где: 
– среднее время удержания канала в пересчете на одного абонента (в час наибольшей нагрузки);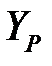 
– полезная нагрузка, которая может быть определена из выражения 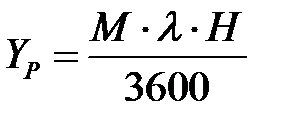(3)
, (3)
где, M – количество абонентов (терминалов); λ – количество вызовов на одного абонента в час наибольшей нагрузки (ЧНН).
Перемножая значения величин, определенные из выражений (1) и (2), можно рассчитать вероятность того, что любой вызов будет задержан на время большее, чем t:
. (4)
Эта величина характеризует качество обслуживания и ее называют вероятностью обслуживания.
На рисунке 11.2 приведены графики результатов сравнительного анализа качества обслуживания – значений вероятности обслуживания, для различных видов систем связи и числа каналов обслуживания. Полезная нагрузка на один канал приведена в Эрлангах.
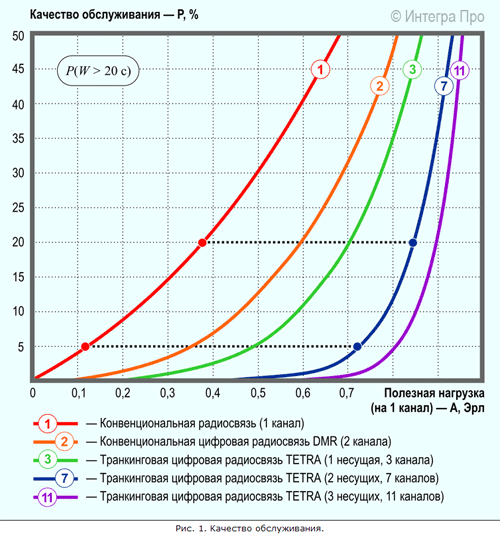
Рисунок 11.2 – Характеристики качества обслуживания систем радиосвязи
В соответствии со стандартом TETRA в системе транкинговой цифровой радиосвязи на одной несущей частоте организуется четыре логических канала, причем один из них является управляющим, а остальные предназначены для передачи речи или данных, при этом реализуется схема 1 + 3. В том случае, если базовая станция работает на двух несущих частотах, реализуется схема 1 + 7 (1 управляющий и 7 речевых каналов).
При расчетах нагрузки управляющий канал не учитывается. Стандарт DMR в конвенциональной (одноканальной) реализации поддерживает два логических канала на одной несущей частоте в отличие от аналоговой конвенциональной радиосвязи.
Один речевой канал с эффективной сигнальной системой может обеспечить не более чем 0.375 Эрл нагрузки с качеством обслуживания 20%. Это означает, что пользователи сети в час наибольшей нагрузки будут ожидать достаточно продолжительное время до тех пор, пока получат доступ к ресурсам (каналу).
Для сравнения, пропускная способность одного канала в семиканальной транкинговой системе, например, в системе стандарта TETRA на две несущих частоты – TetraFlex, фирмы DAMM Cellular Systems A/S, увеличится при таком же качестве обслуживания до 0,85 Эрл, то есть в 2,26 раза.
Если же требования к качеству обслуживания возрастают до уровня 5%, то преимущества семиканальной системы TETRA по отношению к одноканальной конвенциональной (в пересчете на один канал) будут еще более существенны. Можно видеть, что пропускная способность одного канала увеличится с 0,125 Эрл до 0,74 Эрл, то есть в 6 раз. Преимущества еще более заметны, когда количество разговорных каналов (каналов трафика) в системе возрастает.
Приведем расчет числа абонентов в сети с одним управляющим каналом и тремя каналами трафика (система TetraFlex с одной несущей) при следующих допущениях:
– cреднее время удержания канала (продолжительность вызова) в пересчете на одного абонента H = 20 с;
– среднее число вызовов на одного абонента в ЧНН λ = 5;
– количество каналов v = 3.
В этом случае полезная нагрузка на один канал составит 0,65 Эрл при качестве обслуживания 15%. Количество абонентов составит M = 23 на один канал (70 на всю сеть).
Cреднее время удержания задержанных вызовов, 
определяется из выражения
(5)
В свою очередь среднее время ожидания для всех вызовов 
определяется по формуле
(6)
На рисунке 11.3 приведены зависимости среднего времени удержания вызова в очереди в час наибольшей нагрузки в зависимости от величины полезной нагрузки (в пересчете на один канал) при условии, что качество обслуживания составляет 30%, среднее время удержания (занятия) канала 20 сек. Анализировались те же системы, что и приведенные на рисунке 11.2.
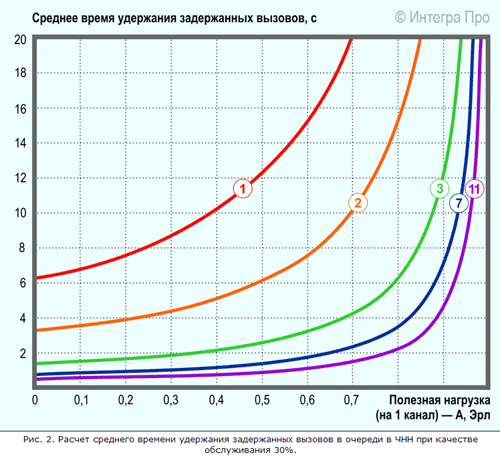
Рисунок 11.3 – Расчет среднего времени удержания вызовов в очереди в ЧНН при качестве обслуживания 30%.
Как следует из рассмотрения рисунка 11.3, среднее время удержания вызовов при полезной нагрузке на 1 канал величиной 0,5 Эрл при качестве обслуживания 30% уменьшится с 12 секунд (в одноканальной аналоговой конвенциональной системе) до 2,2 секунд (в цифровой системе TetraFlex на 3 речевых канала) и до 1,2 секунды (в семиканальной системе TETRA).