МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Институт высокоточных систем им. В.П. Грязева
Кафедра «Электроэнергетика»
Пояснительная записка курсовой работы
Учебной дисциплины (модуля)
«ИНФОРМАТИКА»
на тему:
«Методика и технология решения задач оптимизации в табличном процессоре Excel с помощью программы «Поиск решения» (Solver)»
Вариант 13
Выполнил:
студент группы Б161562 Розов Д.А.
Проверил:
доцент кафедры «Электроэнергетика»
___________________Горелов Ю.И.
Оценка_________________________
Дата ___________________________
Тула 2017 г.
Цель работы и задачи
Цель: освоение методики и технологии оптимизации планов в табличном процессоре Excel с помощью программы «Поиск решения» (Solver).
Задачи: составление наилучших (оптимальных) планов выпуска продукции; определение оптимального количества сотрудников в штате и т.д.
Задание 1. Оптимальный план выпуска продукции
Решить задачу оптимального плана выпуска объективов согласно варианту:
Предприятие решило производить два вида объективов А и В. Объектив вида А состоит из 3-х линзовых компонентов, вид В - из 4-х. За неделю можно изготовить не более определенного количества линз. На сборку объектива каждого вида требуется определенное количество времени.
Рабочая неделя для 4 сотрудников составляет 160 часов. Сколько объективов А и В надо изготовить, чтобы получить максимальную прибыль?
Исходные данные
| Вариант | Время сборки объектива | Стоимость объектива | Количество произведенных линз | ||
| А | В | А | В | ||
Решение.
Пусть надо изготовить Х (штук) объективов вида А, и У (штук) объективов вида В. Целевая функция (Р) - прибыль от продажи продукции, может быть рассчитана по формуле:
Р= 3400Х+4400У
Затраты на комплектацию(общее количество произведенных линз для обоих объективов) соответственно равны:
Zk = 3Х + 4У
Так как затраты времени на сборку объективов даны в минутах – необходимо перевести их в часы:
15 минут =0,25 часа, 20 минут = 0,33 часа.
Тогда затраты времени на производство объективов равны:
Zt = 0,25Х+0,33У
По условиям задачи комплектационные и временные ограничения составляют 1900 линз и 160 часов, поэтому
Zk = 3Х + 4У £ 1900,
Zt = 0,25Х+0,33У £ 160
Задача оптимизации плана выпуска объективов формулируется следующим образом:
Р= 3400Х+4400У ® max
при ограничениях
Zk = 3Х + 4У £ 1900,
Zt = 0,25Х+0,33У £ 160
Для решения этой задачи используем табличный процессор Excel и программу «Поиск решения».

В результате расчетов получено следующее решение:
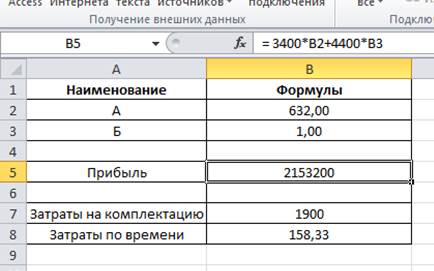
Вывод. Из решения видно, что оптимальный план выпуска объективов составляет 632 штук вида А и 1 шт. вида Б. При этом максимальная прибыль составит 2 153 200 рублей.
Задание 2. Оптимальное количество сотрудников в штате
Решить задачу определения оптимального количества сотрудников в штате согласно варианту:
Штат научно-исследовательской лаборатории (НИЛ) должен состоять из лаборантов, инженеров, младших научных сотрудников (м.н.с.), старших научных сотрудников (с.н.с.), ведущих научных сотрудников, и заведующего НИЛ.
Необходимо определить, учитывая общий месячный фонд зарплаты, какими должны быть оклады сотрудников НИЛ при условии, что оклад лаборанта не должен быть меньше прожиточного минимума 6 тыс.руб.
Инженер получает в 1,8 раза и на 600 руб. больше лаборанта. Младший научный сотрудник получает в 1,5 раза больше лаборанта и на 1100 руб. больше инженера. Старший научный сотрудник получает в 3,5 раза больше лаборанта. Ведущий научный сотрудник получает в 3,2 раза больше лаборанта, на 3200 руб. больше м.н.с. Заведующий НИЛ получает в 5 раз больше лаборанта.
| Вариант | Количество сотрудников | Фонд зар.платы | |||||
| лаборантов | инженеров | М.н.с. | С.н.с | В.н.с | Зав.НИЛ | ||
| 4..6 | 11..13 |
Решение. В основу для вычисления целевой функции возьмем оклад лаборанта (С), а остальные оклады будем вычислять, исходя из него – во сколько раз или на сколько больше оклада лаборанта.
В качестве математической модели этой задачи возьмем линейное уравнение, которое определяет общий месячный фонд зарплаты (Z):

где 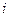 -количество должностей; Ni -число сотрудников в одной должности; С - оклад лаборанта; Ai- коэффициент, обозначающий во сколько раз оклад сотрудника больше оклада лаборанта; Bi- коэффициент, обозначающий на сколько раз оклад сотрудника больше оклада лаборанта.
-количество должностей; Ni -число сотрудников в одной должности; С - оклад лаборанта; Ai- коэффициент, обозначающий во сколько раз оклад сотрудника больше оклада лаборанта; Bi- коэффициент, обозначающий на сколько раз оклад сотрудника больше оклада лаборанта.
По условию задачи в отделе работают сотрудники на 6-ти должностях, поэтому i = [1..6]. N1- количество лаборантов; N2- количество инженеров; N3- количество младших научных сотрудников; N4- количество старших научных сотрудников; N5- количество ведущих научных сотрудников, N6- количество заведующих НИЛ, равное 1.
Так как инженер получает в 1,8 раза и на 600 руб. больше лаборанта, то А2=1,8; В2=600. Так как младший научный сотрудник получает в 1,5 раза больше лаборанта и на 1100 руб. больше инженера, то А3= 1,5; В3= В2+1100 = 1700.
Так как старший научный сотрудник получает в 3,5 раза больше лаборанта, то А4= 3,5; B4= 0. Так как ведущий научный сотрудник получает в 3,2 раза больше лаборанта, на 3200 руб. больше м.н.с., то А5= 3,2; В5= В3+3200 =4900.
Заведующий НИЛ получает в 5 раз больше лаборанта, тогда А6= 5; В6= 0.
Задача поиска оптимального количества сотрудников НИЛ может быть сформулирована следующим образом:
Z= 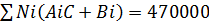
при ограничениях
4 £ N1 £ 6; 11 £ N2 £ 13; C ³ 6000
 Таблица исходных данных
Таблица исходных данных
Для решения этой задачи используем табличный процессор Excel и программу «Поиск решения».

В результате расчетов получено следующее решение:
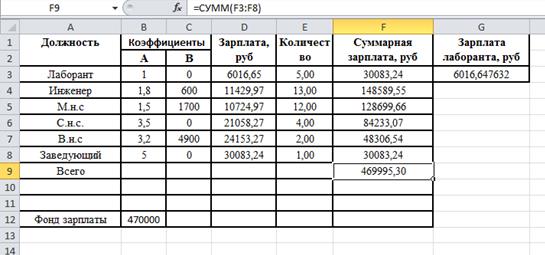
3 Решить задачу проектирования емкости согласно варианту:
Спроектировать емкость - параллелепипед с объемом V= abh= 3900 (длина, ширина, высота). Емкость должна иметь минимальную площадь стенок S = ab+ab+bh+bh+ah+ah
Задача оптимизации имеет вид
S = ab+ab+bh+bh+ah+ah®min
при ограничениях
V= abh= 3900
Таблица исходных данных
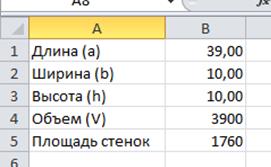
Для решения этой задачи используем табличный процессор Excel и программу «Поиск решения».
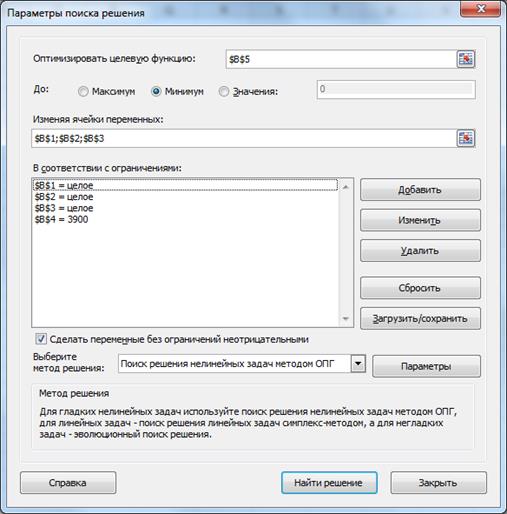
В результате расчетов получено следующее решение:
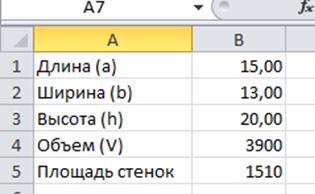
Решение:
| Длина | |
| Ширина | |
| Высота | |
| Площадь поверхности (min) | |
| Объем |
4 Решить задачу проектирования площади участка минимального периметра согласно варианту:
Участок имеет площадь S = аb = 880 м2. При какой длине (а) и ширине (b) периметр будет минимальным.
Периметр участка определяется по формуле
Р=2а+2b
Тогда задача минимизации периметра участка формулируется следующим образом
Р=2а+2b®min
при ограничении
S = аb = 880 м2.
Таблица исходных данных

Для решения этой задачи используем табличный процессор Excel и программу «Поиск решения».
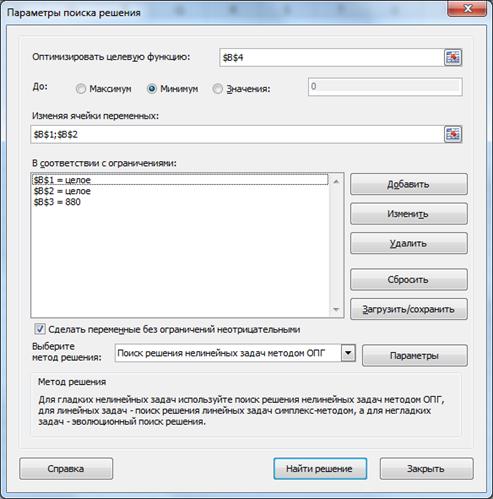
В результате расчетов получено следующее решение:
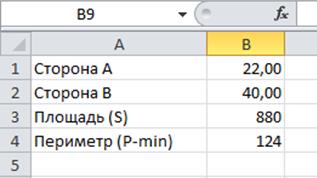
Решение:
| Сторона А | |
| Сторона B | |
| Площадь S | |
| Периметр P (min) |
Выводы
В ходе работы мною была освоена методика и технология оптимизации планов в табличном процессоре Excel с помощью программы «Поиск решения» (Solver).