Если n - простое число, то оно удовлетворяет сравнению an-1 mod n = 1 для любого a. В тесте выбирается m случайных чисел a и для каждого из них проверяется выражения an-1 mod n = 1. Если для всех ai (i = 1..m) выражение истинно, то вероятность того, что n составное число равна 1/2m.
Выполнение сравнения является необходимым, но не достаточным признаком простоты числа. Если хотя бы для одного a сравнение невыполнимо, то n составное, в противном случае ничего определенного сказать нельзя. Если для составного n выполняется сравнение an-1 mod n = 1, то число n называют псевдопростым по основанию a. Например, числа Кармайкла - составные числа, для которых сравнение an-1 mod n = 1 выполняется для всех a взаимно простых с n. Чисел Кармайкла - бесконечное множество, наименьшее число Кармайкла – 561 = 3 * 11 * 17.
Тест Миллера – Рабина.
Является модификацией теста Миллера и заключается в проверке только части свидетелей простоты b в интервале от 2 до n – 2, выбираемых случайным образом. Согласно недоказанной теореме Рабина, если тест Миллера, примененный к n для более, чем n / 4 свидетелей простоты, не распознает в n составного числа, то n – простое. Т.о. при положительной проверке m свидетелей простоты b вероятность того, что n составное число равна 1/4m. Рекомендуется брать m ≈ log2(n) (например, для n = 105 + 1, требуется проверить 13 свидетелей простоты).
Описание алгоритма.
1. Последовательно делим n – 1 на 2 пока не получим нечетное частное. В результате найдем положительное целое k и нечетное q, для которых n – 1 = 2k q.
2. Цикл А. Повторять m раз.
2.1. Выбрать случайно b в интервале 2.. n – 2.
2.2. x = bq mod n.
2.3. Если x = 1 или x = n – 1, то перейти на следующую итерацию цикла А.
2.4. Цикл В. Повторять k – 1 раз.
2.4.1. x = x2 mod n
2.4.2. Если x = 1, то выдать «n – составное число» и завершить работу.
2.4.3. Если x = n – 1, то перейти на следующую итерацию цикла А.
2.4.4. Перейти к следующей итерации цикла B.
2.5. Перейти к следующей итерации цикла А.
3. Выдать «n – вероятно простое».
Критерий Вильсона
Данный способ нахождения простого числа заключается в следующей теореме:
Натуральное число p > 1 является простым тогда и только тогда, когда (p –1)!+1 делится на p.
Тест Соловея–Штрассена
Заключается в следующем:
1. Выбираем случайное число a из интервала [1; n -1] и проверяем с помощью алгоритма Евклида условие НОД(a,n)=1.
2. Если оно не выполняется, то n – составное.
3. Проверяем выполнимость сравнения:
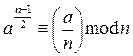 .
.
4. Если оно не выполняется, то n – составное.
5. Если сравнение выполнено, то ответ неизвестен (и тест можно повторить еще раз).
Сложность данного теста, как и теста на основе малой теоремы Ферма, оценивается величиной O(log3n).
Данный тест полностью аналогичен тесту на основе малой теоремы Ферма, однако, он обладает решающим преимуществом – при его использовании возникает только две ситуации:
– число n простое и тест всегда говорит «не известно»;
– число n составное и тест с вероятностью успеха не меньше 1/2 дает ответ «n – составное».
После повторения теста k раз вероятность неотбраковки составного числа не превосходит 1/2k.
Разложение числа на простые сомножители
Представление натурального числа в виде произведения простых называется разложением числа на простые сомножители или факторизацией числа. На настоящий момент неизвестны полиномиальные алгоритмы факторизации чисел, хотя и не доказано, что таких алгоритмов не существует. На предполагаемой большой вычислительной сложности задачи факторизации базируется криптосистема RSA и некоторые другие. Факторизация с полиномиальной сложностью теоретически возможна на квантовом компьютере с помощью алгоритма Шора.
В зависимости от сложности алгоритмы факторизации можно разбить на две группы. Первая группа – экспоненциальные алгоритмы, сложность которых экспоненциально зависит от длины входящих параметров (т.е. от длины самого числа в бинарном представлении). Вторая группа – субэкспоненциальные алгоритмы.
A. Экспоненциальные алгоритмы:
- метод факторизации Ферма;
- ρ-алгоритм Полларда;
- ρ-1 алгоритм Полларда;
Б. Субэкспоненциальные алгоритмы:
- метод непрерывных дробей (CFRAC);
- метод квадратичного решета;
- метод эллиптических кривых;
- общий метод решета числового поля (считается самым быстрым алгоритмом на текущий момент);
Рассмотрим три экспоненциальных алгоритма.