Исследование функции на монотонность.

- Найдите область определения функции;

- Найдите производную фун и область определения производной;

- Найдите значение аргумента, при которых производная равна нулю;

- Определите знаки производной на каждом из полученных промежутков;

- По знакам производной определите, на которых промежутках функция возрастает, а на каких спадает;

 

 

17.Признаки выпуклости и вогнутости функции

Граф фун у=f(х) называется упуклым вниз на некотором интервале [a.b] если он расположен выше любой ее касательной на этом интервале.

Граф фун у=f(х) назыв выпуклым вверх на итерваде а,в если он расположен ниже любой касательной на этом интервале

Свойства выпуклых функций:

1. Хорда, соединяющая две любые точки кривой графика выпуклой фун, всегда проходит над кривой в интервале между двумя этими точками.
2. Выпуклая функция лежит над своими касательными
3. Вторая производная f(x) всегда не отрицательна на рассматриваемом интервале.
4. Для выпуклой функции локальный минимум всегда является глобальным минимумом.

Функция f(x₁,:,x_n) является вогнутой функцией на множестве D тогда и только тогда, когда -f(x) есть выпуклая функция на D

 

 

18.Точки перегиба. Необходимые и достаточное условие перегиба

Т. Если вторая производная f’’(х) при переходе через точ х₀, в которой она равнв нулю или не существует меняет знак,то точ графика фун с координатой х₀,у₀ есть точ перегиба.

Если функция непрерывна в точке и имеет в этой точке конечную или бесконечную производную и если меняет знак при переходе через точку, то точка - точка перегиба функции.

 

 

19.правило исследования фун на выпуклость, вогнутость и перегиб

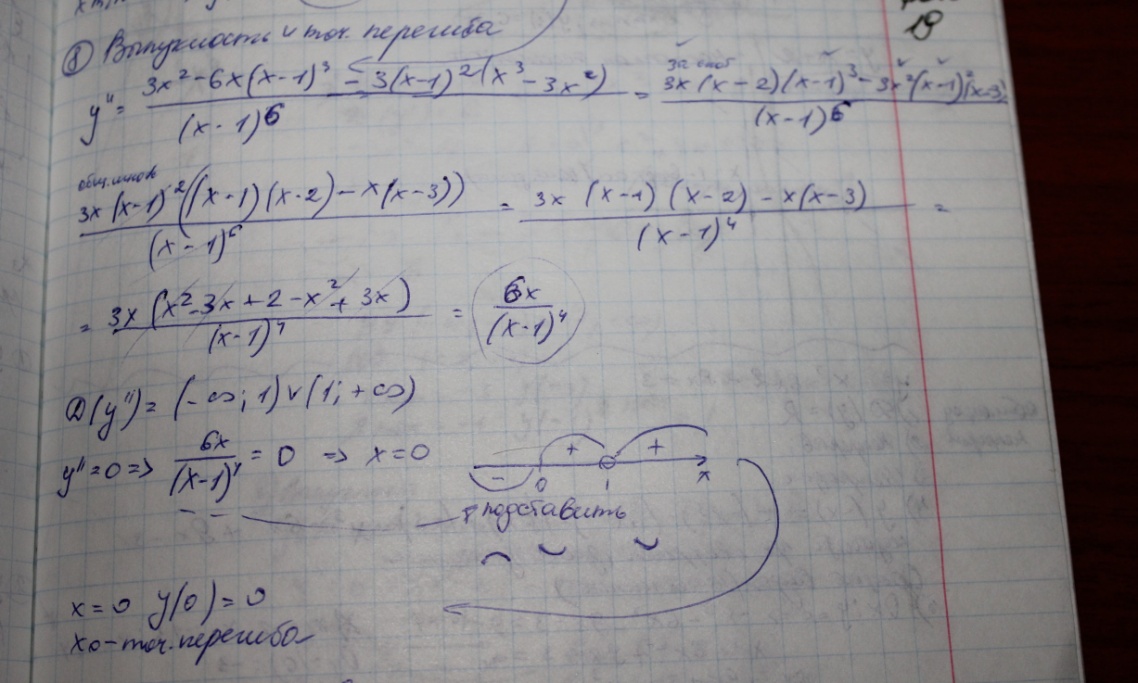
20.Асимптоты функции, их виды и способы нахождения

Асимптоты кривой назыв прямыми, расстояние до кот от точ,лежащей на кривой стримитс к нулю при неограниченном удалении от начала координат этой точ по кривой.

Виды асимптот:вертикальные, наклонные, горизонтальные

Прямая х=а назыв вертикальной асимптотой графика фун у=f(х) только тогда,когда односторонние пределы(хотя бы 1) равен ∞

Для определения наклонных асимптот требуется вычислить 2 предела,т.к. любая асимптота есть прямая,то она у=кх+в, к и в определяем по формулам

*1 чтобы асимптота стала горизотальной надо чтобы к=0,тогда у=в

*2 если хотя бы 1 из пределов не существует или равен ∞, то наклонных(горизонтальных) асимптот нет

*3 для фун, содержащих е в некоторой степени надо рассматривать пределы и при х стремится к ∞

 

 

21.нахождение наибольшего и наименьшего значения функции и на промежутке

чтобы найти наибольшее или наименьшее значение функции на отрезке, нужно исследовать поведение функции на данном отрезке с помощью производной.

следуем алгоритму:

1. Находим ОДЗ функции.

2. Находим производную функции

3. Приравниваем производную к нулю

 

4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:

Если на промежутке I производная функции, то функция возрастает на этом промежутке.

Если на промежутке I производная функции, то функция убывает на этом промежутке.

5. Находим точки максимума и минимума функции.

В точке максимума функции производная меняет знак с «+» на «-».

В точке минимума функции производная меняет знак с «-» на «+».

6. Находим значение функции в концах отрезка,

§ затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции

§ или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции

22.Первообразная функции. Неопределенный интеграл и его свойства

Перообразная фун F(х) назыв первообраз для фуну=f(x) на промежутке (а,в),если для любого х из этого промежутка выполняются условия F’(x)=f(x)

f(x)=х²

F(х)=х³/3

Фото

Т.множество всех первообраз для фун у=f(x) можно записатьF(х)+с, где с-константа

 

Сво-во неопределенного интеграла

-постоянный множитель выносится за знак интеграла \

 

 

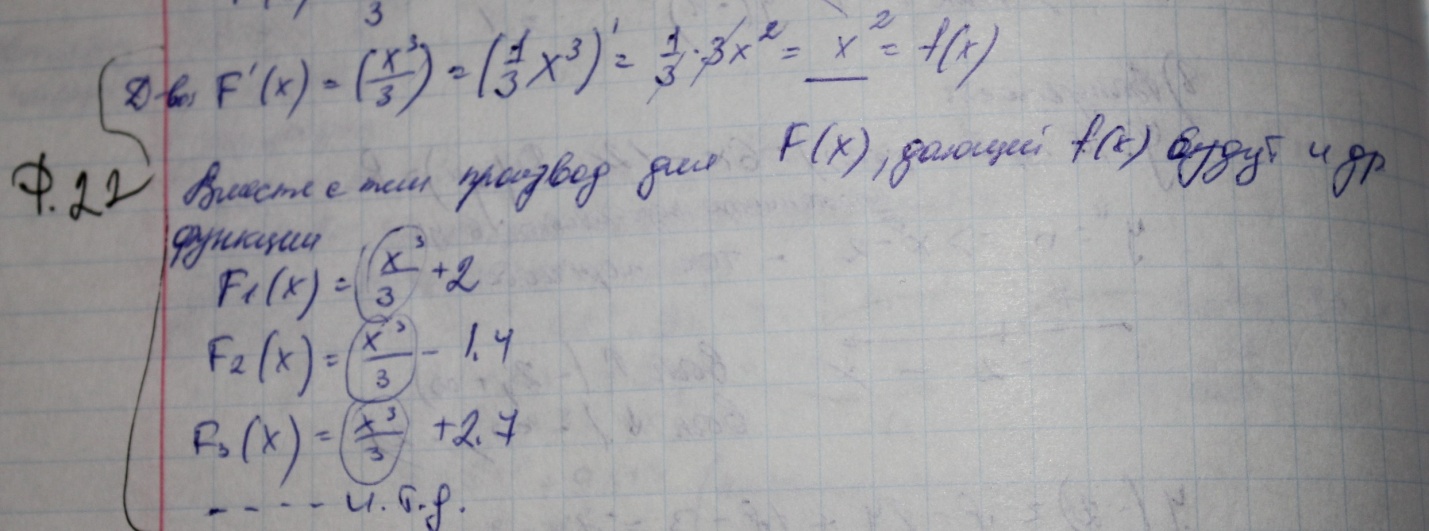
23.таблица основых интегралов

 

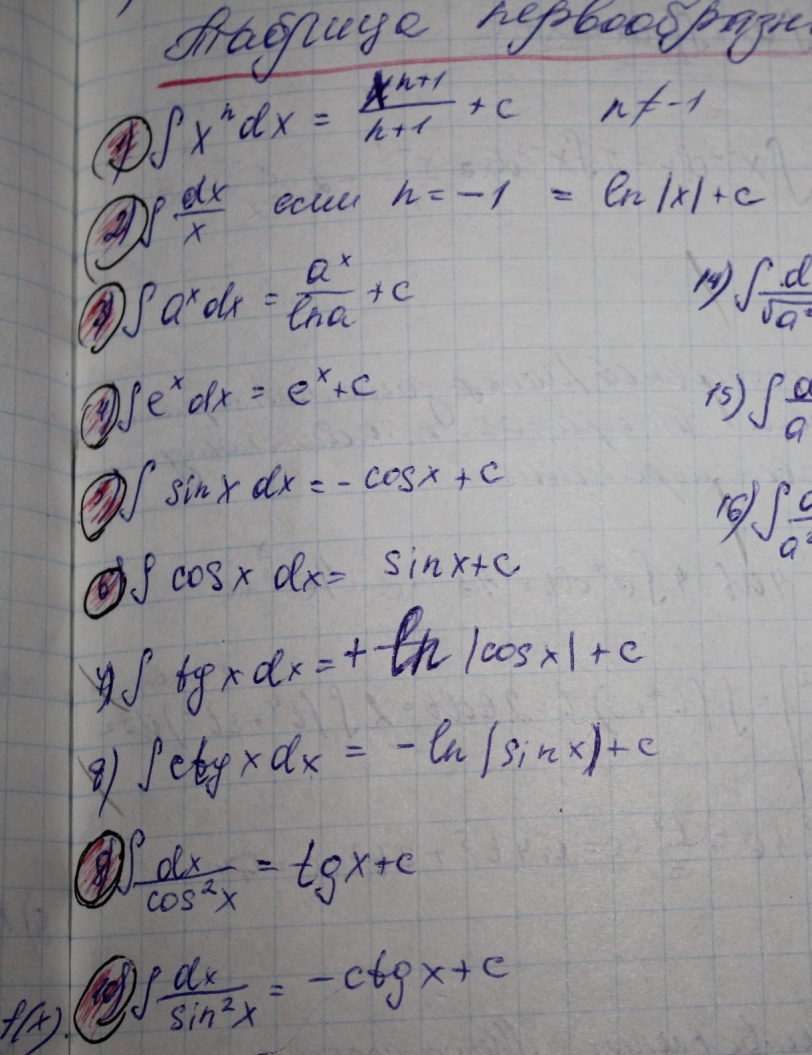
24.методы интегрирования: непосредственное интегрирование, интегрирование постановкой

Метод интерирования постановкой основан на приведении интегралов к табличному с помощью введения новой переменной

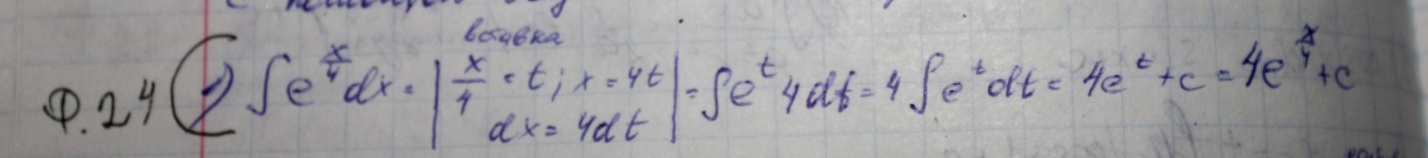
Непосредственное интегрирование. Метод состоит из 2х разновидностей: создается на базе под интегральной фун алгебраическими преобразованиями табличный интеграл

И второй искусственно изменяет дифференциал создается табличный интеграл

 

25. интегрирование по частям

Известна формула (uv)’=u’v+v’u ее можно записать,если использовать дифференциалы d(uv)=vdu+udv. Выразим из этого выраж u на dv

Udv= d(uv)- vdu. Преинтегрируем левую и правую части последнего равенства

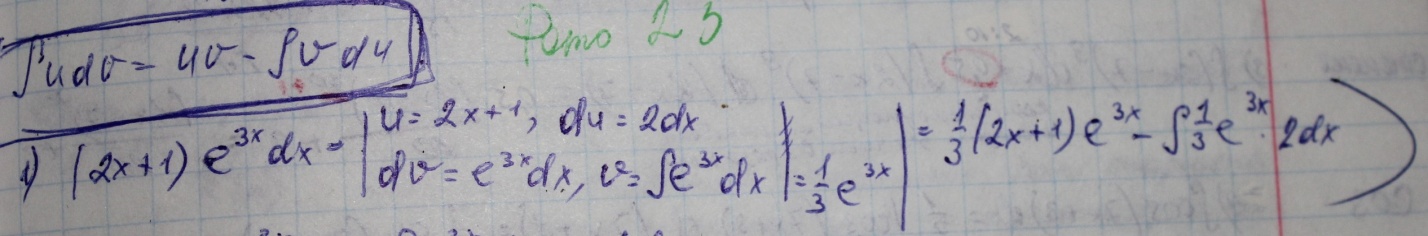
26 Определенный интеграл, его геометрический смысл. Свойства определенного интеграла. Формула Ньютона-Лейбинца.

Определённый интеграл 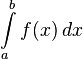численно равен площади фигуры, ограниченной осью абсцисс, прямыми х=а и х=в и графиком функции y=f(x)

 

Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.

 

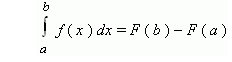
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x), вычислить ее значения в точках a и b и найти разность F(b) – F(a).

 

27.Приложения определенного интеграла к вычислению площадей плоских фигур.

(ПРОЙДИ ПО ССЫЛКЕ!) https://ucmok.ru/matan/gifp.pdf только то, что под буквой А)

 

28.несобственный интеграл с бесконечными пределами интегрирования.

Несобственный интеграл от функции f (x) в пределах от а до ∞ определяется равенством

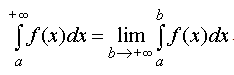
Если предел существует и конечен, то несобственный интеграл называется сходящимся. Если предел не существует или равен бесконечности, то интеграл называется расходящимся. Эти правила действуют и в других случаях, когда бесконечным является нижний предел интегрирования или оба предела интегрирования бесконечны:

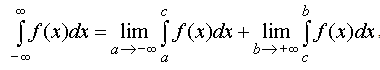
29.Диффернециальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка

Дифференциальное уравнение первого порядка, содержит:
1) независимую переменную ;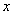
2) зависимую переменную 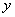(функцию);
3) первую производную функции: .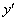

Они бывают:

Диф урав с раздельными переменными

С разделяющимися переменными

Однородные

Линейные

 

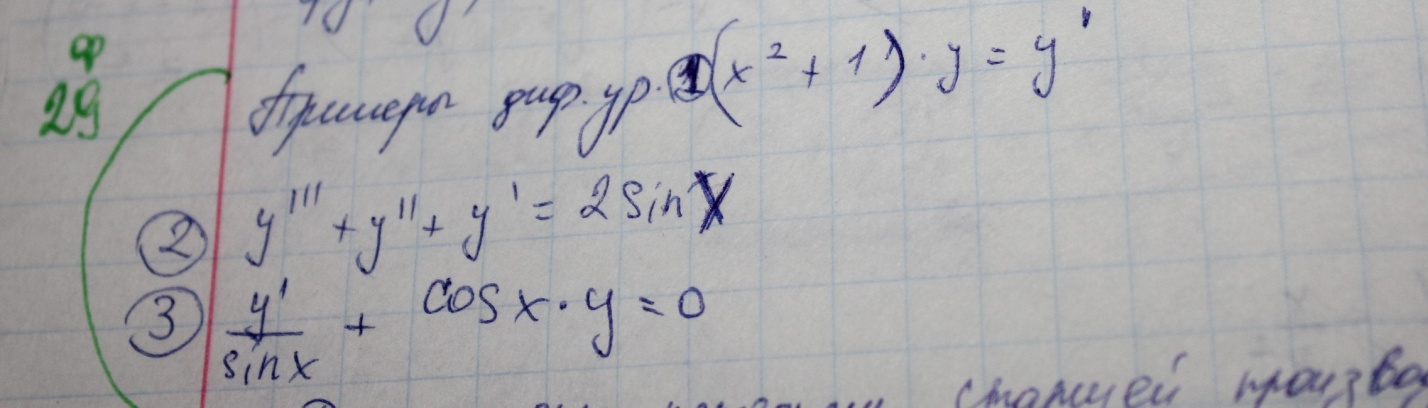
30. диффернциальне уравнения с разделяющимися переменными

Уравнение вида Р1(х) *g1(y)dx+P2(x)*g2(y)dy=0

Диф урав с разделяющ переменными легко превращ в диф урав с раздельными переменными для этого надо обе части урав разделить на те множители, которые мешают каждому дифференциалу

 

 

31.Однородные дифференциальные уравнения

Диф урав 1 порядка назыв однородными, если все переменные с фун можно связать друг с другом виде х/у. Решение такого примера оснвано на подстановке вида

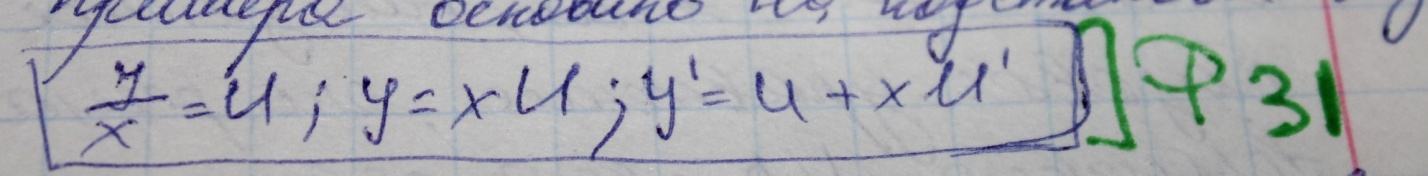
В результате такой подстановки диф урав имеет вид урав с раздельными переменными

 

 

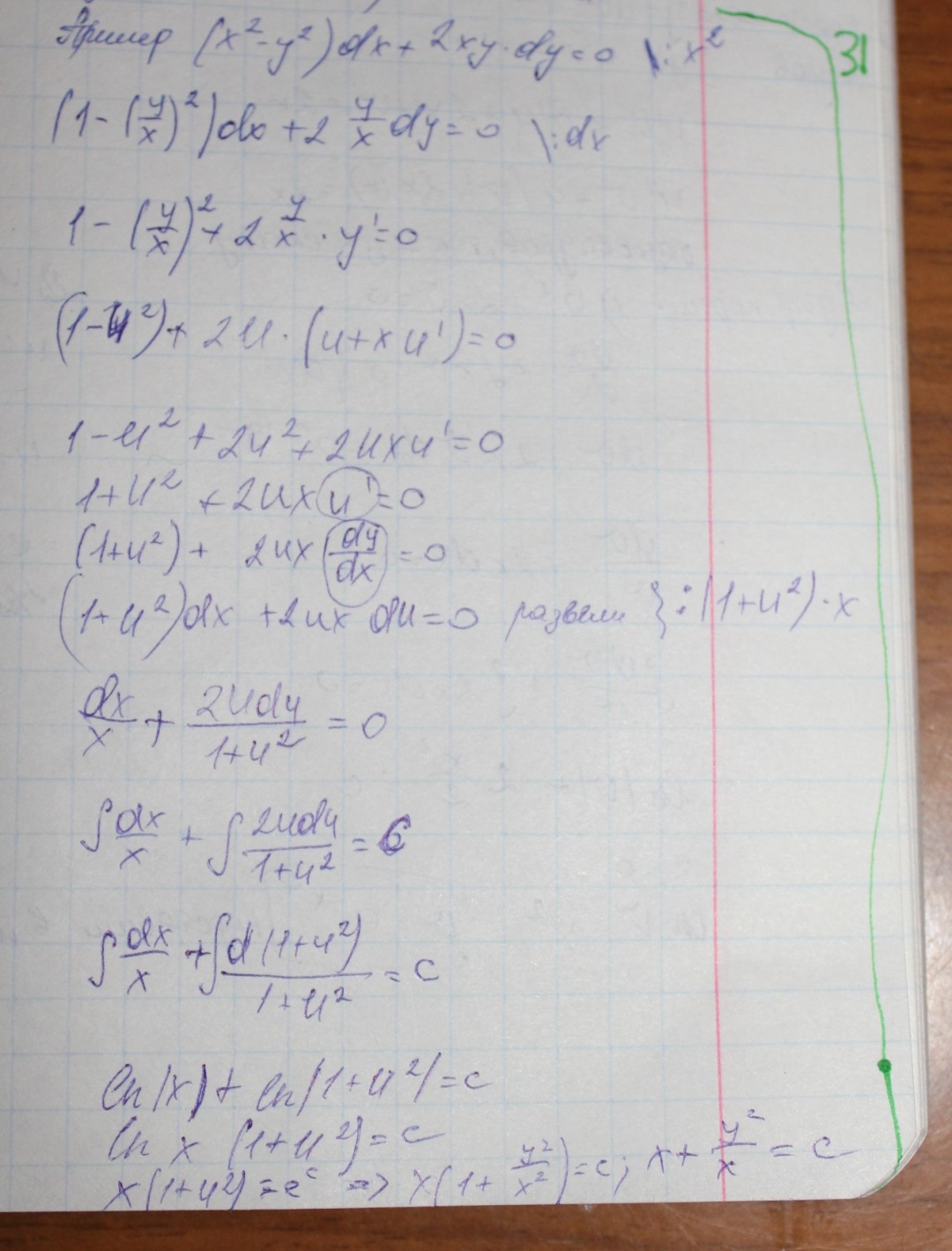
32.Линейные дифференциальные уравнения

 

 

33. Дифференциальные уравнения высших порядков

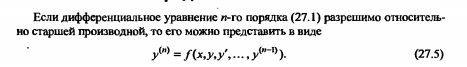
34.Диф урав допускающие понижение порядка вида y’’=f(x)

Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде:

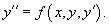
Уравнение вида y''= f (x)

Если дано уравнение y'' = f (x), то его порядок можно понизить введением новой функции p (x), такой, что y' = p (x). В результате мы получим дифференциальное уравнение первого порядка

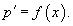
Решая его, находим функцию p (x). Затем решаем второе уравнение

и получаем общее решение исходного уравнения.

 

35. Диф урав допускающие понижение порядка вида y’’=f(x;y’)

Уравнение вида y''= f (x,y' )

Используем подстановку y' = p (x), где p (x) − новая неизвестная функция, и получаем уравнение первого порядка

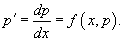
Интегрируя, определяем функцию p (x). Далее решаем еще одно уравнение 1-го порядка

и находим общее решение y (x).

 

36.Числовые ряды. Основные понятия. Ряд геометрической прогрессии

Числовой ряд – это сумма членов числовой последовательности вида .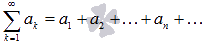

Частичная сумма числового ряда – это сумма вида 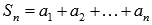, где n – некоторое натуральное число. S_n называют также n-ой частичной суммой числового ряда.

К примеру, четвертая частичная сумма ряда 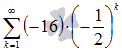есть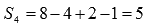

 

Т. Ряд геометрической прогрессии сходится, если ее знаменатель меньше единицы и расходится, если модуль у знаменателя больше чем равен одному

 

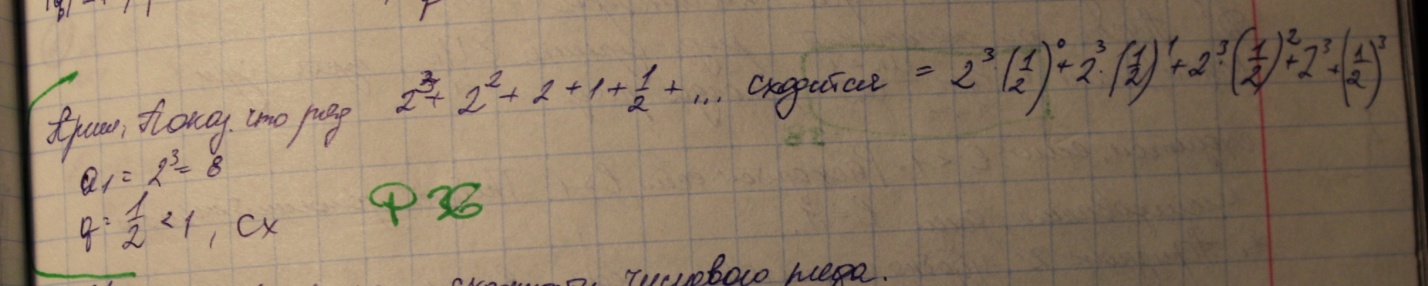
37.необходимый признак сходимости числового ряда. Гармонический ряд.

Необходимый признак сходимости числового ряда.

Нахождение частичной суммы ряда является сложной задачей для ее решения. Сущ признаки сходимости, главными из наих является необходимый признак сходимости.

Это есть признак,если ряд 1 сходтся,то предел его общего числа равен 0

Необходимый признак сходимости однозначно не говорит сходимости нет данный ряд, поэтому во многих случиях можно определить с помощью достаточных признаков

гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда:

.

 

 

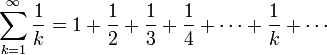
38.Признаки сравнения рядов. Признак Даланбера

Признак сравнения ряда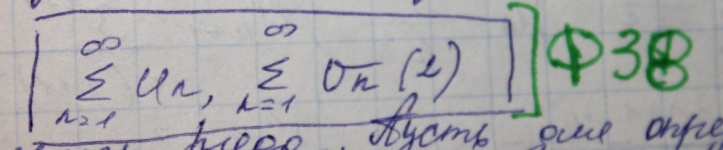

Т1. Даны 2 закономерных ряда. Пусть для определенности Un меньше или равно Vn, тогда из сходимости ряда 2 следует сходимость ряда 1. Из расходимости ряда 1 следует расходимость ряда 2.

Пусть даны 2 закономерных ряда 1 и 2, если существует конечный предел их отношений, то тогда оба ряда сходятся или расходятся одновременно

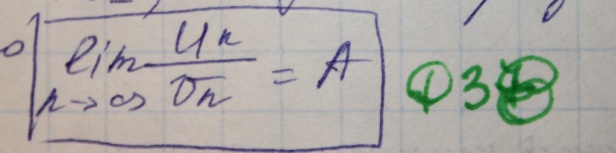
Призанк Даланбера

Пусть дан ряд суммы ЕUn (над Е бесконечность,под н=1), пусть существует предел отношений ,тогда ряд сходится, если L меньше 1. Расходится если L больше 1. Требует дополнительного исследования,если л = 1

*1. Признак Д-ра удобно использовать если в записи есть факториал и степень

*2. При дополнительно исследовании если в записи есть факториал и степень

39.Радикальный признак Коши. Интегральный признак Коши

Радикальный.

Пусть дан ряд со законоположительными членами,тогда если существует

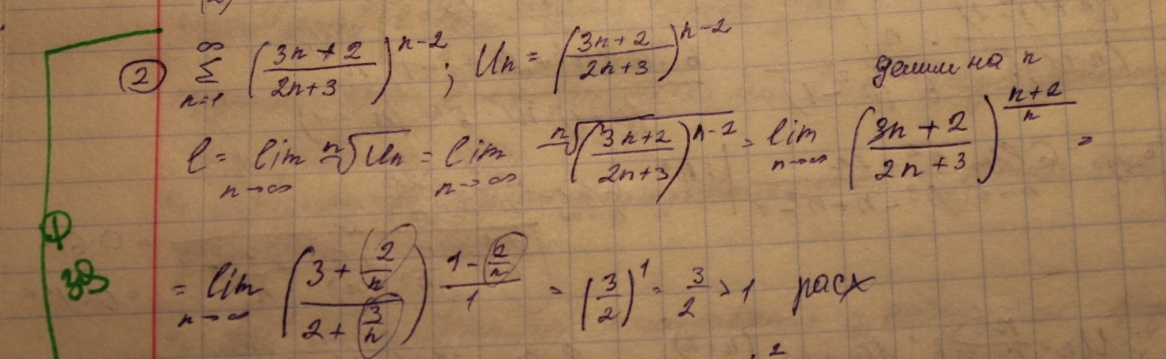
Интегральный признак Коши

Интегральный признак Коши́-Макло́рена — признак сходимости убывающего положительного числового ряда. Признак Коши даёт возможность свести проверку сходимости ряда к проверке сходимостинесобственного интеграла соответствующей функции на [1,∞) последний часто может быть найден в явном виде.

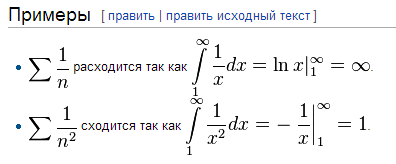
40.знакочередующиеся ряды. Признак лейбница. Общий достаточный признак сходимости знакопеременных рядов

Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится.

Или в два пункта:

1) Ряд является знакочередующимся.

2) Члены ряда убывают по модулю: 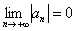. Причём, убывают монотонно.

Если выполнены оба условия, то ряд сходится.

В условиях теоремы Лейбница должна выполняться монотонность убывания (неважно, строгая или нестрогая). При этом члены ряда могут даже некоторое время возрастать по модулю, но «хвост» ряда обязательно должен быть монотонно убывающим.

 

41.абослютная и условная сходимости числовых рядов

-знакопеременный ряд называется абсолютно сходящимся,если ряд составленный из модулей и его членов сходится

-знакопеременный ряд называется условно сходящимся,если сам он сходится, в ряд, составленный из модулей и его членов- расходится

42. основные понятия.. Теорема Абеля. интервал и радиус сходимости степенного ряда.

Теорема Аблеля