Конспект урока
Тема №9. Перпендикулярность плоскостей
Теоретический материал для самостоятельного изучения
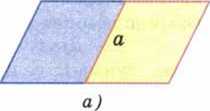
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей в виде прямой а, не принадлежащими одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями. Прямая а, которая является общей границей полуплоскостей, называется ребром двугранного угла (рис. 1а и 1б).
Двугранный угол с ребром CD, на разных гранях которого отмечены точки A и B называют двугранным углом CABD.
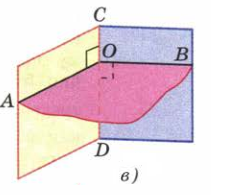
Перпендикуляры к ребру AO и BO образуют линейный угол двугранного угла AOB (рис. 1в). Так как луч ОА перпендикулярен прямой CD и луч OB перпендикулярен прямой CD, то плоскость АОВ перпендикулярна к прямой CD. Таким образом, плоскость линейного угла перпендикулярна к ребру двугранного угла. Двугранный угол имеет бесконечное множество линейных углов
Градусной мерой двугранного угла называется градусная мера его линейного угла. Так же как и плоские углы, двугранные углы могут быть прямыми, острыми и тупыми.
Все линейные углы двугранного угла равны друг другу.
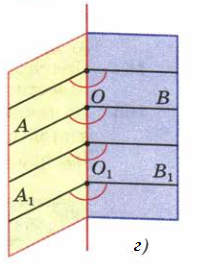
Рассмотрим два линейных угла АОВ и А1О1В1 (рис. 1г). Лучи ОА и О1А1, лежат в одной грани и перпендикулярны к прямой ОО1, поэтому они сонаправлены. Точно так же сонаправлены лучи OB и O1B1. Поэтому углы АОВ и А1О1В1 равны как углы с сонаправленными сторонами.

(Рис. 1)
Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.
Если один из этих двугранных углов равен фи, то другие три угла равны соответственно 180 градусов минус фи, фи и 180 градусов минус фи (рис. 2 а). В частности, если один из углов прямой, то и остальные три угла прямые. Если угол между пересекающимися плоскостями равен 90 градусом, будем называть такие плоскости перпендикулярными (рис. 2б).
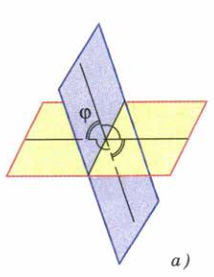
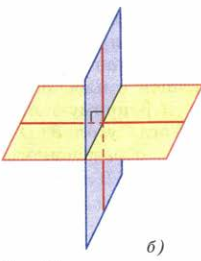
(Рис. 2)
Для доказательства теоремы рассмотрим плоскости альфа и бетта такие (рис. 3), что плоскость альфа проходит через прямую АВ, перпендикулярную к плоскости бетта и пересекающуюся с ней в точке А. Докажем, что плоскости альфа и бетта перпендикулярны. Плоскости альфа и бетта пересекаются по некоторой прямой АС. При этом прямая АВ перпендикулярна прямой АС, так как по условию прямая АВ перпендикулярна плоскости бетта, это означает, что прямая АВ перпендикулярна к любой прямой, лежащей в плоскости бетта.
Проведем в плоскости бетта прямую AD, перпендикулярную к прямой АС. Тогда угол BAD — линейный угол двугранного угла, образованного при пересечении плоскостей альфа и бетта. Но угол BAD равен 90 градусов так как прямая АВ перпендикулярна плоскости бетта. Следовательно, угол между плоскостями альфа и бетта равен 90 градусов. Что и требовалось доказать.
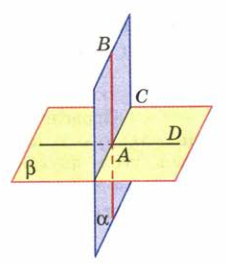
(Рис. 3)
Из этой теоремы вытекает важное следствие:
Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
| На рисунке 4 представлен прямоугольный параллелепипед. У этой фигуры все боковые ребра перпендикулярны основанию. Его основаниями служат прямоугольники ABCD и A1B1C1D1, а боковые ребра АА1,BB1,CC1 и DD1 перпендикулярны к основаниям. Отсюда следует, что ребро АА1 перпендикулярно к ребру АВ, т. е. боковая грань АА1В1В является прямоугольником. То же самое можно сказать и об остальных боковых гранях. |
| Таким образом, прямоугольный параллелепипед обладает следующими свойствами: 1) В прямоугольном параллелепипеде все шесть граней — прямоугольники. 2) Все двугранные углы прямоугольного параллелепипеда — прямые. 3) Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Измерениями прямоугольного параллелепипеда называются длины трех ребер, имеющих общую вершину. Докажем последнее свойство. |
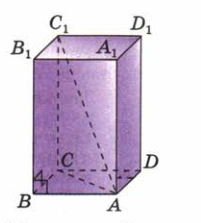
(Рис. 4)
Так как ребро СС 1 перпендикулярно к основанию ABCD, то угол АСС 1, прямой. Из прямоугольного треугольника АСС 1, по теореме Пифагора получаем
АС 1 2 равно АС2 + СС 1 2.
Но АС — диагональ прямоугольника ABCD, поэтому АС2 равно АВ2 + АD2. Кроме того, ребро СС 1 равно ребру АА 1. Следовательно, AC 1 равно АВ2 + AD2 + АА 1 2. Что и требовалось доказать.
Следствием из этого свойства является то, что диагонали прямоугольного параллелепипеда равны.
Стоит отметить, что если у прямоугольного параллелепипеда все три измерения равны, то он называется, а все его грани являются равными друг другу квадратами.