Простейшим методом минимизации функции одной переменной, не требующим вычисления производной, является метод деления отрезка пополам. Опишем его, предполагая, что минимизируемая функция J(и) унимодальна на отрезке [a, b]. Поиск минимума J(и) на [а, b] начинается с выбора двух точек 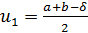 и
и 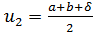 , где
, где 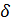 — постоянная, являющаяся параметром метода, 0 <
— постоянная, являющаяся параметром метода, 0 < 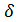 < b – a. Величина
< b – a. Величина 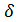 выбирается вычислителем и может определяться целесообразным количеством верных десятичных знаков при задании аргумента
выбирается вычислителем и может определяться целесообразным количеством верных десятичных знаков при задании аргумента 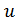 . В частности, ясно, что
. В частности, ясно, что 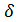 не может быть меньше машинного нуля ЭВМ, используемой при решении рассматриваемой задачи. Точки
не может быть меньше машинного нуля ЭВМ, используемой при решении рассматриваемой задачи. Точки 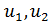 расположены симметрично на отрезке [ a, b ] относительно его середины и при малых
расположены симметрично на отрезке [ a, b ] относительно его середины и при малых 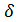 делят его почти пополам — этим и объясняется название метода.
делят его почти пополам — этим и объясняется название метода.
После выбора точек 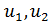 вычисляются значения J(
вычисляются значения J(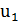 ), J(
), J(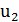 ) и сравниваются между собой. Если J(
) и сравниваются между собой. Если J(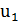 )≤ J(
)≤ J(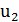 ), то полагают
), то полагают  = a,
= a, 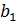 = u2; если же J(
= u2; если же J(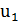 )>J(
)>J(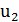 ) то полагают
) то полагают  =
= 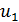 ,
, 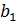 =b. Поскольку J(и) унимодальна на [a, b], то ясно, что отрезок [
=b. Поскольку J(и) унимодальна на [a, b], то ясно, что отрезок [ 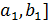 , имеет общую точку с множеством
, имеет общую точку с множеством 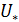 точек минимума J(u) на [a, b] и его длина равна
точек минимума J(u) на [a, b] и его длина равна
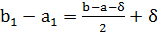 .
.
Пусть отрезок 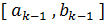 , имеющий непустое пересечение с
, имеющий непустое пересечение с 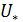 , уже известен, и пусть
, уже известен, и пусть 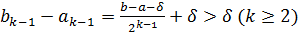 . Тогда берем точки
. Тогда берем точки 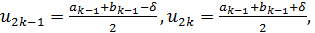 расположенные на отрезке
расположенные на отрезке 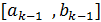 , симметрично относительно его середины, и вычисляем значения
, симметрично относительно его середины, и вычисляем значения 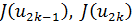 . Если
. Если 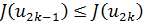 , то полагаем
, то полагаем 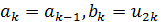 ; если же
; если же 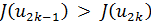 , то полагаем
, то полагаем 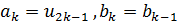 .
.
Длина получившегося отрезка 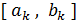 равна
равна 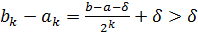 и [
и [ 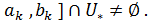
Если количество вычислений значений минимизируемой функции ничем не ограничено, то описанный процесс деления отрезка пополам можно продолжать до тех пор, пока не получится отрезок 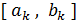 длины
длины 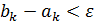 , где
, где 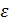 — заданная точность,
— заданная точность, 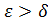 . Отсюда имеем, что к > log2 ((
. Отсюда имеем, что к > log2 ((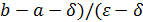 )). Поскольку каждое деление пополам требует двух вычислений значений функции, то для достижения точности
)). Поскольку каждое деление пополам требует двух вычислений значений функции, то для достижения точности 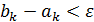 требуется всего
требуется всего 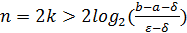 таких вычислений.
таких вычислений.
После определения отрезка 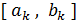 в качестве приближения ко множеству
в качестве приближения ко множеству 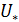 можно взять точку
можно взять точку 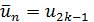 при
при 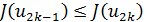 и
и 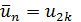 при
при 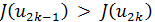 , а значение
, а значение 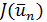 может служить приближением для
может служить приближением для 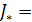 . При таком выбореприближения для
. При таком выбореприближения для 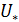 будет допущена погрешность
будет допущена погрешность 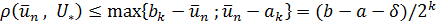 . Если не требовать того, чтобы значение функции, принимаемое за приближение к
. Если не требовать того, чтобы значение функции, принимаемое за приближение к 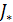 , было вычислено непременно в той же точке, которая служит приближением к
, было вычислено непременно в той же точке, которая служит приближением к 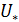 , то вместо
, то вместо 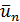 можно взять точку
можно взять точку 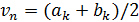 с меньшей погрешностью
с меньшей погрешностью 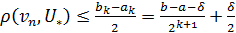 (здесь к = п/2 и
(здесь к = п/2 и 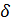 достаточно мало).
достаточно мало). 
Конечно, и в этом случае можно бы провести еще одно дополнительное вычисление значения функции в точке 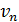 и принять
и принять 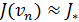 Однако заметим, что на практике нередко встречаются функции, нахождение значения которых в каждой точке связано с большим объемом вычислений или дорогостоящими экспериментами, наблюдениями,— понятно, что здесь приходится дорожить каждым вычислением значения минимизируемой функции. В таких ситуациях возможно даже, что число
Однако заметим, что на практике нередко встречаются функции, нахождение значения которых в каждой точке связано с большим объемом вычислений или дорогостоящими экспериментами, наблюдениями,— понятно, что здесь приходится дорожить каждым вычислением значения минимизируемой функции. В таких ситуациях возможно даже, что число 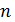 , определяющее количество вычислений значений функции, заранее жестко задано и превышение его недопустимо.
, определяющее количество вычислений значений функции, заранее жестко задано и превышение его недопустимо.
Из предыдущего следует, что методом деления отрезка пополам с помощью 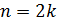 вычислений значений функции можно определить точку минимума унимодальной функции на отрезке
вычислений значений функции можно определить точку минимума унимодальной функции на отрезке 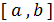 в лучшем случае с точностью
в лучшем случае с точностью 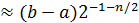 . Возникает вопрос, не существует ли методов, позволяющих с помощью того же числа вычислений значений функции решить задачу минимизации унимодальной функции поточнее? Оказывается, такие методы есть. Один из них будет описан в § 4.
. Возникает вопрос, не существует ли методов, позволяющих с помощью того же числа вычислений значений функции решить задачу минимизации унимодальной функции поточнее? Оказывается, такие методы есть. Один из них будет описан в § 4.
В заключение отметим, что метод деления отрезка пополам без изменений можно применять для минимизации функций, не являющихся унимодальными. Однако в этом случае нельзя гарантировать, что найденное решение будет достаточно хорошим приближением к глобальному минимуму,
§ 4. Метод золотого сечения. Симметричные методы
Перейдем к описанию метода минимизации унимодальной функции на отрезке, столь же простого, как метод деления отрезка пополам, но позволяющего решить задачу с требуемой точностью при меньшем количестве вычислений значений функции. Речь пойдет о методе золотого сечения.
1. Как известно, золотым сечением отрезка называется деление отрезка на две неравные части так, чтобы отношение длины всего отрезка к длине большей части равнялось отношению длины большей части к длине меньшей части отрезка.
Нетрудно проверить, что золотое сечение отрезка 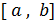 производится двумя точками
производится двумя точками 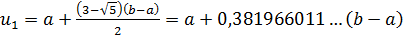 и
и 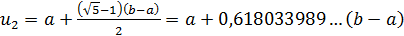 ,расположенными симметрично относительно середины отрезка, причем
,расположенными симметрично относительно середины отрезка, причем 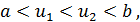
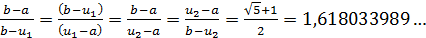
Замечательно здесь то, что точка 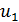 в свою очередь производит золотое сечение отрезка
в свою очередь производит золотое сечение отрезка 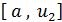 , так как
, так как 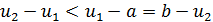 и
и 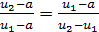 . Аналогично точка
. Аналогично точка 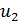 производит золотое сечение отрезка
производит золотое сечение отрезка 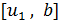 . Опираясь на это свойство золотого сечения, можно предложить следующий метод минимизации унимодальной функции
. Опираясь на это свойство золотого сечения, можно предложить следующий метод минимизации унимодальной функции 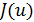 на отрезке
на отрезке 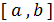 .
.
Положим 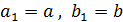 . На отрезке
. На отрезке 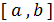 возьмем точки
возьмем точки 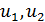 , производящие золотое сечение, и вычислим значения
, производящие золотое сечение, и вычислим значения 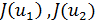 . Далее, если
. Далее, если 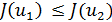 , то примем
, то примем 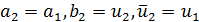 ;если же
;если же 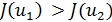 ., то примем
., то примем 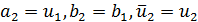 . Поскольку функция
. Поскольку функция 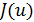 унимодальна на
унимодальна на 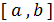 , то отрезок
, то отрезок 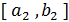 имеет хотя бы одну общую точку с множеством
имеет хотя бы одну общую точку с множеством 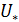 точек минимума
точек минимума 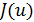 на
на 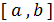 . Кроме того,
. Кроме того, 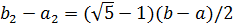 и весьма важно то, что внутри
и весьма важно то, что внутри 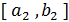 содержится точка
содержится точка 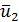 с вычисленным значением
с вычисленным значением 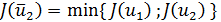 , которая производит золотое сечение отрезка
, которая производит золотое сечение отрезка 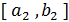 .
.
Пусть уже определены точки 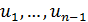 , вычислены значения
, вычислены значения 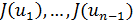 , найден отрезок
, найден отрезок 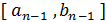 такой, что
такой, что 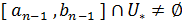 ,
, 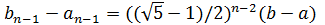 и известна точка
и известна точка 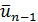 , производящая золотое сечение отрезка
, производящая золотое сечение отрезка 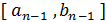 и такая, что
и такая, что 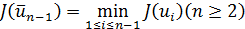 . Тогда в качестве следующей точки возьмем точку
. Тогда в качестве следующей точки возьмем точку 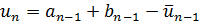 также производящую золотое сечение отрезка
также производящую золотое сечение отрезка 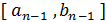 , вычислим значение
, вычислим значение 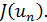
Пусть для определенности 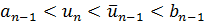 (случай
(случай 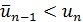 рассматривается аналогично). Если
рассматривается аналогично). Если 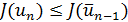 , то полагаем
, то полагаем 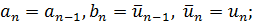 если же
если же 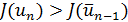 , то полагаем
, то полагаем 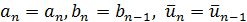 . Новый отрезок
. Новый отрезок 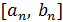 таков, что
таков, что 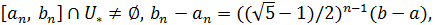 точка
точка 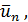 производит золотое сечение
производит золотое сечение 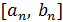 и
и 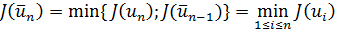 .
.
Если число вычислений значений J(u) заранее не ограничено, то описанный процесс можно продолжать, например, до тех пор, пока не выполнится неравенство 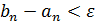 , где
, где 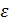 — заданная точность. Если же число вычислений значений функции
— заданная точность. Если же число вычислений значений функции 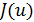 заранее жестко задано и равно п, то процесс на этом заканчивается и в качестве решения задачи второго типа можно принять пару
заранее жестко задано и равно п, то процесс на этом заканчивается и в качестве решения задачи второго типа можно принять пару 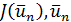 где
где 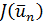 является приближением для +, а точка
является приближением для +, а точка 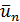 служит приближением для множества
служит приближением для множества 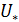 с погрешностью
с погрешностью 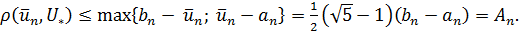
Вспомним, что с помощью метода деления отрезка пополам за 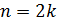 вычислений значений функции
вычислений значений функции 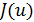 в аналогичном случае мы получили точку
в аналогичном случае мы получили точку 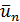 с погрешностью
с погрешностью 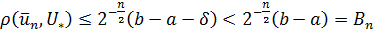
Отсюда имеем 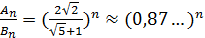 — видно, что уже при небольших
— видно, что уже при небольших 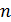 преимущество метода золотого сечения перед методом деления отрезка пополам становится ощутимым.
преимущество метода золотого сечения перед методом деления отрезка пополам становится ощутимым.
2. Обсудим возможности численной реализации метода золотого сечения на ЭВМ. Заметим, что число 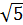 на ЭВМ неизбежно будет задаваться приближенно, поэтому первая точка
на ЭВМ неизбежно будет задаваться приближенно, поэтому первая точка 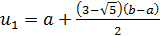 будет найдена с некоторой погрешностью. Посмотрпм, как повлияет эта погрешность на результаты последующих шагов метода золотого сечения. Обозначим
будет найдена с некоторой погрешностью. Посмотрпм, как повлияет эта погрешность на результаты последующих шагов метода золотого сечения. Обозначим 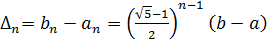
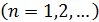 . Нетрудно проверить, что
. Нетрудно проверить, что 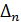 является решением конечно-разностного уравнения
является решением конечно-разностного уравнения 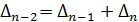 , или
, или 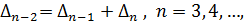 (1) с начальными условиями
(1) с начальными условиями 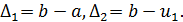
 Как известно
Как известно 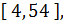 линейно независимые частные решения этого уравнения имеют вид
линейно независимые частные решения этого уравнения имеют вид 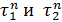 и (п = 1, 2,...), где
и (п = 1, 2,...), где 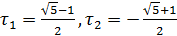 — корни характеристического уравнения
— корни характеристического уравнения 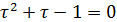 , а любое решение уравнения (1) представимо в виде
, а любое решение уравнения (1) представимо в виде 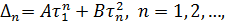 (2) где постоянные A и B однозначно определяются начальными условиями из линейной системы
(2) где постоянные A и B однозначно определяются начальными условиями из линейной системы 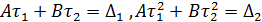 . (3)
. (3)
При 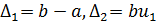 из (3) имеем
из (3) имеем 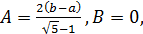 и понятно, что формула (2) в этом случае дает уже известное нам решение
и понятно, что формула (2) в этом случае дает уже известное нам решение 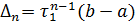 . Однако точка
. Однако точка 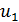 задана с погрешностью, поэтому в системе (3) вместо точного значения
задана с погрешностью, поэтому в системе (3) вместо точного значения 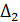 придется взять приближенное
придется взять приближенное 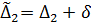 . Тогда постоянные A, B из (3) определятся с соответствующими погрешностями:
. Тогда постоянные A, B из (3) определятся с соответствующими погрешностями: 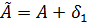 ,
, 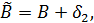 и вместо (2) с точными A, B будем иметь
и вместо (2) с точными A, B будем иметь 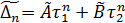 (п = 1, 2,...). Поскольку
(п = 1, 2,...). Поскольку 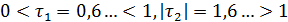 , то погрешность
, то погрешность 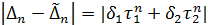 с возрастанием
с возрастанием 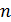 будет расти очень быстро. Это значит, что уже при не очень больших
будет расти очень быстро. Это значит, что уже при не очень больших 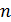 отрезок
отрезок 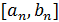 и точки
и точки 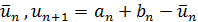 будут сильно отличаться от тех, которые получились бы при работе с точными данными. Численные эксперименты на ЭВМ также подтверждают, что метод золотого сечения в описанном выше виде практически неприменим уже при небольших
будут сильно отличаться от тех, которые получились бы при работе с точными данными. Численные эксперименты на ЭВМ также подтверждают, что метод золотого сечения в описанном выше виде практически неприменим уже при небольших 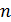 .
.
Как же быть? К счастью, имеется достаточно простая модификация метода золотого сечения, позволяющая избежать слишком быстрого возрастания погрешностей при определении точек 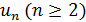 . А именно, на каждом отрезке
. А именно, на каждом отрезке 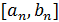 , содержащем точку
, содержащем точку 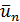 с предыдущего шага, при выборе следующей точки
с предыдущего шага, при выборе следующей точки 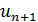 нужно остерегаться пользоваться формулой
нужно остерегаться пользоваться формулой 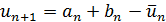 , и вместо этого лучше непосредственно произвести золотое сечение отрезка
, и вместо этого лучше непосредственно произвести золотое сечение отрезка 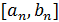 и в качестве
и в качестве 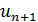 взять ту из точек
взять ту из точек 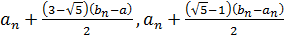 , которая наиболее удалена от
, которая наиболее удалена от 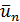 (здесь под
(здесь под 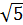 подразумевается какое-либо подходящее приближение этого числа). Конечно, после такой модификации метод золотого сечения, вообще говоря, теряет свойство симметричности и, быть может, уже не так красив, но зато вполне годится для приложений. Нетрудно видеть, что этот метод может применяться и без априорного знания о том, что минимизируемая функция унимодальна, но в этом случае полученное решение может оказаться далеким от глобального минимума.
подразумевается какое-либо подходящее приближение этого числа). Конечно, после такой модификации метод золотого сечения, вообще говоря, теряет свойство симметричности и, быть может, уже не так красив, но зато вполне годится для приложений. Нетрудно видеть, что этот метод может применяться и без априорного знания о том, что минимизируемая функция унимодальна, но в этом случае полученное решение может оказаться далеким от глобального минимума.
3. Метод золотого сечения относится к классу так называемых сим- метричных методов. Дадим краткое описание произвольного симметричного метода минимизации функции 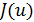 на отрезке
на отрезке 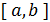 .
.
Первый шаг: на 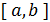 задается точка
задается точка 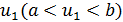 , полагается
, полагается 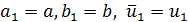 и вычисляется
и вычисляется 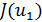 . Пусть уже сделано
. Пусть уже сделано 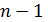 шагов
шагов 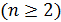 и найдены отрезок
и найдены отрезок 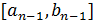 и точка
и точка 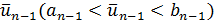 с вычисленным значением
с вычисленным значением 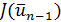 , причем
, причем 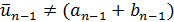 . Тогда на следующем n-м шаге берется точка
. Тогда на следующем n-м шаге берется точка 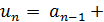
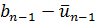 расположенная внутри [
расположенная внутри [ 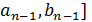 , симметрично точке
, симметрично точке 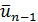 относительно середины этого отрезка — отсюда происходит название методов. Затем вычисляется значение
относительно середины этого отрезка — отсюда происходит название методов. Затем вычисляется значение 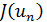 и сравнивается с
и сравнивается с 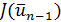 . Пусть для определенности
. Пусть для определенности 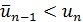 (случай
(случай 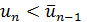 рассматривается аналогично). Тогда при
рассматривается аналогично). Тогда при 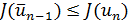 полагается
полагается 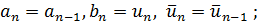 если же
если же 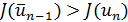 , то
, то 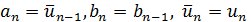 . Если
. Если 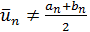 , то процесс может быть продолжен дальше. Может оказаться, что
, то процесс может быть продолжен дальше. Может оказаться, что 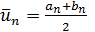 ,— в этом случае процесс заканчивается; при необходимости на
,— в этом случае процесс заканчивается; при необходимости на 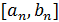 можно продолжать поиск минимума аналогичным методом, начиная с выбора новой начальной точки
можно продолжать поиск минимума аналогичным методом, начиная с выбора новой начальной точки 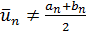 .
.
Из описания симметричного метода видно, что всякий симметричный метод полностью определяется заданием отрезка 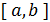 и первой точки
и первой точки 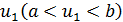 . Отсюда следует, что в качестве другой характеристики симметричного метода можно взять длины
. Отсюда следует, что в качестве другой характеристики симметричного метода можно взять длины 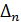 отрезков
отрезков 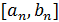 (п = 1, 2,...), где
(п = 1, 2,...), где 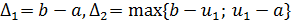 . Очевидно,
. Очевидно, 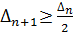 при всех
при всех 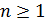 . Как видим, симметричные методы весьма просты и, пожалуй, даже изящны. Однако все эти методы страдают тем же недостатком, что и метод золотого сечения: погрешность, допущенная в задании первой точки
. Как видим, симметричные методы весьма просты и, пожалуй, даже изящны. Однако все эти методы страдают тем же недостатком, что и метод золотого сечения: погрешность, допущенная в задании первой точки 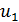 приводит к быстрому накапливанию погрешностей на дальнейших шагах, и уже при не очень больших п результаты будут сильно отличаться от тех, которые могли бы получиться при точной реализации симметричного метода с точными исходными данными.
приводит к быстрому накапливанию погрешностей на дальнейших шагах, и уже при не очень больших п результаты будут сильно отличаться от тех, которые могли бы получиться при точной реализации симметричного метода с точными исходными данными.
Если симметричный метод таков, что для 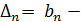
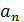 выполнено условие
выполнено условие
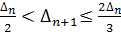 ,
, 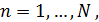 (4)
(4)
при некотором N > 1, то 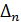 будут удовлетворять конечно-разностному уравнению (1) при
будут удовлетворять конечно-разностному уравнению (1) при 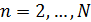 , и исследование поведения погрешностей в этом случае может быть проведено так же, как это было сделано выше для метода золотого сечения. Чтобы избежать слишком быстрого роста погрешностей в симметричных методах со свойством (4), на каждом отрезке
, и исследование поведения погрешностей в этом случае может быть проведено так же, как это было сделано выше для метода золотого сечения. Чтобы избежать слишком быстрого роста погрешностей в симметричных методах со свойством (4), на каждом отрезке 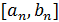 (
(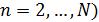 , содержащем точку
, содержащем точку 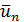 с предыдущего шага, следующую точку
с предыдущего шага, следующую точку 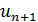 нужно определять не по формуле
нужно определять не по формуле 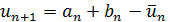 , а лучше принять за
, а лучше принять за 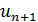 ту из точек
ту из точек 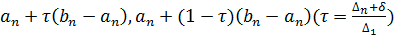 , которая наиболее удалена от
, которая наиболее удалена от