МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Математический факультет
Кафедра прикладной математики
ДИПЛОМНЫЙ ПРОЕКТ
сингулярное разложение в линейной задаче метода наименьших квадратов
Заведующий кафедрой прикладной
математики
Исполнил:
Научный руководитель
Владикавказ 2002
СОДЕРЖАНИЕ
ВВЕДЕНИЕ............................................................................................................................................................................. 3
Глава 1. Метод наименьших квадратов.................................................................................................. 7
1.1. Задача наименьших квадратов......................................................................................................... 7
1.2. Ортогональное вращение Гивенса................................................................................................... 9
1.3. Ортогональное преобразование Хаусхолдера......................................................................... 10
1.4. Сингулярное разложение матриц................................................................................................... 11
1.5. QR–разложение........................................................................................................................................ 15
1.6. Число обусловленности...................................................................................................................... 20
глава 2. Реализация сингулярного разложения.......................................................................... 25
2.1. Алгоритмы................................................................................................................................................. 25
2.2. Реализация разложения...................................................................................................................... 27
2.3. Пример сингулярного разложения.................................................................................................. 29
глава 3. Использование сингулярного разложения в методе наименьших квадратов.............................................................................................................................................................................. 33
ЗАКЛЮЧЕНИЕ................................................................................................................................................................... 38
ЛИТЕРАТУРА..................................................................................................................................................................... 39
ПРИЛОЖЕНИЕ 1. Исходные тексты программы............................................................................... 40
ПРИЛОЖЕНИЕ 2. контрольный пример..................................................................................................... 45
ВВЕДЕНИЕ
Метод наименьших квадратов обычно используется как составная часть некоторой более общей проблемы. Например, при необходимости проведения аппроксимации наиболее часто употребляется именно метод наименьших квадратов. На этом подходе основаны: регрессионный анализ в статистике, оценивание параметров в технике и т.д.
Большое количество реальных задач сводится к линейной задаче наименьших квадратов, которую можно сформулировать следующим образом.
Пусть даны действительная m ´ n –матрица A ранга k£min(m,n) и действительный m –вектор b. Найти действительный n –вектор x 0, минимизирующий евклидову длину вектора невязки Ax–b.
Пусть y – n– мерный вектор фактических значений, x – n– мерныйвектор значений независимой переменной, b – коэффициенты в аппроксимации y линейной комбинацией n заданных базисных функций j:
.
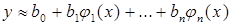Задача состоит в том, чтобы в уравнении подобрать такие b, чтобы минимизировать суммы квадратов отклонений e=y–Xb, где X – есть так называемая матрица плана, в которой строками являются n– мерный вектора с компонентами, зависящими от xj: 
каждая строка соответствует определенному значению xj. Коэффициенты можно найти решая нормальные уравнения 
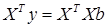, откуда 
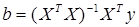. Покажем это. Возведем в квадрат выражение для е:
т. к. 
.
Это выражение имеет экстремум в точке, где 
=0
Откуда и получаем .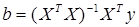
Следует отметить, что последнее выражение имеет в определенной степени формальный характер, т. к. решение нормальных уравнений, как правило, проводится без вычисления обратной матрицы (метод Крамера) такими методами как метод Гаусса, Холесского и т. д.
Пример. Пусть заданы результаты четырех измерений (рис. 1): y= 0при x= 0; y= 1 при x= 1; y= 2при x= 3; y= 5при x= 4. Задача заключается в том, чтобы провести через эти точки прямую 
таким образом, чтобы сумма квадратов отклонений была минимальна. Запишем уравнение, описывающее проведение прямой по результатам измерений. Мы получаем переопределенную систему:
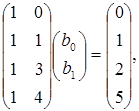
или Xb=y. Нам понадобится матрица XTX и обратная к ней:
Тогда решение b=(XTX)-1 XTy по методу наименьших квадратов будет иметь вид 
Таким образом, оптимальная прямая задается уравнением 
Метод точечной квадратичной аппроксимации (метод наименьших квадратов) не предполагает, что мы должны приближать экспериментальные данные лишь с помощью прямых линий. Во многих экспериментах связи могут быть нелинейными, и было бы глупо искать для этих задач линейные соотношения. Пусть, например, мы работаем с радиоактивным материалом. Тогда выходными данными у являются показания счетчика Гейгера в различные моменты времени t. Пусть наш материал представляет собой смесь двух радиоактивных веществ, и мы знаем период полураспада каждого из них, но не знаем, в каких пропорциях эти вещества смешаны. Если обозначить их количества через С и D, то показания счетчика будут вести себя подобно сумме двух экспонент, а не как прямая:
. (1)
На практике, поскольку радиоактивность измеряется дискретно и через различные промежутки времени, показания счетчика не будут точно
Рис. 1. Аппроксимация прямой линией.
соответствовать (1). Вместо этого мы имеем серию показаний счетчика 
в различные моменты времени 
, и (1) выполняется лишь приближенно:
Если мы имеем более двух показаний, m> 2, то точно разрешить эту систему относительно C и D практически невозможно. Но мы в состоянии получить приближенное решение в смысле минимальных квадратов.
Ситуация будет совершенно иной, если нам известны количества веществ C и D и нужно отыскать коэффициенты l и m. Это нелинейная задача наименьших квадратов, и решить ее существенно труднее. Мы по–прежнему будем минимизировать сумму квадратов ошибок, но сейчас она уже не будет многочленом второй степени относительно l и m, так что приравнивание нулю производной не будет давать линейных уравнений для отыскания оптимальных решений.
Глава 1. Метод наименьших квадратов