Или биномиальный закон распределения вероятностей. Исходя из моих наблюдений и личной статистики – это наиболее распространённый вид дискретного распределения, с которым мы уже встречались добрый десяток раз.
Я буду формулировать задачу в общем виде и попутно приводить конкретный пример:
Пусть проводится 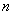 независимых испытаний (не обязательно повторных), в каждом из которых случайное событие
независимых испытаний (не обязательно повторных), в каждом из которых случайное событие 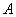 может появиться с вероятностью
может появиться с вероятностью 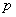 . Тогда случайная величина
. Тогда случайная величина 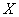 – число появлений события
– число появлений события 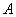 в данной серии испытаний, имеет биномиальное распределение.
в данной серии испытаний, имеет биномиальное распределение.
Совершенно понятно, что эта случайная величина может принять одно из следующих значений: 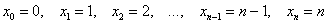 .
.
Например: монета подбрасывается 5 раз. Тогда случайная величина 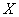 – количество появлений орла распределена по биномиальному закону. Орёл обязательно выпадет:
– количество появлений орла распределена по биномиальному закону. Орёл обязательно выпадет:
или 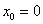 раз, или
раз, или 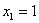 , или
, или 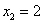 , или
, или 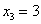 , или
, или 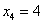 , или
, или 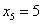 раз.
раз.
Как вы догадались, соответствующие вероятности определяются формулой Бернулли:
 , где:
, где:
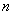 – количество независимых испытаний;
– количество независимых испытаний;
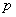 – вероятность появления события
– вероятность появления события 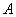 в каждом испытании;
в каждом испытании;
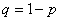 – вероятность непоявления события
– вероятность непоявления события 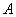 в каждом испытании;
в каждом испытании;
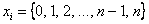 – сколько раз может появиться событие
– сколько раз может появиться событие 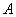 в данной серии испытаний (список всех возможных значений).
в данной серии испытаний (список всех возможных значений).
Сведём этот закон распределения в таблицу:
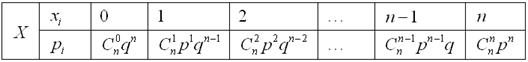
Вероятности 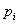 представляют собой члены бинома Ньютона, благодаря чему распределение и получило своё название. По формуле бинома:
представляют собой члены бинома Ньютона, благодаря чему распределение и получило своё название. По формуле бинома:
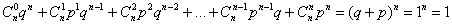 , что мы и ожидали увидеть.
, что мы и ожидали увидеть.
В нашем примере с монеткой:
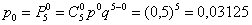 – вероятность того, что в 5 испытаниях орёл не выпадет вообще (
– вероятность того, что в 5 испытаниях орёл не выпадет вообще (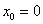 );
);
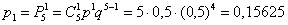 – вероятность того, что в 5 испытаниях орёл выпадет ровно
– вероятность того, что в 5 испытаниях орёл выпадет ровно 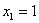 раз;
раз;
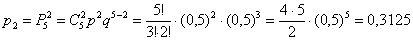 – вероятность того, что в 5 испытаниях орёл выпадет ровно
– вероятность того, что в 5 испытаниях орёл выпадет ровно 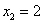 раза;
раза;
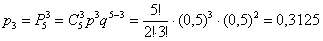 – … ровно
– … ровно 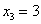 раза;
раза;
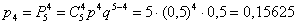 – … ровно
– … ровно 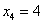 раза;
раза;
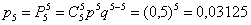 – … ровно
– … ровно 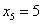 раз.
раз.
Таким образом, закон распределения числа выпавших орлов:

Контроль: 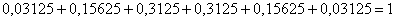
Легко видеть, что нахождение биномиального ряда распределения – есть занятие муторное, и это хорошо, если он содержит 3-4-5-6 значений. А ведь немало задач, где требуется рассчитать 8-10, а то и бОльшее количество вероятностей!
Поэтому вычисления целесообразно автоматизировать в Экселе с помощью его стандартной функции:
=БИНОМРАСП(m; n; p; 0), где 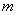 количество успехов в
количество успехов в 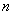 испытаниях, а
испытаниях, а 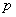 – вероятность успеха в каждом испытании.
– вероятность успеха в каждом испытании.
Именно так реализован Пункт 3 моего расчётного макета по ТерВеру, ну и особо крутая плюшка – это Пункт 6, в котором биномиальное распределение получается автоматически!
Однако на практике решение нужно расписывать подробно, да и техника не всегда бывает под рукой. В этой связи обязательно прорешайте хотя бы 2-3 типовых задачи и постукайте пальцами по клавишам микрокалькулятора.
Начинаем:
Задача
Вероятность поражения цели при одном выстреле равна 0,6. Составить закон распределения случайной величины 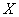 – числа попаданий в цель при четырех выстрелах. Вычислить
– числа попаданий в цель при четырех выстрелах. Вычислить 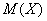 и
и 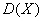 . Построить многоугольник и функцию распределения. Найти
. Построить многоугольник и функцию распределения. Найти 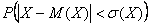 .
.
…таких задач очень много – составить закон распределения вероятностей и найти всё-всё-всё. Или почти всё. Или что-то ещё – зависит от фантазии составителя:)
Решение: по существу, текст условия совпадает с Задачей статьи о геометрическом распределении, но есть одно принципиальное отличие – здесь другая случайная величина. А именно, под страхом расстрела совершается серия из 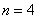 и строго из 4 выстрелов, вероятность попадания в каждом из которых составляет
и строго из 4 выстрелов, вероятность попадания в каждом из которых составляет 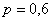 .
.
Очевидно, что испытания независимы, и случайная величина 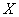 распределена по биномиальному закону.
распределена по биномиальному закону.
Составим ряд распределения данной случайной величины. Используем формулу Бернулли:
 для
для 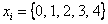 – всех возможных результатов рассматриваемой серии.
– всех возможных результатов рассматриваемой серии.
На этом шаге я сразу забью 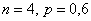 в свой расчётный макет (Пункт 6), чтобы контролировать правильность каждого пункта. Для удобства их можно нумеровать:
в свой расчётный макет (Пункт 6), чтобы контролировать правильность каждого пункта. Для удобства их можно нумеровать:
0) 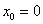
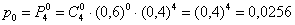 – вероятность того, что в 4 выстрелах не будет попаданий;
– вероятность того, что в 4 выстрелах не будет попаданий;
1) 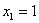
 – вероятность того, что в 4 выстрелах будет ровно 1 попадание;
– вероятность того, что в 4 выстрелах будет ровно 1 попадание;
2) 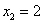
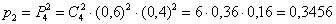 – … ровно 2 попадания;
– … ровно 2 попадания;
3) 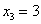
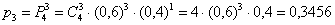 – … ровно 3 попадания;
– … ровно 3 попадания;
4) 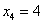
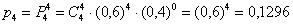 – … ровно 4 попадания.
– … ровно 4 попадания.
Таким образом, искомый закон распределения:

Проверка: 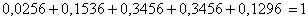 ,ч.т.п.
,ч.т.п.
Пока таблица не ушла из поля зрения, построим многоугольник распределения:
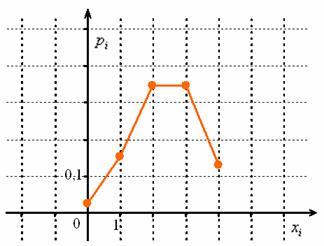
Вычислим математическое ожидание и дисперсию. И тут есть отличная новость – для биномиального распределения можно не использовать общий алгоритм расчёта этих числовых характеристик – по той причине, что существуют готовые формулы:
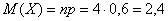 – среднеожидаемое количество попаданий;
– среднеожидаемое количество попаданий;
 – рассеяние количества попаданий относительно матожидания.
– рассеяние количества попаданий относительно матожидания.
Всегда бы так!
Составим функцию распределения вероятностей:
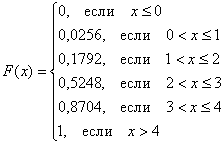
Я не буду вновь останавливаться на алгоритме её построения, и если что-то не понятно, то смотрите по ссылке выше. Раз ступенька, два ступенька – будет график:
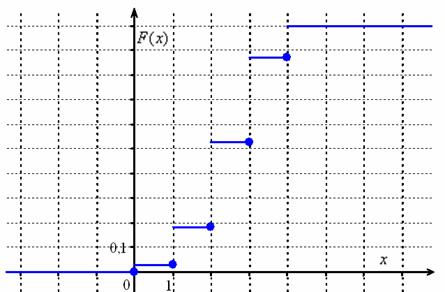
Напоминаю, что в статье о функции распределения можно разыскать программу, которая строит чертежи автоматически.
Найдём 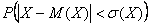 – вероятность того, что значение случайной величины
– вероятность того, что значение случайной величины 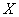 отклонится от своего математического ожидания не более чем на одно среднее квадратическое отклонение.
отклонится от своего математического ожидания не более чем на одно среднее квадратическое отклонение.
Среднее квадратическое отклонение: 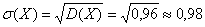
и искомая вероятность:
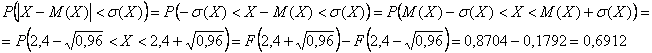
(в чём смысл этого пункта решения?)
Готово.
Как вариант, в разобранной задаче может быть предложена другая случайная величина: не количество попаданий, а 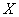 – количество промахов. Нетрудно догадаться, что в этом случае вероятности «развернутся наоборот»
– количество промахов. Нетрудно догадаться, что в этом случае вероятности «развернутся наоборот» 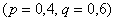 , и числовые характеристики с графиками будут другими.
, и числовые характеристики с графиками будут другими.
БУДЬТЕ ВНИМАТЕЛЬНЫ!
Дополнительные и многочисленные задания по теме можно найти в pdf-сборнике, и как я рекомендовал выше – непременно прорешайте пару-тройку задач вручную! Как говорится, автопилот хорошо, но без ручного управления – финиш.
На очереди распределение Пуассона и гипергеометрическое распределение вероятностей.