ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Перпендикулярные прямые в пространстве
Теорема
Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они перпендикулярны.
Доказательство
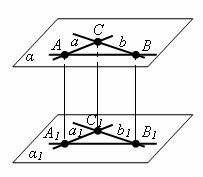
Пусть a и b – перпендикулярные прямые, a1 и b1 – параллельные им пересекающиеся прямые.
Если прямые a, b, a1, b1 лежат в одной плоскости, то они обладают указанными в теореме свойством, кА это известно из планиметрии.
Предположим, что прямые е лежат в одной плоскости. Тогда прямые a и b лежат в плоскости α, а прямые a1 и b1 – в некоторой плоскости α1. По теореме о признаке параллельных прямых плоскости α и α1 параллельны. Пусть С – точка пересечения прямых a и b, а точка С – точка пересечения прямых a1 и b1. Проведем в плоскости параллельных прямых a и a1 прямую, параллельную прямой СС1. Она пересечет прямые a и a1 в точках A и A1. В плоскости прямых b и b1 проведем прямую, параллельную прямой СС1, и обозначим через B и B1 точки ее пересечения с прямыми b и b1.
Четырехугольник CAA1C1 и CBB1C1 – параллелограммы, так как у них противолежащие стороны параллельны. Четырехугольник ABB1A1 так же параллелограмм. У него стороны AA1, BB1 параллельны, потому что каждая из них параллельна прямой CC1. Следовательно, четырехугольник лежит в плоскости, проходящей через параллельные прямые AA1 и BB1. Эта плоскость пересекает параллельные плоскости α и α1 по параллельным прямым AB и A1B1.
Так как у параллелограмма противолежащие стороны равны, то AB = A1B1, AC = A1C1, BC = B1C1. Δ ABC = ΔA1B1C1 (по третьему признаку равенства треугольников). ∠ ACB = ∠A1C1B1 = 90º. Следовательно, прямые a1 и b1 перпендикулярны. Теорема доказана.
Признак перпендикулярности прямой и плоскости
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
Теорема
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной прямой.
Доказательство
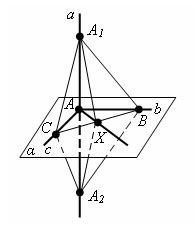
Пусть a – прямая, перпендикулярная прямым b и с в плоскости α. Тогда прямая a проходит через точку A пересечения прямых b и с. Докажем, что прямая a перпендикулярна плоскости α.
Проведем произвольную прямую x через точку A в плоскости α и покажем, что она перпендикулярна прямой a. Проведем в плоскости α произвольную прямую, не проходящую через точку A и пересекающую прямые b, с и x. Пусть точками пересечения будут B, C и X..
Отложим на прямой a от точки A в разные стороны равные отрезки AA1 и AA2. Треугольник A1CA2 равнобедренный, так как отрезок AC является высотой по условию теоремы и медианой по построению. Треугольник A1BA2 так же равнобедренный. Следовательно, Δ A1BC = ΔA2BC по третьему признаку равенства треугольников.
Из равенства треугольников A1BC и A2BC следует равенство углов A1BX и A2BX, следовательно, равенство треугольников A1BX и A2BX по первому признаку равенства треугольников. Из равенства сторон A1X и A2X, следует, что A1XA2 равнобедренный. Поэтому его медиана XA является высотой. А это и значит, что прямая x перпендикулярна a. По определению прямая a перпендикулярна плоскости α. Теорема доказана.
Свойство перпендикулярной прямой и плоскости
Теорема
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Доказательство
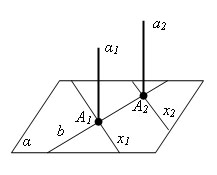
Пусть a1 и a2 – две параллельные прямые и α - плоскость, перпендикулярная прямой a1. Докажем, что эта плоскость перпендикулярна и прямой a2.
Проведем через точку A2 пересечения прямой a2 с плоскостью α произвольную прямую x2 в плоскости α. Проведем в плоскости α через точку A1 пересечения прямой a1 и α прямую x1, параллельную прямой x2. Так как прямая a1 перпендикулярна плоскости α, то прямые a1 и x1 перпендикулярны. По теореме о перпендикулярности прямых в пространстве параллельные им пересекающиеся прямые a2 и x2 тоже перпендикулярны. Таким образом, прямая a2 перпендикулярна любой прямой x2 в плоскости α. A это значит, что прямая a2 перпендикулярна плоскости α. Теорема доказана.
Свойство прямых перпендикулярных плоскости
Теорема
Две прямые, перпендикулярные одной и той же плоскости, параллельны.

Доказательство
Пусть a и b – две прямые, перпендикулярные плоскости α.
Предположим, что прямые a и b не параллельны.
Выберем на прямой b точку С, не лежащую в плоскости α. Проведем через точку С прямую b`, параллельную прямой a. Прямая b` перпендикулярна плоскости α. Пусть B и B` - точки пересечения прямых b и b` с плоскостью α. Тогда прямая BB` перпендикулярна пересекающимся прямым b и b`. А это невозможно и противоречит предположению. Теорема доказана.
Перпендикуляр и наклонная
Перпендикуляром, опущенным из данной точки данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
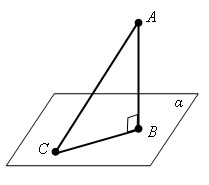
AB – перпендикуляр к плоскости α.
AC – наклонная, CB – проекция.
С – основание наклонной, B - основание перпендикуляра.