Цели: Ввести понятия эквиполлентного отрезка, вектора; установить связь между понятиями «вектор» и «эквиполлентный отрезок»; расмотреть действия над векторами и их свойства; ввести понятия базиса плоскости, базиса пространства; сформулировать и доказать теоремы о разложении вектора по базису на плоскости и в пространстве; систематизировать и обобщить и знания студентов по теме «Векторы на плоскости и в пространстве».
План лекции.
1. Эквиполлентные отрезки и основные теоремы о них.
2. Понятие вектора.
3. Виды векторов.
4. Действия над векторами и их свойства (геометрическая интерпритация, в координатах).
5. Теорема об откладывании вектора от произвольной точки плоскости (пространства).
6. Теоремы о разложении вектора по базису на плоскости (в пространстве).
7. Линейная зависимость векторов.
Примерное содержание лекции.
 Определение 1.1 Отрезок АВ, у которого указан порядок концов, называется направленным отрезком: точка А называется «началом», а точка «В» - «концом» направленного отрезка АВ.
Определение 1.1 Отрезок АВ, у которого указан порядок концов, называется направленным отрезком: точка А называется «началом», а точка «В» - «концом» направленного отрезка АВ.
Направленный отрезок АВ обозначается 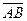
Длину направленного отрезка 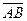 обозначают
обозначают  .
.
Определение 1.2. Нулевым направленным отрезком называется отрезок, у которого начало и конец совпадают.
Определение 1.3. Ненулевые отрезки 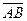 и
и  называются эквиполлентными, если их направления совпадают, и они имеют равные длины.
называются эквиполлентными, если их направления совпадают, и они имеют равные длины.
Обозначается: 
 Определение 1.4. Направленные отрезки
Определение 1.4. Направленные отрезки 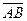 и
и  называются сонаправленными (противоположно направленными), если они имеют одинаковое (противоположное) направление.
называются сонаправленными (противоположно направленными), если они имеют одинаковое (противоположное) направление.


 ,
,  =
= 
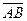

 ,
, 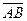


Теорема 1.5. (признак эквиполлентности) Два отрезка  и
и  эквиполлентны тогда и только тогда, когда середины отрезков
эквиполлентны тогда и только тогда, когда середины отрезков  и
и  совпадают.
совпадают.
 а) б)
а) б)
 |
Отношение эквиполлентности является отношением эквивалентности:
1)  (рефлексивность);
(рефлексивность);
2) 

 (симметричность);
(симметричность);
3)  ,
, 

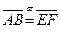 (транзитивность).
(транзитивность).
Определение 1.6. Вектором называется класс эквиполлентных отрезков.
Обозначаются:  или
или 
Определение 1.7. Длиной или модулем ненулевого вектора  называется длина направленного отрезка
называется длина направленного отрезка 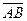 .
.
Обозначается: 
Определение 1.8. Вектор, длина которого равна единице, называется единичным вектором.
Определение 1.9. Векторы  и
и  называются одинаково направленными (сонаправленными) (обозначают
называются одинаково направленными (сонаправленными) (обозначают  ), если одинаково направлены изображающие их направленные отрезки, и противоположно направленными (обозначают
), если одинаково направлены изображающие их направленные отрезки, и противоположно направленными (обозначают  ), если противоположно направлены изображающие их отрезки.
), если противоположно направлены изображающие их отрезки.
Определение 1.10. Векторы  и
и  называются коллинеарными, если существует прямая, которой они параллельны (два ненулевых вектора называются коллинеарными, если они сонаправлены или противоположно направлены).
называются коллинеарными, если существует прямая, которой они параллельны (два ненулевых вектора называются коллинеарными, если они сонаправлены или противоположно направлены).
Нулевой вектор коллинеарен любому вектору.
Определение 1.11. Два вектора называются равными, если они сонаправлены и имеют одинаковую длину (обозначают 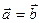 ).
).
Определение 1.12. Векторы  и
и  называются противоположными, если они имеют равные длины и противоположные направления.
называются противоположными, если они имеют равные длины и противоположные направления.
Вектор, противоположный вектору  , обозначают
, обозначают 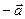
Лемма 1.13. (о равенстве векторов) Если  , то
, то  .
.
 Доказательство:
Доказательство:
1. 

 по признаку эквиполлентности следует, что середины отрезков
по признаку эквиполлентности следует, что середины отрезков  и
и  совпадают.
совпадают.
2. 


Теорема 1.14. Пусть  - произвольный вектор плоскости, точка О- произвольная точка плоскости. Тогда существует одна и только одна точка М, такая что
- произвольный вектор плоскости, точка О- произвольная точка плоскости. Тогда существует одна и только одна точка М, такая что  .
.
 Доказательство:
Доказательство:
1) Докажем существование такой точки  , что
, что  .
.
а) Допустим, что  ;
;
б) Рассмотрим середину отрезка ОВ – точку С. Построим точку М, симметричную точке А относительно точки С;
в) По признаку эквиполлентности 

2) Докажем единственность точки М.
а) Пусть точка М не единственна. Тогда существует точка  такая, что
такая, что 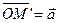 и
и  ;
;
б) По лемме о равенстве векторов имеем:  , т.е. точки М и М’ совпадают. Следовательно, точка М- единственная.
, т.е. точки М и М’ совпадают. Следовательно, точка М- единственная. 
Действия над векторами.
I. Сложение векторов
| Правило сложения векторов | Чертеж | Свойства сложения векторов | ||
1. Правило треугольника:
Если даны два вектора  и и  , то от произвольной точки А плоскости откладывают вектор , то от произвольной точки А плоскости откладывают вектор  , затем от точки В откладывают вектор , затем от точки В откладывают вектор  . Вектор . Вектор  , соединяющий начало вектора , соединяющий начало вектора  и конец вектора и конец вектора  , называется суммой векторов , называется суммой векторов  и и  . .
| 


| 1. Коммутативность:
Для любых векторов  и и  имеет место равенство: имеет место равенство:  2. Ассоциативность:
Для любых векторов
2. Ассоциативность:
Для любых векторов  и и 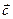 имеет место равенство: имеет место равенство:
 3. Свойство нуль-вектора:
Для любого вектора
3. Свойство нуль-вектора:
Для любого вектора  имеет место равенство: имеет место равенство:
 4. Существование и единственность противоположного вектора:
Для любого вектора
4. Существование и единственность противоположного вектора:
Для любого вектора  плоскости существует противоположный вектор плоскости существует противоположный вектор 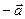 , и притом единственный, такой, что: , и притом единственный, такой, что:

| ||
2. Правило параллелограмма
Если даны два вектора  и и  , то от произвольной точки А плоскости откладывают векторы , то от произвольной точки А плоскости откладывают векторы  и и  , затем на отрезках , затем на отрезках  и и  строят параллелограмм, как на сторонах, выходящих из одной вершины. Вектор – диагональ строят параллелограмм, как на сторонах, выходящих из одной вершины. Вектор – диагональ  есть искомая сумма векторов есть искомая сумма векторов  и и 
| 


| |||
3. Правило многоугольника
Если даны векторы  , то от произвольной точки А откладываем последовательно векторы , то от произвольной точки А откладываем последовательно векторы  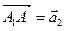 , ,  , ,  , …Применяя последовательно правило треугольника сначала для векторов , …Применяя последовательно правило треугольника сначала для векторов  , затем – для , затем – для 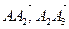 и т.д., находим сумму векторов и т.д., находим сумму векторов  - вектор, соединяющий начало вектора - вектор, соединяющий начало вектора  и конец вектора и конец вектора 
|
|
II. Вычитание векторов
 Определение 1.15. Разностью двух векторов
Определение 1.15. Разностью двух векторов  и
и  называется такой вектор
называется такой вектор  , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор  , т.е.
, т.е.  .
.
Пусть  , то
, то  , так как по правилу треугольника
, так как по правилу треугольника  .
.
Вычитание можно свести к сложению векторов. Действительно, если  , то
, то  . Получим:
. Получим:  .
.
Значит,  . Из данного соотношения следует, что из одной части векторного равенства в другую его часть можно переносить вектор, изменяя его знак на противоположный.
. Из данного соотношения следует, что из одной части векторного равенства в другую его часть можно переносить вектор, изменяя его знак на противоположный.
III. Умножение вектора на число
Определение 1.16. Произведением вектора  на число
на число  называется такой вектор
называется такой вектор  , который удовлетворяет условиям:
, который удовлетворяет условиям:
1. Длина вектора  равно произведению длины вектора
равно произведению длины вектора  и модуля числа
и модуля числа  , т.е.
, т.е.  ;
;
2. Вектор  сонаправлен с вектором
сонаправлен с вектором  , если
, если  ; противоположно направлен вектору
; противоположно направлен вектору  , если
, если  , то есть
, то есть  , если
, если  и
и  , если
, если  .
.
 |
Свойства умножения вектора на число:
1. Ассоциативность:
Для любых чисел  и любого вектора
и любого вектора  имеет место равенство:
имеет место равенство:  .
.
2. Дистрибутивность умножения относительно сложения чисел:
Для любых чисел  и любого вектора
и любого вектора  имеет место равенство:
имеет место равенство:  ;
;
3. Дистрибутивность умножения относительно сложения векторов:
Для любых векторов  и
и  и любого числа
и любого числа  имеет место равенство:
имеет место равенство:  .
.
4. Свойство нуль-вектора:
Если  или
или  , то
, то 
Теорема 1.17. Если два вектора  и
и  коллинеарны и вектор
коллинеарны и вектор  не является нулевым вектором, то существует единственный скаляр
не является нулевым вектором, то существует единственный скаляр  R такой, что
R такой, что  .
.
Доказательство:
I. Докажем, что  - существует.
- существует.
1. Из условия коллинеарности векторов следует, что  или
или  ;
;
2. В случае  положим, что
положим, что 
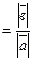 , в случае
, в случае  -
- 
 ;
;
3. По определению произведения вектора на число имеем равенство  .
.
II. Докажем, что  - единственный (метод от противного).
- единственный (метод от противного).
1. Пусть существует 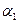
 R такое, что
R такое, что 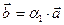 ;
;
2. По условию  ;
;
3. Так как вектор  определяется однозначно, то
определяется однозначно, то 




 (
(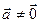 по условию)
по условию) 
 - единственно
- единственно
Два вектора  и
и  параллельны некоторой плоскости
параллельны некоторой плоскости  , если они параллельны некоторым прямым, лежащим в этой плоскости. Очевидно, если два вектора лежат в некоторой плоскости, то они параллельны и самой этой плоскости.
, если они параллельны некоторым прямым, лежащим в этой плоскости. Очевидно, если два вектора лежат в некоторой плоскости, то они параллельны и самой этой плоскости.
Определение 1.18. Векторы  ,
,  и
и  называются компланарными, если существует плоскость, которой они параллельны.
называются компланарными, если существует плоскость, которой они параллельны.
Если один из тройки векторов нулевой вектор, то эти векторы будут также компланарны.
Теорема 1.19. Если векторы  ,
,  и
и  - компланарны, а векторы
- компланарны, а векторы  и
и  не являются нулевыми векторами, то существуюттакие
не являются нулевыми векторами, то существуюттакие  и
и 
 R, причем единственные, что
R, причем единственные, что  .
.
Доказательство:
I. Докажем существование  и
и  .
.
1. Пусть  . Из условия компланарности векторов
. Из условия компланарности векторов  ,
,  и
и  принадлежатодной плоскости. По теореме 1.14. эти векторы можно отложить от некоторой точки О плоскости.
принадлежатодной плоскости. По теореме 1.14. эти векторы можно отложить от некоторой точки О плоскости.
Возможны 3 случая:
а) С 

 б) С
б) С 


 | |||
 | |||
в) С 
 ; С
; С 

o  Проведем из точки С прямые
Проведем из точки С прямые  | |
| |  и
и  | |
| |  ;
;
o По правилу треугольника имеем:
 =
=  ;
;
o 
o Значит:  =
= 
 +
+ 
 или
или  =
= 
 +
+ 
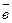 .
.
II. Докажем единственность  и
и  .
.
1. Пусть существует 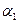 и
и 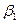 , такие что
, такие что 
2. По условию  ;
;
3. Так как вектор 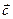 определяется однозначно, то
определяется однозначно, то 

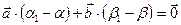
4. Равенство возможно, если  =
=  и
и 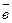 =
=  , но это противоречит условию.
, но это противоречит условию.
Следовательно, 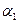 =
=  ,
, 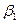 =
=  , т.е.
, т.е. 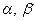 - единственны.
- единственны.
Таким образом, мы показали, что если на плоскости дана упорядоченная пара 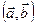 неколлинеарных векторов, для любого вектора
неколлинеарных векторов, для любого вектора  этой плоскости существует единственная упорядоченная пара чисел
этой плоскости существует единственная упорядоченная пара чисел  такая, что выполняется равенство
такая, что выполняется равенство  . Данное равенство называется разложением вектора
. Данное равенство называется разложением вектора 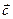 по двум неколлинеарным векторам
по двум неколлинеарным векторам  и
и  ; числа
; числа  и
и  называются коэффициентами разложения.
называются коэффициентами разложения.
Пару векторов 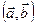 называют базисом на плоскости, а также на множестве всех векторов пространства, компланарных с векторами
называют базисом на плоскости, а также на множестве всех векторов пространства, компланарных с векторами  и
и  .
.
Равенство  называется разложением вектора
называется разложением вектора 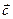 по базису
по базису 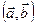
Определение 1.20. Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов. Векторы этой пары называются базисными векторами.
Принято базис на плоскости обозначать как 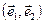 .
.
Определение 1.21. Коэффициенты в разложении вектора по базису называются координатами вектора.
Вектор 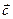 в базисе
в базисе 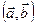 имеет координаты
имеет координаты  . В дальнейшем координаты любого вектора будем обозначать как
. В дальнейшем координаты любого вектора будем обозначать как 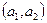 .
.
Принято считать, что базисные векторы имеют следующие координаты:  .
.
Свойства координат вектора 1.22 :
1.22.1. Каждая координата суммы двух векторов равна сумме соответствующих координат слагаемых векторов.
1.22.2 Каждая координата разности двух векторов равна разности соответственных координат этих векторов.
1.22.3. При умножении вектора на число каждая координата умножается на это число.
1.22.4. Координаты коллинеарных векторов пропорциональны.
Определение 1.23. Вектор  , где
, где  R, а векторы
R, а векторы 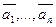 не являются нулевыми, называются линейной комбинацией векторов
не являются нулевыми, называются линейной комбинацией векторов 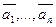 .
.
Иначе говоря, вектор 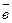 выражается через векторы
выражается через векторы 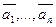 .
.
Определение 1.24. Система векторов 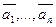 , называется линейно зависимой, если существуют числа
, называется линейно зависимой, если существуют числа  , такие, что хотя бы одно из них отлично от нуля и выполняется равенство
, такие, что хотя бы одно из них отлично от нуля и выполняется равенство 
Определение 1.25. Система векторов 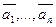 , называется линейно независимой, если равенство
, называется линейно независимой, если равенство  справедливо только при числах, равных нулю, т.е.
справедливо только при числах, равных нулю, т.е.  =
= 
Свойства системы линейно зависимых векторов 2.10.:
1.25.1. При n > 1 система векторов 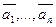 линейно зависима тогда и только тогда, когда хотя бы один из векторов является линейной комбинацией остальных векторов этой системы.
линейно зависима тогда и только тогда, когда хотя бы один из векторов является линейной комбинацией остальных векторов этой системы.
Доказательство:
1. Пусть система векторов линейно зависима, тогда выполняется равенство:
 (1)
(1)
2. Пусть  . Разделим обе части равенства (1) на
. Разделим обе части равенства (1) на  :
:

Таким образом,  является линейной комбинацией остальных векторов системы.
является линейной комбинацией остальных векторов системы.
3.Обратно, пусть в системе векторов 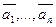 вектор
вектор  является линейной комбинацией остальных векторов
является линейной комбинацией остальных векторов  (3).
(3).
4. Равенство (3) можно записать так: 
Так как коэффициент перед вектором  равен (-1), то по определению 2.5 система векторов
равен (-1), то по определению 2.5 система векторов 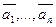 линейно зависима.
линейно зависима.
1.25.2. Если часть данной системы векторов является линейно-зависимой, то и вся система является линейно-зависимой.
1.25.3. Система линейно независимых векторов не содержит нулевого вектора.
1.25.4. Если система векторов линейно независима, то любая её часть также линейно независима.
Теорема 1.26. Система векторов  и
и 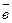 линейно - зависима тогда и только тогда, когда эти векторы коллинеарны.
линейно - зависима тогда и только тогда, когда эти векторы коллинеарны.
Доказательство:
I. Система векторов  и
и 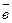 линейно – зависима. Доказать, что векторы
линейно – зависима. Доказать, что векторы  и
и 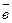 коллинеарны.
коллинеарны.
1. По определению 2.8  , где
, где  .
.
2. По свойству действий над векторами имеем:


 вектор
вектор  - линейная комбинация
- линейная комбинация  и по теореме
и по теореме
2.1  коллинеарен
коллинеарен  .
.
II. Пусть векторы  и
и  коллинеарны. Докажем, что система этих векторов линейно зависима.
коллинеарны. Докажем, что система этих векторов линейно зависима.
1. По теореме 2.1 имеем:  ;
;
2. По свойству действий над векторами:  . Значит, система векторов
. Значит, система векторов  и
и  линейно зависима по определению 2.10, т.к. один из коэффициентов отличен от нуля.
линейно зависима по определению 2.10, т.к. один из коэффициентов отличен от нуля.
Теорема 1.27. Система векторов  ,
,  и
и  линейно зависима тогда и только тогда, когда эти векторы компланарны.
линейно зависима тогда и только тогда, когда эти векторы компланарны.
Доказательство:
1. По определению линейно зависимой системы векторов имеем 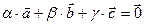 причем, хотя бы один из коэффициентов отличен от 0. Компланарность векторов очевидна.
причем, хотя бы один из коэффициентов отличен от 0. Компланарность векторов очевидна.
2. Пусть ни один из коэффициентов  ,
,  и
и 
 .
.
o  Отложим от некоторой точки О плоскости вектор
Отложим от некоторой точки О плоскости вектор  затем от точки А
затем от точки А  ;
;
o Так как  , то
, то  . С другой стороны
. С другой стороны 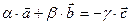 . Значит,
. Значит, 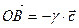 .
.
o Через точки О, А, В можно провести некоторую плоскость  . Так как
. Так как  , то из равенств
, то из равенств 
 ,
, 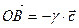 следует, что векторы
следует, что векторы 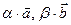 и
и  параллельны плоскости
параллельны плоскости  и поэтому они компланарны.
и поэтому они компланарны.
o Обратно, пусть векторы  ,
,  и
и  компланарны. Тогда по теореме 2.2. имеем, что
компланарны. Тогда по теореме 2.2. имеем, что  или
или  . Значит, система векторов
. Значит, система векторов  ,
,  и
и 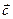 линейно зависима по определению 2.5, т.к. один из коэффициентов отличен от нуля.
линейно зависима по определению 2.5, т.к. один из коэффициентов отличен от нуля.


