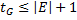Эволюция взвешенного орграфа

Определение 1. Ориентированным графом (орграфом) будем называть упорядоченную пару множеств 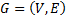. При этом 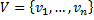(где 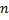– положительное целое число), а 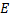– некоторое отношение, заданное над 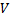(). Элементы 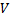и 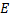будем соответственно называть вершинами и дугами 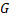. Чтобы показать, что 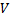и 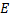являются множеством вершин и множеством дуг орграфа 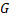будем писать 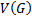и .

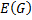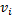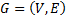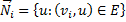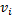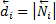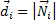Определение 2. Входящей и выходящей окрестностью вершины орграфа будем соответственно называть множества и . При этом входящей и выходящей степенью будем называть числа и . Вершины с нулевой входящей и выходящей степенью будем называть соответственно источником и стоком.

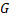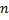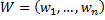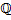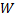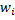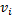Определение 3. Пусть – -вершинный орграф, и – вектор с элементами из . Пару будем называть взвешенным орграфом, – вектором весов, а () – весом вершины . Для удобства чтения, говоря о 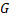, мы иногда будем иметь в виду , а, говоря о – 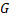(так, под вершинами будут пониматься вершины 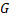). Общим весом орграфа с вектором весов будем называть число .

Определение 4. Каждый взвешенный орграф порождает бесконечную последовательность взвешенных орграфов 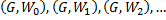, такую что

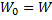
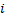-й элемент 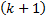-го вектора последовательности 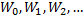определяется как:

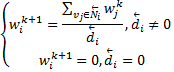
Данную последовательность будем называть эволюцией . Общий вес 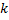-го графа эволюции будет обозначаться как .

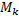Определение 5. Матрица входов 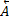орграфа 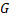получается заменой каждого элемента 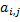в каждом ненулевом столбце 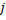матрицы смежности 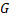на .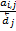

Теорема 1. Пусть 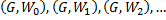– эволюция взвешенного орграфа с матрицей входов 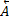. Тогда 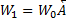(и, следовательно, ).

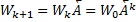Доказательство. Непосредственно следует из определений 4 и 5

Определение 6. Регулярным будем называть такой орграф, входящие и выходящие степени всех вершин которого равны одному и тому же числу 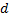, которое будем называть степенью орграфа.

Следствие 1. Пусть 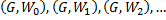– эволюция регулярного взвешенного орграфа, тогда 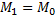(и, следовательно, ).

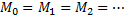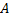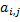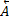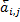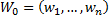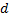Доказательство. Обозначим элементы матрицы смежности графа через , а элементы матрицы входов через . Пусть и – степень графа. По теоремe 1 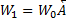, откуда, воспользовавшись определениями 4 и 5, получаем

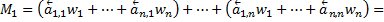
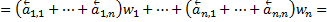
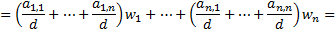
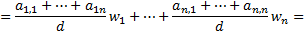
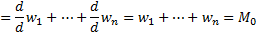
Теорема 2. Пусть 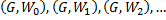– эволюция взвешенного орграфа, вершины которого имеют ненулевые входящие степени. Пусть также 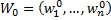, 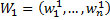. Тогда найдутся такие 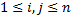, что , .

Доказательство. Выберем 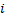и 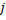такими, чтобы выполнялись условия 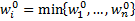и

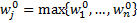
Определение 7. Пусть 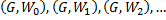– эволюция взвешенного орграфа 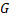. Если существует натуральное 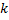, такое что , то будем говорить, что 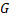стабилизируется. При этом наименьшее 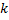, удовлетворяющее обозначенному условию, будет называться временем стабилизации, 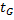. Если 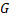не стабилизируется, будем писать .

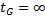Определение 8. Рассмотрим орграф 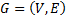. Последовательность его, быть может, повторяющихся вершин () будем называть маршрутом (длины 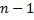), если для любых соседних вершин последовательност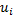и и 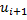выполнено условие 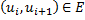. При 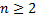будем обозначать данный маршрут как 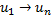, а при 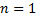будем говорит о тривиальном маршруте (длины 0). Маршруты, начинающиеся и заканчивающиеся одной и той же вершиной, будем называть контурами. Будем говорить, что 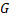бесконтурный, если нельзя указать последовательности вершин 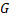, являющейся контуром. Маршрут, состоящий из попарно различных вершин, будем называть путём.

Лемма 1. В бесконтурном орграфе все вершины являются источниками или найдётся вершина с непустой входящей окрестностью, состоящей из источников.

Доказательство. Рассмотрим орграф , полагая, что не все его вершины являются источниками. Значит, подмножество 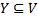вершин с непустой входящей окрестностью непусто. Пусть , т.е. 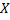– множество источников. Положим, что не существует такой вершины 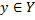, чья входящая окрестность является подмножеством 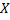. Тогда все вершины орграфа 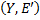, где 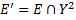, имеют ненулевые входящие степени. Рассматривая в данном графе путь максимальной длины, видим, что существует такая дуга 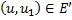, что 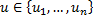. Это даёт контур 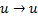, тогда как граф 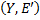должен быть бесконтурным. Полученное противоречие доказывает существование требуемой вершины 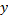с непустой окрестностью, состоящей из источников

Теорема 3. Пусть 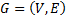– бесконтурный взвешенный орграф, тогда .

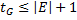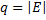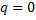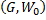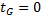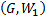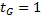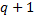Доказательство. Докажем утверждение индукцией по . Истинность базового случая следует непосредственно из определения 4: если вершины имеют нулевые веса, то ; в противном случае нулевые веса имеют вершины , откуда . Положим теперь, что утверждение верно для некоторого , и рассмотрим случай . По лемме 1 все вершины 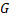являются источниками или найдётся вершина с непустой входящей окрестностью, состоящей из источников. Первая из этих возможностей исключена, поскольку она означает отсутствие дуг в 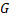. Рассмотрим, таким образом, вершину 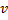с непустой входящей окрестностью , состоящей из источников. В соответствии с определением 4 вершины имеют нулевые веса в графах 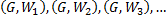, откуда вершина 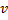имеет нулевой вес в 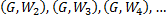. Рассмотрим орграф , такой что 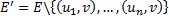. Пусть 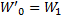– вектор весов 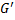, и 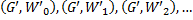– эволюция 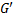. Используя индукцию, нетрудно доказать, что для каждого натурального 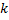выполняется условие 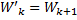. С другой стороны, 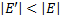, что с учётом предположения индукции даёт 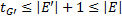, , и