"Возьми вселенную, измельчи её в мельчайший порошок, просей её через мельчайшее сито и потом покажи мне один атом справедливости, одну молекулу милосердия. И всё-таки, — Смерть махнул рукой, — и всё-таки ты действуешь так, будто существует какой-то идеальный порядок в мире, словно есть что-то... какая-то справедливость во вселенной, по которой о ней можно судить". — Тэрри Пратчет, "Санта-Хрякус" (Плоский мир)
В математике есть одна маленькая грязная тайна. Ну ладно, не такая уж она грязная. Но и совсем не маленькая. Она состоит в следующем: В математике всё является делом выбора.
Хотя можно было бы подумать иначе, взглянув на современный учебный план по математике. Каждая теорема доказана, каждая формула сопровождена соответствующими упражнениями, где можно её применить. Пред вами предстаёт длиннющая лестница информации, и вам говорят лезть, лезть, лезть, в конце суля вознаграждение. "Вам пригодится это в реальной жизни!" — говорят они, не сознавая огромность этой лжи – того факта, что большинство образованного населения живёт со "смутными воспоминаниями об уроках математики и ясными воспоминаниями о ненависти к ним".
Нечасто нам объясняют, что все эти вещи абсолютно необязательны — что математика это искусство делать выбор, чтобы знать, каковы могут быть последствия. Что алгебра, исчисление, геометрия это просто слова, которые мы придумали, чтобы сгруппировать вместе наиболее интересные сделанные нами выборы, чтобы выработать исходящие из них наиболее полезные инструменты. Математический акт это игра, сопоставление идей и наблюдение, как они подходят друг к другу. К сожалению это исследование в основном опускается на уроках математики, и вместо этого нам скармливают заранее упакованную и переваренную математическую кашу.
И так же дело обстоит с числами. Мы узнаём о натуральных числах, целых, дробях и наконец, действительных числах. И на каждом этапе мы чувствуем себя обманутыми — нам показали только часть головоломки! Как в конце концов оказалось, существовал "самый лучший", наиболее исчерпывающий, чем все предыдущие, набор чисел, который ждал своего открытия.
Всё время нам казалось, что мы не используем свою интуицию в полную силу. Отрицательные числа помогают нам расплатиться с долгами, дроби помогают честно делить прибыль, а действительные числа помогают нам измерять диагонали и рисовать окружности. Но потом заминка. Если вы удосужились зайти достаточно далеко, вы узнаёте о том, что называют воображаемыми числами, когда кажется, что здравый смысл разбивается на мелкие кусочки. Отрицательные числа здесь могут иметь квадратный корень, уже нельзя сказать, что одно число больше другого, и всё это начинает казаться бессмысленным развлечением людей, которым некуда девать своё время.
Но всё дело в неверном названии. Непонимание возникает по одной простой причине: все числа вымышленные. Нельзя указать на что-либо в мире и сказать: "Вот это 3, а это 5". Можно указать на три яблока, пять деревьев, или на начерченные мелом символы, обозначающие 3 и 5, но концепции 3 и 5, самих чисел, существуют только в нашей голове. Лишь потому, что мы выучили их в таком раннем возрасте, мы этого почти не замечаем.
3 – 5 =?
4/6 =?
√50 =?
√–4 =?
Задачи, требующие от нас изобретения новых чисел, чтобы решать их на системной основе
И когда математики в конце концов столкнулись с числами, которые вели себя чуть иначе, они не могли удержаться, чтобы не назвать их вымышленными или воображаемыми, задав неверный тон следующим поколениям. Ожидания мешали увидеть то, что есть на самом деле, и потребовались десятилетия, чтобы как следует понять результаты.
Теперь эта странность математики известна всем. Воображаемые числа — названные комплексными в сочетании с нашими обычными действительными числами — являются важной частью квантовой физики, электромагнетизма, и многих других областей. Они легко подходят для описания всего, что вращается, волнуется, рябит, сочетаясь или противореча с самими собой или с другими числами. Но именно их уникальная структура позволила Бенуа Мандельброту создать свои великолепные фракталы в конце 70-х, которые поразили всех энтузиастов математики.
И тем не менее, в большинстве случаев к комплексным числам относятся как к неудобству. Поскольку по природе своей они многомерны, они бросают вызов нашим попыткам легко их представить. Графики, описывающие комплексную математику, это обычно лишь упрощённые схематические изображения, только намекающие на то, что происходит за их видимой частью. Поскольку наш мозг по своей природе не может моделировать больше чем 3D, мы можем увидеть лишь срезы гиперпространств, чтобы составить о них какое-то представление. Но не невозможно заглянуть за занавес, и сделав это, можно добыть уникальные прозрения. Всё, что нужно, это готовность выйти за рамки обычных представлений.
Вот о чём эта статья. И запомните урок: комплексные числа это первые типичные числа, которые несомненно странные. Не обращая внимание на надпись "Здесь водятся драконы, оставь все надежды", мы будем исследовать, наслаждаясь чудесными результатами, которые исходят из одного очень простого решения: позволить нашим числам вращаться. Это значит, драконы здесь водятся. Хотя и очень милые.

Фрактал Мандельброта, созданный по простой формуле f(z)=z2+c, где z это комплексное число. Такой тип отношений впервые был изучен Гастоном Джулиа.
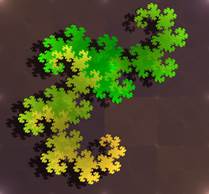
«Кривая Дракона» Хейтуэя, которая имеет удивительную связь с комплексными числами.
Как стрелки часов.
Что значит, позволить числам вращаться? Когда мы делаем математический выбор, нужно быть осторожными. Можно заявить, что 1+1 должно равняться 3, но это только открывает больше вопросов. 1+1+1 равняется 4, 5 или 6? Можно ли вообще создать осмысленную арифметику таким образом? Если нет, что хорошего в этих модифицированных числах? Самое главное, чтобы наши правила были корректными, чтобы они работали. Но если мы просто поменяем местами символы 2 и 3, мы ничего в действительности не изменим в основе математики.
Итак, мы ищем варианты, которые не противоречат с тем, что уже работает, но добавляет что-то новое. Точно так же, как отрицательные числа дополнили положительные, дроби плотно заполнили пространство между ними, а действительные числа каким-то образом втиснулись между последними — нам нужно поискать новые числа там, где пока их нет.
1. Начнём с классической линии натуральных чисел, с отмеченными на ней целыми числами, и поисследуем. Представим, что линия продолжается неограниченно влево и вправо.
2. Здесь возникает проблема с визуализацией: представляя числа как точки, неясно как они взаимодействуют друг с другом. Например, два смежных числа 2+3 в сумме дают 5...
3. Но такая же смежная пара чисел –2 + –1 = –3. Мы не можем легко определить место, где получится красная точка, основываясь на синей и зелёной.
4. Лучше будет представить наши числа, используя стрелки, или векторы. Каждый вектор представляет число через его длину, указывая вправо\влево для положительного\отрицательного направления.
5. У стрелок есть одно хорошее качество: можно изменять их направление, не изменяя их самих. Чтобы сложить две стрелки, нужно просто приложить их концами. И можно легко определить, что –2 + –1 = –3...
6....и точно так же, почему 2+3=5. До тех пор, пока мы верно сохраняем положительные и отрицательные направления, всё отлично работает.
7. Теперь давайте изучим умножение. Начнём с 1 и будем постоянно умножать на 1.5.
8. С каждым умножением вектор увеличивается на 50%. Эти векторы представляют числа 1, 1.5, 2.25, 3.375, 5.0625 – хорошая экспоненциальная последовательность.
9. Теперь будем делать то же самое, только умножать будем всё время на отрицательное число –1.5.
10. Векторы по-прежнему увеличиваются на 50%, но так же переходят на другую сторону, изменяясь с положительного на отрицательный. Эти векторы представляют последовательность 1, –1.5, 2.25, –3.375, 5.0625.
11. Но есть и другой способ взглянуть на это. Что если вместо перехода через ноль от положительного к отрицательному, мы его обойдём, поворачивая вектор по мере его роста?
12. Мы получим те же числа, но откроем нечто замечательное: способ войти в несуществующий мир вокруг числовой линии и пройти через него. Вопрос в том, обоснованно ли это математически, или просто ерунда?
13. Главная проблема в том, чтобы найти систематическое правило для применения этих вращений. Начнём с простой арифметики. Умножение на положительное число не изменяет направления вектора, поэтому мы говорим, что вращаем его на 0º. Умножение на отрицательное число изменяет направление, значит, мы вращаем вектор на 180º. Длины умножаются обычным способом в обоих случаях.
14. Теперь предположим, что мы берём одно из чисел, находящихся в этой несуществующей области, скажем, вектор длиной 1.5, повёрнутый на угол 90º. Что это значит? Именно это мы и хотим выяснить! Мы записываем это как 1.5∠90º (1.5 на угле 90º). Может быть, имеет смысл сказать, что умножение на это число должно повернуть вектор на 90º, увеличив длину снова на 50%.
15. Это создаёт спиральные точки 1∠0º, 1.5∠90º, 2.25∠180º, 3.375∠270º, 5.0625∠360º. Три из них нормальные числа +1, –2.25 и +5.0625, лежащие точно на линии натуральных чисел. Два других – новые числа, появившиеся как по волшебству из пустоты.
16. Давайте подробнее исследуем это вращение. Можно взять 1 на угле 45º. Умножение на единицу не должно изменять длины вектора, что значит, мы получили чистый эффект вращения.
17. Умножая на 1∠45º, можно вращать вектор на сорокапятиградусные интервалы. У нас уйдёт 4 умножения, чтобы от +1 по единичному кругу прийти снова к натуральному числу –1.
18. А это действительно замечательная вещь, поскольку это означает, что наше изобретённое правило создало квадратный корень из –1. Это число 1∠90º.
19. Если мы умножим его само на себя, мы получим угол 90+90=180º, что есть –1 на линии натуральных чисел.
20. Но в действительности то же самое справедливо для числа 1∠270º.
21. Когда мы умножим его само на себя, мы получим угол 270+270=540º. Но поскольку мы обошли вокруг один раз, это то же самое, что угол 180º, поэтому тоже равно числу –1.
22. Либо можно 270º представить как –90º и вращать в другую сторону. Результат будет тот же. Это довольно примечательно: правило остаётся непротиворечивым, не зависимо от того, сколько раз мы обернёмся вокруг.
23. Другими словами, –1 имеет два квадратных корня, разделённых 180º, то есть 1∠90º и 1∠270º. Аналогично тому, как 2 и –2 являются квадратными корнями из 4.
24. Умножение комплексных чисел можно тогда свести к следующему: углы складываются, длины умножаются, с аккуратным соблюдением направления вращения по или против часовой стрелки. Здесь мы умножили два случайных комплексных числа а и b, чтобы получить с.
25. Когда мы начинаем изменять векторы a и b, с изменяется соответственно, следуя за углами a и b. Он вертится вокруг, изменяя свою длину. Таким образом, комплексные числа любят вращаться, и это правило отличает их от обычных векторов.
26. Теперь мы можем представить плоскость комплексных чисел в виде решётки из концентрических окружностей. Окружность единиц, окружность двоек, окружность 1.5 и тд. Каждое число предстаёт в виде множества версий или вариантов – положительное, отрицательное и бесчисленное множество чисел, лежащих между ними, на произвольных углах с обеих сторон круга.
26. Что подводит нас к нашему упорно неуловимому другу i. Это настоящее имя для 1∠90º, а комплексные числа обычно представляют в виде i2= –1. Волшебство состоит в том, что мы можем подставить комплексное число вместо действительного, и всё будет работать, что довольно странно. Для комплексных условий мы получаем комплексные решения.
27. Комплексные числа обычно записываются в виде суммы их (действительной) X координаты и (воображаемой) Y координаты, почти как обычные двухмерные векторы. Но это не совсем верно: уродливое число 3√2+1/2i на самом деле является просто скрытым 1∠30º, и ведёт себя больше как 1, чем как 1/2 или как 3√2. И если знание, как перевести одно в другое, необходимо для реальных вычислений, то можно обмануться, делая это визуально.
28. Но рассматривая отдельные вектора, дальше мы никуда не двинемся. Мы изучаем функции действительных чисел, рассматривая график, который показывает нам каждый результат для каждого аргумента. Чтобы сделать то же для комплексных чисел, мы должны понять, как эти вращающиеся числа, это поле векторов, изменяется в целом.
Замечание: Теперь я помещу +1 или 0º на место двенадцати часов для простоты.
29. Когда мы извлекаем квадратный корень, каждый вектор изменяется. Но в действительности деформируется вся ткань поля комплексных чисел. Каждый круг становится полукругом, потому что все углы делятся пополам – противоположность возведению в квадрат, т.е. удваиванию угла. К длинам применяется обычное правило извлечения корня, сжимая решётку у краёв и растягивая у центра.
30. Но помните, что каждое число имеет два противоположных квадратных корня? Это следует из круговой природы комплексной математики. Если мы возьмём вектор и повернём его на 360º, мы вернёмся в то же место, и два эти вектора будут одинаковыми. Но после деления углов пополам эти два вектора разделены теперь 180º и лежат в противоположных концах круга. В комплексной математике они оба имеют силу.
31. В таком случае операции над комплексными числами похожи на складывание и раскладывание причудливого, растягивающегося и круглого листа бумаги. Это, возможно, трудно уловить, но легче увидеть это в движении. Чтобы помочь увидеть, что происходит, я разрезал диск и отделил положительные углы от отрицательных в 3D.
32. Когда мы возведём в квадрат наши числа, отменяя квадратный корень, углы удваиваются, складывая плоскость внутрь на саму себя. Длины также возводятся в квадрат, восстанавливая размерность решётки.
33. После возведения в квадрат каждый квадратный корень становится поверх своего идентичного близнеца, и мы можем свести всё снова к ровной плоскости. Всё абсолютно совпадает.
34. Таким образом квадратный корень на самом деле выглядит так. Новые числа втекают с "дальнего края", когда мы пытаемся разрезать диск пополам. Плоскость комплексных чисел стремится оставаться непрерывной, и будет складываться и раскладываться, чтобы всегда оставаться таковой. Это одно из замечательных её свойств.
35. У этого складывания и раскладывания нет пределов. Если мы возведём каждое число в четвёртую степень, углы увеличатся вчетверо, а длины возводятся в четвёртую степень. Это приведёт к 4 копиям плоскости, сложенным в одну.
36. Однако, не всегда всё так точно совпадает. Что будет, если мы возведём всё в иррациональную степень, скажем √1/2? Углы умножаются на 0.707106..., что означает, что поворот на 360º теперь стал 254.56º.
37. Поскольку ни один из множителей 360 не делится на √1/2, наша решётка никогда не совпадёт сама с собой снова, не зависимо от того, как далеко мы её будем продолжать. Таким образом, эта операция делит одно единственное комплексное число на бесконечное количество отдельных копий.
38. Для каждой иррациональной степени p существует бесконечное количество решений zp=c, и все они лежат на круге. Чтобы попробовать понять, почему это так, мы можем взглянуть на ряд Тейлора: произвольная функция f(z) может быть записана в виде бесконечной суммы a+bz+cz2+dz3+... Если z комплексное, то эта сумма не просто представляет собой конечное количество складываний, но умопомрачительное бесконечное оригами комплексного пространства.
Мы увидели, что комплексные числа это стрелки, которые любят вращаться, и которые могут вести себя как числа: их можно складывать и умножать, так как для этого можно найти систематическое правило. Мы также увидели, на что похожи степени комплексных чисел: мы складываем или раскладываем всю плоскость путём умножения или деления углов, одновременно возводя в степень их длины.
Вытаскиваем дракона из шляпы
С основным пониманием, что такое комплексные числа и как они двигаются, мы можем начать строить фракталы Джулиа.
В их основе лежит следующая функция: f(z)=z2+c
Это значит: отметить на плоскости квадрат комплексного числа z, а затем прибавить к этому постоянное число. Чтобы сгенерировать фрактал Джулиа, нужно применить эту формулу многократно, каждый раз подставляя новый результат в функцию zn+1=(zn)2+c
Мы хотим изучить, как изменяется zn, если мы подставим различные начальные значения z1, и будем повторять n раз. Итак, давайте попробуем и посмотрим, что получится.
1. Наша область исследования – диск комплексных чисел длиной меньше 2-х. Я выделил круг единиц как базовый.
2. Возьмём произвольный набор чисел, как эта сетка, и начнём применять к каждому из них формулу f(z)=z2+c. Вместо векторов я нарисую просто точки, чтобы не засорять диаграмму.
3. Сперва каждое число мы возведём в квадрат. То есть удвоим их углы и возведём в квадрат их длины. Возведение в квадрат имеет двойной эффект: числа больше единицы увеличиваются и выталкиваются наружу решётки, а числа меньшие единицы уменьшаются и втягиваются внутрь.
4. Затем снова восстановим нейтральное состояние решётки, оставляя числа на их новых местах. Также выберем случайную величину для константы, к примеру 0.57∠59º.
5. Теперь добавим c каждой точке, завершая один цикл итерации Джулиа, f(z)=z2+c. В результате некоторые числа стали ближе к источнику (к нулю), другие дальше. Комбинация складывание плюс сдвиг произвела не очень заметный эффект на числа.
6. Начнём вторую итерацию и снова возведём в квадрат каждое число. Числа, лежащие вне ключевого круга единицы в центре, снова вытолкнутся. Другие числа продолжат стягиваться к центру.
7. Если мы возьмём более общий план, мы увидим, как большие числа спиралью уходят прочь и исчезают совсем. Небольшое подспорье в виде с недостаточно, чтобы их вернуть.
8. Остальные остаются в центре, втягиваясь всё больше, но они так же рискуют быть вытолкнутыми из круга из-за с.
9. Снова приводя решётку в нейтральное состояние, в конце мы добавляем то же значение с нашим векторам. После этого шага наша первоначальная сетка из чисел превратилась в кучу-малу.
10. Если мы продолжим этот процесс, останутся ли какие-либо числа в центре? Или они все в конце концов будут выброшены за пределы круга? К несчастью, очень трудно увидеть, что будет происходить, продолжая итерации, потому что мы теряем след, откуда пришла каждая точка.
11. Поэтому вместо этого мы пойдём в обратном направлении. Мы установим «безопасную зону» из всех чисел меньше двух, формируя жёсткий диск из тех чисел, которые не будут потеряны безвозвратно. Мы хотим знать, откуда все эти числа могут появляться. Чтобы облегчить слежение за этими точками, я раскрасил одну область в другой оттенок.
12. Сперва мы должны снова произвести над числами действие, но на этот раз в обратном направлении – вычесть с.
13. Теперь извлечём квадратный корень, чтобы найти zn-1=+\–√(zn – c), что есть итерация Джулиа наоборот.
14. После одной итерации назад диск сплющится наклонный в овал. Все эти точки определённо останутся в центре после одной итерации.
15. Когда мы применим вторую итерацию, рисунок начнёт развиваться. Повторным разворачиванием мы создали две выпуклости там, где прежде была всего одна.
16. В то же время квадратный корень изменяет длину каждого числа. В результате мы сжимаем рисунок радиально, уменьшая в размере начальные его элементы, и сочетая их с вновь созданными.
17. После 4 итераций мы начинаем замечать намёки самоподобия. Рукава рисунка разветвляются спиралями.
18. Но всё, что мы сделали, это выбрали синюю безопасную зону, чтобы она включала только те точки, которые выживут до пятой итерации.
19. Замечательно то, что фрактал, похоже, искажается равномерно: выделенные нами круги не вытягиваются в овалы. Это не совпадение. Комплексные операции действительно очень устойчивы в том отношении, что они всегда и везде сохраняют углы. Для этого построение диаграммы должно действовать как чистое изменение размера и вращение каждой точке, без отсекания какой бы то ни было части. Это позволяет фракталу быть идентичным себе в различных масштабах.
20. Перескочив до 12-й итерации мы определённо покинули царство точной традиционной геометрии. Несмотря на дикую извилистость общая карта z12 всё же имеет свойство равномерности, которая называется конформным преобразованием.
21. После 128 итерации у нас получилась замысловатая похожая на дракона форма, приближая безопасную зону к истинной карте фрактала z ∞. Числа, которые составляют голубую область, это самые стойкие точки, которые переживут ещё 128 покушений на их жизнь. Все остальные определённо вылетят прочь.
22. Эта сложная форма является результатом простого многократного складывания с добавлением константы в промежутках. Если мы будем делать итерации Джулиа вперёд, то есть возводить в квадрат и сдвигать, то мы увидим, как эта форма совпадает сама с собой и выглядит идентично до и после.
23. Для различных значений c фрактал видоизменяется в другие формы. Можно обнаружить буквально бесконечное их разнообразие. Некоторые фигуры состоят из раздельных частей. В этом случае \ с \ достаточно большое, чтобы вытеснить твёрдый диск вон из центра за одну итерацию, но не настолько далеко, чтобы некоторые точки не вернулись обратно внутрь. Если \ с\ будет намного больше, фигура исчезнет.
24. Для меньших с фракталы Джулиа целостны. Даже небольшое изменение значения с может привести к сильным отличиям. Здесь мы ZONE IN ON какие-то пушистые облачка прямо за границей «сплошной зоны». Довольно странно, что когда с не находится внутри своей фигуры Джулиа, набор не сплошной. Заметьте, что в данном случае 128 итераций не достаточно: остаются большие сплошные области, которые будут разорваны при дальнейших итерациях.
25. Эта площадь фрактального пространства создала Долину Морских Коньков, по довольно очевидным причинам.
26. Неподалёку мы нашли эти похожие на драгоценные камни спирали.
27. Существует множество замечательных комбинаций форм, спрятанных глубоко внутри, как это жемчужное ожерелье, укрытое в чём-то напоминающем пальмы.
28. Мы даже можем создавать снежинки. Разительные перемены из-за с раскрывают хаотическую природу фракталов. Математически хаос определяется тем, что даже самое незначительное изменение может накопить и вызвать непредсказуемо большой эффект.
29. Если мы изменим нашу формулу итерации, например, до четвёртой степени f(z)=z4+c, изменится вся форма. Поскольку каждая итерация теперь делит один бугорок на четыре, в результате форма будет иметь четверную круговую симметрию.
30. И опять, различные значения с создают различные формы, вызывая разительные изменения.
31. Чтобы понять эффект с, мы должны построить фрактал Мандельброта. Он похож на Джулиа, только формула применяется по-другому. Мы будем снова использовать z2+c. Вместо различных начальных значений z1, мы будем выбирать каждый раз различные значения c, а начинать будем с z1=0. Поскольку c это больше не константа, формирование диаграммы перестаёт быть простой операцией складывания. Каждая итерация теперь уникальна и не так легко визуализируется.
32. Поскольку фрактала Мандельброта покрывает своей поверхностью все возможные значения с, он содержит в себе часть каждого соответствующего фрактала Джулиа. В окрестностях любого с он выглядит как фрактал Джулиа, у которого эта величина является константой. Здесь мы движемся в направлении трёхстороннего креста внизу фрактала Мандельброта. Такие же признаки развиваются в фрактале Джулиа.
33. Там, где фрактал Мандельброта круглый и выпуклый, такой же и фрактал Джулиа.
34. Спирали и морские коньки из предыдущих фракталов встречаются и здесь. Можно буквально увидеть эти формы с обеих сторон долины, развивающиеся в направлении конских голов и спиралей соответственно. Но фрактал Мандельброта действует как карта для фракталов Джулиа в гораздо более прямом смысле: везде, где фрактал Мандельброта закрашен (синим), соответствующий фрактал Джулиа также сплошной. Белые области это такое значение с, которое создаёт разорванные фракталы Джулиа.
35. То, что фрактал Мандельброта это точная до пикселя карта фракталов Джулиа, наводит на мысль о том, что они оба на самом деле являются сечениями одного объекта более высокой размерности. Рассматривая эти сечения по мере их обхода, мы можем получить неясное представление о его форме и сложности. В этом объекте каждая точка фрактала Мандельброта связана с центром соответствующего фрактала Джулиа. И не так-то легко представить себе этот 4D объект.
36. Но, как и все фракталы, фрактал Мандельброта содержит в себе копии себя самого, спрятанные в его кромке. Это лишь одна из множества различных копий. В результате при большом приближении фрактала Мандельброта можно достигнуть потрясающих уровней красоты и сложности. Лучше всего это делать в специальной программе, которая может вычислять с точностью до сотен цифр после запятой.
Строить фракталы это, вероятно, самое бесполезное, но бесспорно очаровательное применение комплексной математики. Оно также раскрывает уникальные свойства комплексных операций, как конформное преобразование, что обеспечивает определённую строгость результату.
Однако, чтобы найти практическое применение комплексной математике, мы должны выяснить, как привязать её обратно к реальному миру.
Неподвижное движение
Хорошо, что нам не надо далеко за этим ходить. Когда мы описываем волнообразный феномен, звук ли это, электричество, или субатомные частицы, нам так же интересно, как волна развивается и изменяется. Комплексные операции больше всего подходят для этого, поскольку они естественным образом происходят из кругов. Противоположные числа могут взаимно нейтрализоваться, числа одного направления будут усиливать друг друга – точно как ведут себя при встрече две волны. И путём складывания или раскладывания мы можем изменить частоту системы – удвоить её, уполовинить, или изменить как угодно.
Более сложные операции используются, например, для моделирования электромагнитных волн, будь то радио, пакеты WiFi или потоки ADSL. Это требует точного контроля частот, которые ты генерируешь или принимаешь. Делать это без комплексных чисел, ну, просто геморрой. Поэтому, зачем использовать нудные действительные числа, когда комплексные числа могут сделать за тебя всю работу?
1. Возьмём для примера синусоиду w(x).
2. Поскольку волна распространяется в пространстве, её значения должны колебаться во времени. Скорость изменения во времени указана наверху. Это вертикальная скорость в каждой точке. Как волна, так и скорость её изменения, подвержены сложному числовому танцу.
3. Но чтобы должным образом описать это движение, мы должны опуститься ещё на уровень глубже. Мы должны изучить скорость изменения вертикальной скорости волны. Это её вертикальное ускорение. Мы видим, что зелёные векторы тянут за собой синие векторы, а синие векторы тянут за собой волну.
4. Чтобы легче увидеть, что происходит, мы поместим векторы в центре. Ускорение оказывается одинаковым, но противоположным самой волне.
5. Но это просто счастливое совпадение. Если мы сдвинем волну вверх на одну единицу, её противоположность сдвинется вниз на одну единицу. Но её скорость и ускорение останутся неизменными. Следовательно, ускорение это не просто противоположность волны.
6. На самом деле происходит то, что зелёные векторы совпадают с изгибами волны, положительные во впадинах, отрицательные на вершинах. Интуитивно это можно объяснить так, что волна стремится занять среднее положение: это вытаскивает её вверх из впадин и тянет вниз с вершин.
7. Но кривизна это скорость изменения наклона, а наклон это изменение в пространстве. Поэтому чтобы описать реальную волну, мы должны установить связь между изменениями во времени «второго уровня» и изменениями положения в пространстве, всё дважды продифференцировав. Это Сложно с большой буквы.
8. Но давайте попробуем это сделать с помощью комплексных чисел. До сих пор у нас был двухмерный график, показывающий реальную величину волны в реальном пространстве. Теперь сделаем величину волны комплексной. На диаграмме обозначены 1D (расстояние) и 2D (функция волны), значит нам нужна 3D диаграмма.
9. Комплексную плоскость мы расположим на старой оси Y (реальной) и новой оси Z (воображаемой).
10. Чтобы построить комплексную волну, мы делаем с комплексными числами то, что у них получается лучше всего: мы заставляем их вращаться и закручиваться в спираль. В этом случае наша волновая функция это просто различные 1∠ x – постоянная длина, равномерно вращающаяся и перемещающаяся в пространстве.
11. Чтобы заставить волну двигаться, мы должны просто скручивать её на месте. Что, как мы теперь знаем, то же самое, что просто умножить на возрастающий угол 1∠ t. Если мы начертим комплексную скорость каждой точки, на первый взгляд может показаться, что это ничуть не проще, чем реальная волна. Но фактически эти векторы совсем не меняют свою длину, в отличии от их реальной версии. В то время, как векторы скорости тянут за собой волну, оба они подвергаются чистому вращению.
12. В каждый момент времени скорость отстоит от самой волны на угол 90º. А это значит что описанные в комплексных числах волновые уравнения супер просты. Вместо двух производных, то есть скорость изменения скорости, нам нужна только одна. Есть прямые отношения между значением и скоростью его изменения. Необходимый угол поворота на 90º может быть записан просто как умножение на i.
13. Чтобы восстановить реальную волну из комплексной, мы можем просто спроецировать её обратно на плоскость, опуская воображаемую часть. Используя комплексные числа для описания волны, мы позволяем им вращаться на месте, не изменяя амплитуды, что оказывается намного проще.
14. По сути это проецирование волны на плоскость имеет совершенно разумную комплексную интерпретацию: так происходит, когда мы вычисляем среднюю величину волны, вращающейся против часовой стрелки (положительная частота), и волны, вращающейся по часовой стрелке (отрицательная частота). Скручивая их обе в противоположных направлениях, мы получаем движущуюся комбинированную волну, привязанную к оси действительных чисел.
15. Но если мы добавим две произвольные комплексные частоты, их сумма тут же превращается в спирографический узор, который способен развиваться и распространяться, даже просто вращаясь на месте. Хотя изначальные волны имеют постоянную амплитуду равную 1, относительная разница углов (т.е. фаз) при их сокращении приводит к удивительным результатам.
16. Изгибы на самом деле так же не двигаются вперёд: они просто крутятся на месте, так или иначе создавая движение. В действительности именно так выглядит квантовая суперпозиция, где две или больше комплексных вероятностных волны сочетаются и сталкиваются. Где в результате получается ноль, там две отдельные возможные состояния нейтрализуют друг друга, создавая интерференцию. То, что лежащие в основе всего этого числа, являются комплексными, не мешает им описывать реальную физику, и фактически, похоже, так в действительности работает природа.
17. Этот пример чётко демонстрирует фазовый вихрь. Мы можем начертить скорость двух частот и их комбинацию в уменьшённом масштабе для ясности. И опять здесь видна сила описания волны с помощью комплексных чисел, что позволяет вам разделить сложное движение на простые повторяющиеся вращения... на числа, которые любят вращаться.
Конец это только начало
В визуализации комплексных волн мы увидели функции, которые могут переводить действительные числа в комплексные и обратно. Эти функции можно легко изобразить на 3D диаграммах от действительных чисел к комплексным или наоборот. Ты пересекаешь одно реальное измерение двумя измерениями комплексной плоскости.
Но комплексные операции в основном работают от комплексных чисел к комплексным. Чтобы увидеть это, к несчастью, вам потребуются четырёхмерные глаза, которые природа ещё не придумала. Есть способы спроецировать эти графики на 3D, которые вроде бы имеют смысл, но всегда очень непросто их интерпретировать.
На каждую математическую концепцию, которую мы способны воспринять непосредственно, существует бесчисленное количество тех, которые мы не можем легко вообразить. Это проклятье математики, но в то же время её очарование.
Поэтому, я старался придерживаться вещей, которые (относительно!) легко себе представить. Если будет интерес, будущий пост может охватить тему о природе eix, трансформации Фурье, что-то из современной квантовой механики и тд.
Пока история окончена. Надеюсь, мне удалось зажечь несколько лампочек там и сям, и что вы получили удовольствие, читая это, как и я, когда писал.
https://acko.net/blog/how-to-fold-a-julia-fractal/